SOME RESULTS OF STUDIES ON ECLIPSING VARIABLES 
                    by S. PIOTROWSKI, Warsaw


    The present communication deals with certain results of studies on 
eclipsing variables conducted in the Warsaw Observatory.
    In the years 1947-48 I worked out^1 an analytical method of determining 
the intermediary orbit of an eclipsing system. It is characteristic for this 
method that from the first beginning we apply the fundamental equation 
of the problem to individual normal points and we do not use the free-hand 
curve at all. It is because of the mentioned character of the method that we 
are able to weight in a rational way individual equations and we obtain the 
elements of the system with their mean errors using the least squares  
algorithm. In this way we get from the outset an insight into the determinacy 
of the problem; moreover we can judge whether the degree of approximation 
is sufficient for applying the - rather laborious - method of differential 
corrections. The method I am speaking of was applied several times by  
different authors - most often in the form and with modifications given by Z. 
Kopal in his monograph "The Computation of Elements of Eclipsing Binary
Systems"^2.
    In the last months we applied in Warsaw this method - together with 
the method of differential corrections in the final stage - to the eclipsing 
system WW Aur. Our results must be still regarded as preliminary. The 
observational material consisted of photoelectric observations in two colours 
executed with the photometer with the 1P21 cell of the Cracow Observatory. 
The observations were executed by myself and my collaborators (in the first 
place A. Strzalkowski) in Cracow; the reductions and computations were 
performed in Warsaw by K. Serkowski and B. Jun.
    We had at our disposal more than 1500 sets obtained in the years 
1948-51 during 33 evenings. Each set consists of 4 readings of the galvanometer 
on the variable star (2 through the yellow filter and 2 through the violet 
one) plus 4 analogical readings on the comparison star plus galvanometer 
readings of the dark current and of the sky background (in yellow and violet). 
There is a certain pecularity in the manner in which the individual sets were 
grouped into "supersets" called observations. We had namely divided the 
light curve in equal intervals of 0.004p (it is nearly 0.01d) and from all 
sets (on the average 3) from the same night falling in the given interval one
observation was formed. Nearly 500 observations in each colour were obtained 
- and these observations will be published.^3 Observations from different
nights and pertaining to the same phase-interval were afterwards grouped into
normal points. Outside eclipses the intervals were taken of course greater. 
    The light curve shows two minima of nearly equal depth (about 0.7m); 
there is a small ellipticity (the coefficient of cos^2 theta in light units 
being 0.014) and no observable reflection. Though both components are of the
same spectral type (A7) variations of colour index are clearly visible in the 
primary minimum: the star is growing redder at mid-eclipse by about 0.05m; 
no variations are detectable in the secondary minimum. There is one interesting 
feature of the curve of colour variations: just after the beginning and just 
before the end of the primary minimum the star is bluer than outside eclipses.
It is worth-while noticing that the same is true for the system U Oph according 
to photoelectric observations of N. L. Magalashvili.^4


 

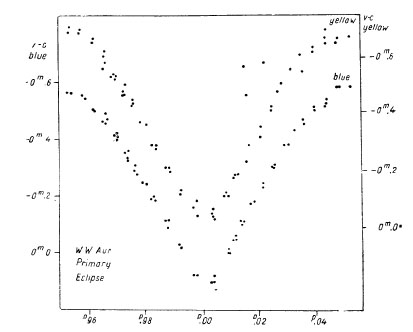               Fig. 1. WW Aur. The light curve in primary minimum


  Few years ago the light variations of WW Aur were observed photoelectrically 
(but without filters) by C. M. Huffer and the elements of the 
system were determined by Z. Kopal.^5 It is recomforting to see that the 
system of elements determined by Kopal differs but little from our system, 
though the observational evidence on which the computations of American 
authors are basing is in one respect essentially different from Warsaw data. 
The point is that Kopal used when determining the elements the ratio of 
brightnesses of both components obtained by R. M. Petrie^6 from spectroscopic 
observations. Our analysis of Petrie's determination convinced us that his 
value of L_a/L_b is not reliable and thus in Warsaw we have used only our own 
photometric data. Though the rejection of spectroscopic observations  
considerably diminished the determinacy of the problem (one may notice that 
Kopal had from the first beginning a practically fixed value for L_a/L_b - and 
in consequence, for k) our results concerning the geometric elements of the
system agree rather well with those of Huffer and Kopal (the greatest  
difference is of course in k).
   Perhaps the most valuable result of our computations is the relatively  
well determined value of the difference of limb darkening coefficient in the  
violet and yellow light (approx. 4200 A and 5300 A). The assumed, starting  
value of this coefficient, common for both components and both colours
was 0.6; the difference came out 1/2 Delta u = 0.09+-0.03, the star discs 
being more darkened in violet light.

 

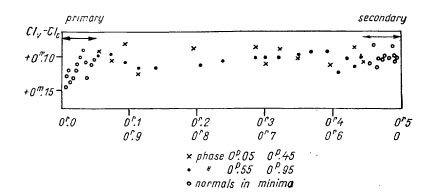       Fig. 2. WW Aur. The curve of colour variations

In the end of my communication I would like to point at one fact concerning 
not the system WW Aur itself but the algorithm employed. The values  
of the elements obtained during the intermediary orbit determination and  
these computed by the method of differential corrections agree satisfactorily;  
the same is not true for mean errors obtained in both stages of computation.  
I know from private communications (in particular from Z. Kopal) that the  
same fact was noticed by other computers. So this point needs an elucidation.

       Budapest, August 1956.

 1 Ap. J., 106, 472; 108, 36; 108, 510.
 2 Harvard Observatory Monographs No. 8, 1950.  
 3 Acta Astronomica, Vol 6 (in press).  
 4 Abastumani Bull., 10, 21, Table VI, 1947.  
 5 Ap. J., 114, 297, 1951.
 6 Publ. Dom. Ap. Obs. Victoria, 7, 205, 1939.