Non-Periodic Phenomena in Variable Stars
IAU Colloquium, Budapest, 1968
STATISTICAL AND PHYSICAL INTERPRETATION OF NON-PERIODIC
PHENOMENA IN VARIABLE STARS
Introductory Report by
L. DETRE
Konkoly Observatory, Budapest
The subject of this Colloquium is similar to that of the third IAU
Symposium on Non-Stable Stars, held 13 years ago in Dublin. At that
time, the subject was limited to certain areas of particular interest.
Now, we are trying to pay attention to the complex of non-periodic
phenomena in variable stars. Dr. Herbig (1968), in his announcement of
this Colloquium, has given an excellent summary of the topics in which
we are concerned in these days.
Since then, the pulsating radio sources are added to our field, as they
are most likely stars and they show in the amplitude of the pulses
random fluctuations, that according to recent spaced receiver
observations by Australian radio astronomers (Slee et al. 1968) take
their origin predominantly at or near the sources themselves, and not in
the intervening interplanetary or interstellar media.
Not long before, it was generally believed that stellar variability is
only significant, if the variation exhibits a sizeable amplitude and
(or) a certain amount of regularity. We shall adopt a different
approach: random phenomena occurring both in variable and non-variable
stars are of the same importance as regular large-scale phenomena, not
only in the case when they result in such spectacular events as
eruptions of novae or novoids, stellar flares, or the phenomena
connected with the R Coronae Borealis stars, but also when they appear
as small changes in the shape or position of spectral lines or in the
periods of periodic variables, because these minute effects might be the
manifestations of fundamental hydrodynamic or magnetic circulations in
the star or signs of a star's rotational instability. In this way the
frequency, intensity, or extent of random stellar phenomena may show
cycles or pseudoperiods, as for example the solar magnetic activity with
all its random manifestations like spots, plages, prominences and
flares, has a 22 year cycle, and the irregular velocity and brightness
oscillations in the photosphere of the sun have a pseudo-period of about
5 minutes. Other periodicities may sometimes be imposed on the
observable effects of stellar random phenomena by stellar rotation,
binary motion, or by some interaction with pulsation.
Any observed data representing a physical phenomenon, e.g. a light curve
or radial velocity curve of a variable star, can be classified as being
either deterministic or nondeterministic. Deterministic data can be
described by an explicit mathematical relationship. They are either
periodic or nonperiodic. The simplest periodic phenomenon has a
sinusoidal time history and a frequency spectrum (that is an
amplitude-frequency plot) consisting of a single frequency. Generally
the spectrum of periodic data contains besides a fundamental
frequency, f, its multiples. Almost periodic data, when the effects of
two or more unrelated periodic phenomena are mixed, can be similarly
characterized by a discrete frequency spectrum. For the determination of
these frequencies different methods of harmonic analysis can be applied.
For transient nonperiodic data, as e.g. the light curve of a flare, a
discrete spectral representation is not possible. However, a continuous
spectral representation can be obtained from a Fourier integral given by
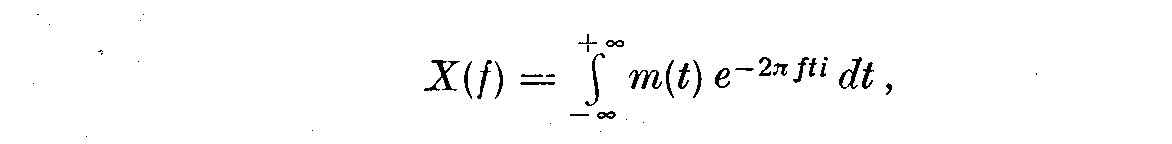 (1)
where m(t) is the light curve, X (f) is the Fourier spectrum.
We can consider irregular stellar variability as the observable effect
of random succession of transitory events. On the sun and some types of
variable stars, e.g. novae, U Geminorum, R Coronae Borealis and flare
stars, these events can be observed separately. Solar activity can be
followed even spatially separated. But generally, only the intermingling
of many local and global transitory events can be observed in the stars
as a continuously varying irregular light curve.
Also such a random time series m = m(t) can be represented by a
complicated mathematical relationship over a time interval (0, T). But
the formula will not hold for t > T. We obtain for different time
intervals different formulae, different sample records of the same
random process. Therefore, it is more practical to characterize a random
time series by some simple parameters:
1. Taking the mean value of m for a time interval (0, T)
(1)
where m(t) is the light curve, X (f) is the Fourier spectrum.
We can consider irregular stellar variability as the observable effect
of random succession of transitory events. On the sun and some types of
variable stars, e.g. novae, U Geminorum, R Coronae Borealis and flare
stars, these events can be observed separately. Solar activity can be
followed even spatially separated. But generally, only the intermingling
of many local and global transitory events can be observed in the stars
as a continuously varying irregular light curve.
Also such a random time series m = m(t) can be represented by a
complicated mathematical relationship over a time interval (0, T). But
the formula will not hold for t > T. We obtain for different time
intervals different formulae, different sample records of the same
random process. Therefore, it is more practical to characterize a random
time series by some simple parameters:
1. Taking the mean value of m for a time interval (0, T)
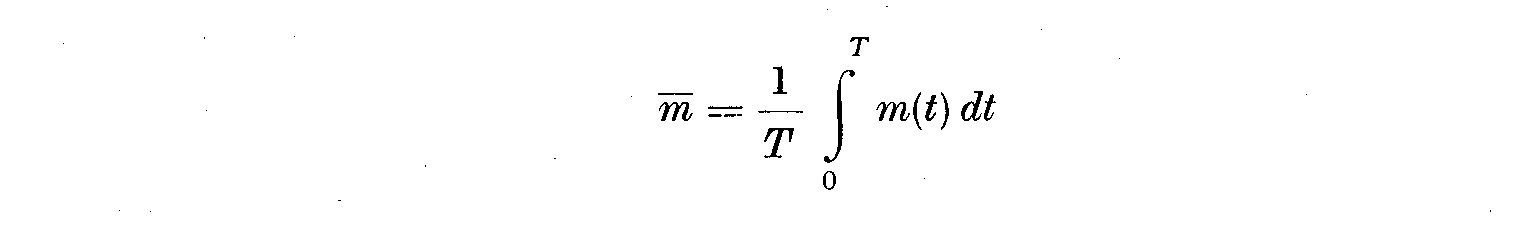 (2)
and putting mean(m) = 0 we can define the variance, as the mean square value
about the mean, by
(2)
and putting mean(m) = 0 we can define the variance, as the mean square value
about the mean, by
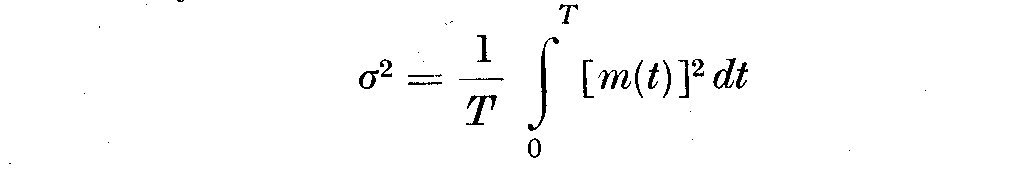 (3)
The positive square root of the variance is called the standard deviation.
2. The probability density function describes the probability that the
data will assume a value within some defined range at any instant of
time. The probability that m(t) assumes a value within the range between
m and m + Delta m may be obtained by taking the ratio T_(m, m + Delta m) / T ,
where T_(m, m + Delta m) is the total amount of time that m(t) falls inside
the range (m, m + Delta m) during an observation time T.
3. The autocorrelation function describes the general dependence of the
values of the data at one time on the values at another time. An
estimate for the autocorrelation between the values of m(t) at times t
and t + tau may be obtained by taking the product of the two values and
averaging over the observation time T. In equation form:
(3)
The positive square root of the variance is called the standard deviation.
2. The probability density function describes the probability that the
data will assume a value within some defined range at any instant of
time. The probability that m(t) assumes a value within the range between
m and m + Delta m may be obtained by taking the ratio T_(m, m + Delta m) / T ,
where T_(m, m + Delta m) is the total amount of time that m(t) falls inside
the range (m, m + Delta m) during an observation time T.
3. The autocorrelation function describes the general dependence of the
values of the data at one time on the values at another time. An
estimate for the autocorrelation between the values of m(t) at times t
and t + tau may be obtained by taking the product of the two values and
averaging over the observation time T. In equation form:
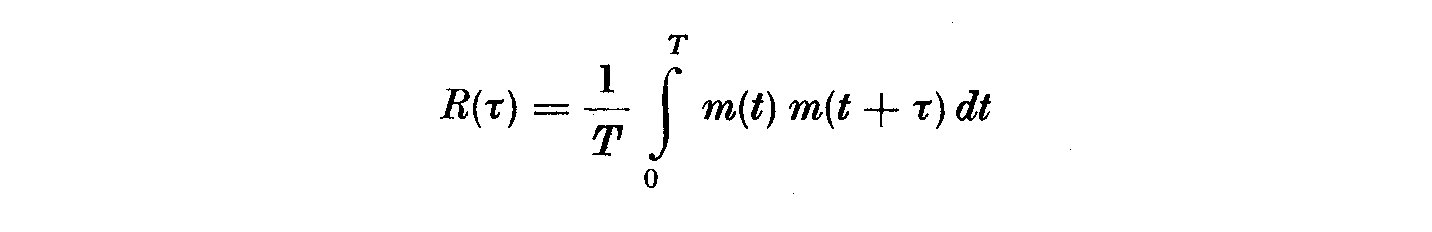 (4)
R(tau) is an even function with a maximum at tau = 0.
4. For stationary data, i.e. for data characterized by time-independent
parameters, we can construct the Fourier transform of the autocorrelation
function
(4)
R(tau) is an even function with a maximum at tau = 0.
4. For stationary data, i.e. for data characterized by time-independent
parameters, we can construct the Fourier transform of the autocorrelation
function
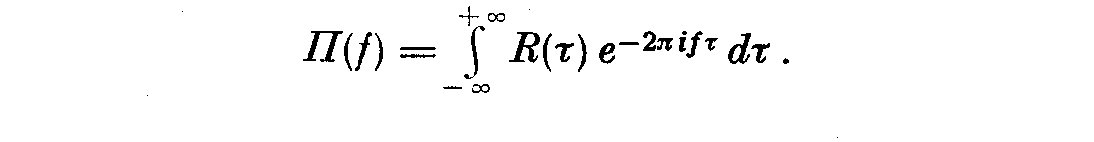 (5)
Pi(f) is called the power spectral density function. That is a breakdown of the
light curve into sinusoidal components and gives the mean squared amplitude
of each component.
In the first column of Fig. 1. we see four special light curves, a sine
wave (a), a sine wave with superposed irregularity (b), a narrow-band random
light curve having cycles of nearly equal length (c), and a wide-band random
light curve with strongly different cycles (d).
In the next column of Fig. 1. we see the corresponding probability density
function plots. For the sine wave we have the maxima for p(m) at the
extremities, because the curve varies slowly there.
Next to the right we see the autocorrelograms. The sharply
peaked autocorrelogram diminishing rapidly to zero (d) is typical of
wide-band random data with a zero mean value. The autocorrelogram for
the sine wave with random noise is simply the sum of the
autocorrelograms for the sine wave and random noise separately (b). On
the other hand, the autocorrelogram for the narrow-band random light
curve appears like a decaying version of a sine wave autocorrelogram.
Finally we see the corresponding power spectra. A discrete power
spectrum for a sine wave and a relatively smooth and broad power
spectrum for the wide-band random light curve. The power spectrum for
the sine wave with irregularities is the sum of the power spectra for
the sine wave and the random case separately. On the other hand, the
power spectra for the narrow band random light curve is sharply peaked,
but still smoothly continuous as for random light-curve. The period
corresponding to the peak may be called as pseudo-period. The four
examples illustrate a definite trend in all the three parameters going
from the sine wave to the wide-band noise case.
The principal application for an autocorrelation and for a power spectral
density function is the detection of periodicities which might be masked in a
random background. Any periodicity in the light variation will manifest
itself as a series of peaks corresponding to a fundamental and its
harmonics.
Such method of analysis requires enormous amount of computation,
hence it has not been popular in the past. With the aid of high speed
computers this is no longer a problem. However, the requirements
of accuracy, extent, continuity, and reasonable homogeneity for the light
curve to be analysed restrict considerably the applicability of the method
to semiregular or irregular variable stars. Only one single semiregular
variable was till now treated by this way, mu Cephei, on the one hand
by Ashbrook, Duncombe and Woerkom (1954), who found the light curve to result
from stochastic rather than harmonic processes, on the other hand by Sharpless,
Riegel and Williams (1966) with the conclusion that the light variations are
characterized by a much greater degree of regularity than is generally
attributed to stars classed as semiregular variables.
(5)
Pi(f) is called the power spectral density function. That is a breakdown of the
light curve into sinusoidal components and gives the mean squared amplitude
of each component.
In the first column of Fig. 1. we see four special light curves, a sine
wave (a), a sine wave with superposed irregularity (b), a narrow-band random
light curve having cycles of nearly equal length (c), and a wide-band random
light curve with strongly different cycles (d).
In the next column of Fig. 1. we see the corresponding probability density
function plots. For the sine wave we have the maxima for p(m) at the
extremities, because the curve varies slowly there.
Next to the right we see the autocorrelograms. The sharply
peaked autocorrelogram diminishing rapidly to zero (d) is typical of
wide-band random data with a zero mean value. The autocorrelogram for
the sine wave with random noise is simply the sum of the
autocorrelograms for the sine wave and random noise separately (b). On
the other hand, the autocorrelogram for the narrow-band random light
curve appears like a decaying version of a sine wave autocorrelogram.
Finally we see the corresponding power spectra. A discrete power
spectrum for a sine wave and a relatively smooth and broad power
spectrum for the wide-band random light curve. The power spectrum for
the sine wave with irregularities is the sum of the power spectra for
the sine wave and the random case separately. On the other hand, the
power spectra for the narrow band random light curve is sharply peaked,
but still smoothly continuous as for random light-curve. The period
corresponding to the peak may be called as pseudo-period. The four
examples illustrate a definite trend in all the three parameters going
from the sine wave to the wide-band noise case.
The principal application for an autocorrelation and for a power spectral
density function is the detection of periodicities which might be masked in a
random background. Any periodicity in the light variation will manifest
itself as a series of peaks corresponding to a fundamental and its
harmonics.
Such method of analysis requires enormous amount of computation,
hence it has not been popular in the past. With the aid of high speed
computers this is no longer a problem. However, the requirements
of accuracy, extent, continuity, and reasonable homogeneity for the light
curve to be analysed restrict considerably the applicability of the method
to semiregular or irregular variable stars. Only one single semiregular
variable was till now treated by this way, mu Cephei, on the one hand
by Ashbrook, Duncombe and Woerkom (1954), who found the light curve to result
from stochastic rather than harmonic processes, on the other hand by Sharpless,
Riegel and Williams (1966) with the conclusion that the light variations are
characterized by a much greater degree of regularity than is generally
attributed to stars classed as semiregular variables.
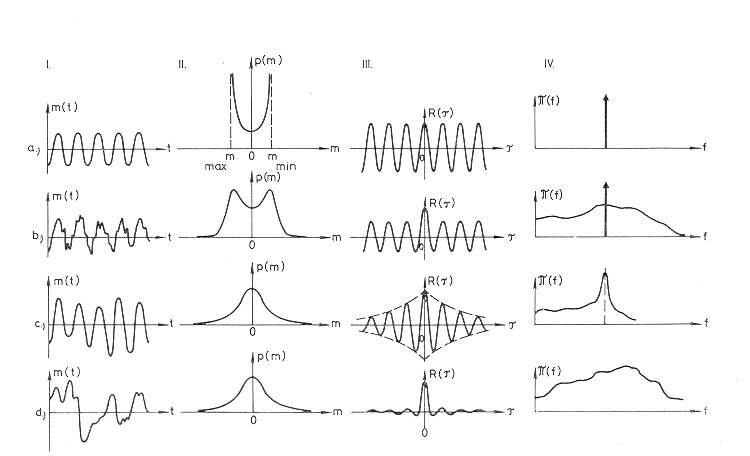 Fig. 1. Light curves, corresponding probability density functions,
autocorrelograms and power spectra (s. text).
Lukatskaya (1966) has investigated the autocorrelation and spectral functions
of seven T Tauri-type variables and those of AE Aqr (1968), Kurochkin (1962)
those of T Orionis, and on this colloquium we shall hear Dr. Plagemann
on the same topic.
A very important question is, are the parameters of the light curves of
irregular variables constant in time, or are they changing. Tsessevitch and
Dragomineskaya (1967) investigated the light variation of 10 RW Aurigae stars
on sky patrol photographs of the Odessa, Harvard, Dushanbe and Sonneberg
observatories. They prepared probability density functions for several stars,
finding longterm variations of this function, with cycles of 25 to 60 years.
Hence, light curves of some irregular variables represent nonstationary data.
A particular random process is the so called Markov process. The property
that distinguishes Markov processes from more general random ones can be
described in non-mathematical form like this: If we know the present state of
the process, and want to make predictions about its future, then information
about the past has no predictive value, i.e. the process has no memory, its
relationship to the past does not extend beyond the immediately preceding
observation. We have a beautiful example for Markov processes in astronomy,
the O-C diagrams for periodic variables, if the period or phase fluctuations
are random, and independent from the preceding ones.
If we are able to determine the length of many individual cycles of a
variable star, as for example in the case of continuously observed
Mira-variables, we can test directly whether successive periods fluctuate
accidentally or not. Moreover we can also determine the probability
density function of the phase-fluctuations: psi(f). For cepheids,
eclipsing binaries and every kind of short-period variables we must get
every information for period-changes from the study of O-C diagrams.
These are for most types of periodic variables determined by the
cumulative effects of random phase fluctuations. At the Bamberg
Colloquium we have shown how the probability structure of the O-C
diagram could be determined using the central limit theorem of
probability theory (Balázs-Detre and Detre, 1965). The structure depends
on the mean square value of the phase fluctuations, sigma, where
Fig. 1. Light curves, corresponding probability density functions,
autocorrelograms and power spectra (s. text).
Lukatskaya (1966) has investigated the autocorrelation and spectral functions
of seven T Tauri-type variables and those of AE Aqr (1968), Kurochkin (1962)
those of T Orionis, and on this colloquium we shall hear Dr. Plagemann
on the same topic.
A very important question is, are the parameters of the light curves of
irregular variables constant in time, or are they changing. Tsessevitch and
Dragomineskaya (1967) investigated the light variation of 10 RW Aurigae stars
on sky patrol photographs of the Odessa, Harvard, Dushanbe and Sonneberg
observatories. They prepared probability density functions for several stars,
finding longterm variations of this function, with cycles of 25 to 60 years.
Hence, light curves of some irregular variables represent nonstationary data.
A particular random process is the so called Markov process. The property
that distinguishes Markov processes from more general random ones can be
described in non-mathematical form like this: If we know the present state of
the process, and want to make predictions about its future, then information
about the past has no predictive value, i.e. the process has no memory, its
relationship to the past does not extend beyond the immediately preceding
observation. We have a beautiful example for Markov processes in astronomy,
the O-C diagrams for periodic variables, if the period or phase fluctuations
are random, and independent from the preceding ones.
If we are able to determine the length of many individual cycles of a
variable star, as for example in the case of continuously observed
Mira-variables, we can test directly whether successive periods fluctuate
accidentally or not. Moreover we can also determine the probability
density function of the phase-fluctuations: psi(f). For cepheids,
eclipsing binaries and every kind of short-period variables we must get
every information for period-changes from the study of O-C diagrams.
These are for most types of periodic variables determined by the
cumulative effects of random phase fluctuations. At the Bamberg
Colloquium we have shown how the probability structure of the O-C
diagram could be determined using the central limit theorem of
probability theory (Balázs-Detre and Detre, 1965). The structure depends
on the mean square value of the phase fluctuations, sigma, where
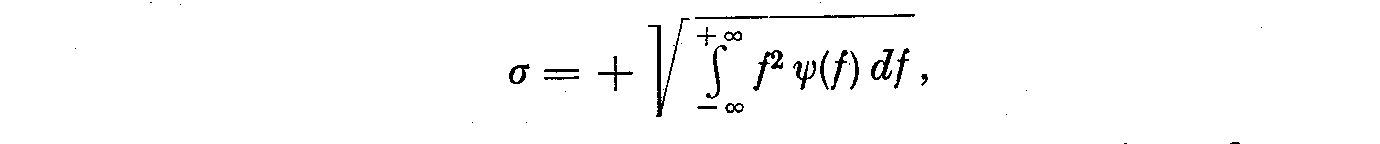 (6)
but it is highly independent from psi(f). O-C diagrams resulting from random
phase-fluctuations consist of cycles of different lengths and amplitudes.
(See Fig. 2, showing the O-C diagrams of three W Virginis-type variables:
RU Cam, AP Herculis and kappa Pavonis.)
(6)
but it is highly independent from psi(f). O-C diagrams resulting from random
phase-fluctuations consist of cycles of different lengths and amplitudes.
(See Fig. 2, showing the O-C diagrams of three W Virginis-type variables:
RU Cam, AP Herculis and kappa Pavonis.)
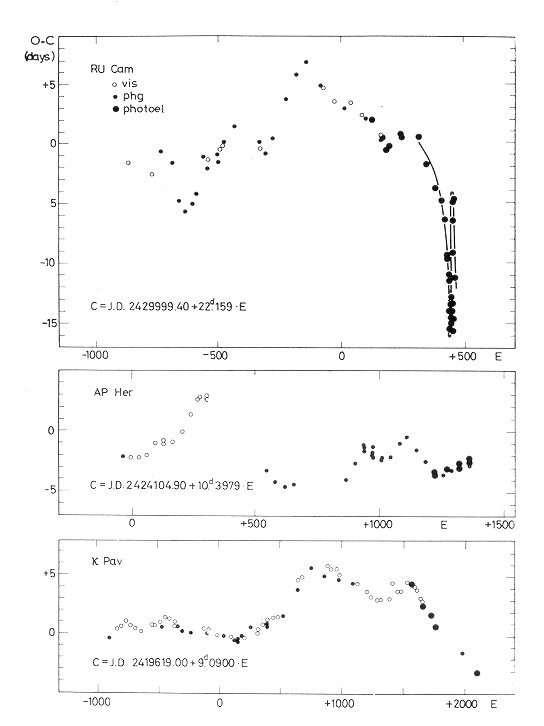 Fig. 2. O-C diagrams for three W Virginis-type variables, RU Cam,
AP Her and kappa Pav. That for AP Her is taken from Kwee (1967). For RU
Cam, the strongly oscillating phase corresponds to the recent
semiregular behaviour of the star.
Till now we have no evidence of evolutionary period-changes for most
kinds of variables. Some cyclic terms in the O-C diagrams can be interpreted
as due to binary or apsidal motion, but generally they must be treated as
cumulative effects of random fluctuations. The value of sigma can be
determined from the O-C diagrams.
Several attempts have been made to represent the time sequence of explosions
of eruptive variables by a Markov chain. Yet, as Mme Lortet-Zuckermann (1966)
has stated, the Markov chain seemed poorly adapted for the representation
of the sequence of the various sorts of explosions of the SS Cygni stars.
Stellar variability refuses compliance with simple mathematical models.
The maxima or minima of an ideally irregular variable would be distributed
at random, and the cycle lengths l would follow a Poisson-distribution:
Fig. 2. O-C diagrams for three W Virginis-type variables, RU Cam,
AP Her and kappa Pav. That for AP Her is taken from Kwee (1967). For RU
Cam, the strongly oscillating phase corresponds to the recent
semiregular behaviour of the star.
Till now we have no evidence of evolutionary period-changes for most
kinds of variables. Some cyclic terms in the O-C diagrams can be interpreted
as due to binary or apsidal motion, but generally they must be treated as
cumulative effects of random fluctuations. The value of sigma can be
determined from the O-C diagrams.
Several attempts have been made to represent the time sequence of explosions
of eruptive variables by a Markov chain. Yet, as Mme Lortet-Zuckermann (1966)
has stated, the Markov chain seemed poorly adapted for the representation
of the sequence of the various sorts of explosions of the SS Cygni stars.
Stellar variability refuses compliance with simple mathematical models.
The maxima or minima of an ideally irregular variable would be distributed
at random, and the cycle lengths l would follow a Poisson-distribution:
 (7)
Sterne (1934) has shown that the minima of R Coronae Borealis fulfill
this condition. But this conclusion is only true if the minima are
independent events, and this is certainly not the case, if the minima
are not well separated.
We see that all analyses of this kind, with the exception of the search
of hidden periodicities or changes of the statistical parameters in
time, are rather formal and do not say much about the physical nature of
the stars, since objects of the most various kinds may show similar
light curves. Combined spectroscopic and photometric, sometimes radio
observations are needed to reveal the real nature of some objects with
irregular light variation. Such combined efforts often lead to
surprising results. I mention the beautiful interpretation of V Sagittae
by Herbig, Preston, Smak and Paczynski (1965), who resolved the complex
light variations of this star into three apparently independent
activities, showing that the star is a peculiar nova-like eclipsing
binary. VV Puppis, a star formerly classified as an RR Lyrae variable,
was interpreted by Herbig (1960) likewise as a nova-like double star. In
June 1967 Deutsch (1967) has reported that the spectrum of CH Cygni,
classified earlier as a semiregular a-type variable, changed from a
normal M6 type into that of a symbiotic nova-like star. The star now
shows rapid light variations in the ultraviolet (Wallerstein 1968b).
Using new high quality spectrograms, Herbig (1966) succeeded in
interpreting the 1936 flare-up of Wachmann's star, FU Orionis, as a
phenomenon of early stellar evolution, a pre-main-sequence collapse in
conformity with Hayashi and Cameron's ideas of early stellar evolution.
Two irregular variables have recently been identified as radio sources:
BW Tauri by Penston (1968) and BL Lacertae by Schmitt (1968)*.
* BW Tau = 3C120, BL Lac = VRO 42.22.01.
These examples go to show that we need in many cases special
interpretations for individual objects. Yet, we also have some general
principles for trying the physical interpretation of broad classes of
non-periodic phenomena in variable stars. These attempts can be
classified into four categories:
1. Solar analogies. An increasing convergence is apparent between the
fields of stellar physics and solar physics, stellar analogues of solar
phenomena are becoming the subjects of specific researches. I mention a
recent interesting paper by Godoli (1967) at the Padova 1967 conference.
2. Irregular phenomena connected with or caused by the binary nature of
the star, as eruptions of different kinds or other irregularities
associated with gaseous material streaming between the components in
very short-period binaries and in symbiotic variables, further, period
variations in all kinds of eclipsing and spectroscopic binaries.
3. Irregularities connected with rotational instability of the
equatorial region of a rapidly rotating star, as in Be, Of and
Wolf-Rayet stars.
4. Veiling theories, put forward by Merrill for long-period variables*
and considered by Loreta (1934) and O'Keefe (1939) in connection with R
Coronae Borealis in terms of solid carbon particles.
* Merrill, P. W., Stellar atmospheres. The University of Chicago Press
1960. p. 512.
The closest similarity between solar activity and irregular light
variation in stars is that between solar flares and extremely sudden
increases in the integrated brightness of some stars, mainly of flare
and T Tau stars. Since Sir Lovell (1964) discovered that optical stellar
flares are accompanied by radio bursts of the I, II and III solar type,
it became very probable that flare stars show in a gigantic form the
same kind of activity as the sun. The quite irregular light curve of
T Tauri stars could be due to the superposition of very many flares,
with a variation of the activity of the star, intermingled with effects
of the neighbouring circumstellar material. We shall have introductory
papers on this theme by Wenzel and Gershberg. I refer to a recent
excellent review on flare stars by Haro (1967). Since the Prague meeting
of the IAU, Commission 27 has under Chugainov's leadership a very well
organized working group on UV Ceti type stars for cooperative radio and
optical observations.
One of the most interesting possibilities for solar analogies is the
extension of our concept of the chromosphere and of its activity to stars.
The discovery of the Wilson-Bappu (1957) effect, a correlation over a range of
nearly 16 absolute magnitudes between the widths (and not the intensity)
of the emission cores of the H and K-lines of Calcium II and the visual
absolute magnitude for stars of types G, K and M, has engendered considerable
effort to interpret this effect in terms of chromospheric macroturbulence
including all irregular, non-periodic or pseudo-periodic motions of the atoms
in a stellar atmosphere. Kraft, Preston and Wolff (1964) showed that a similar
correlation exists between the width of the hydrogen (H_alpha) absorption line
and the ultraviolet absolute magnitude. Recently Vaughan and Zirin (1968)
studied the infrared He line at lambda 10830 A which is the only line from 3000
to 11 000 A that originates solely in the chromosphere, free of changes in an
underlying photospheric line. Since the line is excited only at high temperatures,
its presence is an excellent test for hot chromospheres in late-type stars.
The sun fits the Wilson-Bappu relation, but the intensity of K_2 emission
in the integrated light of the sun is very small and can be observed with high
dispersion only. In the spectra of many stars K_2 emission is observable even
with rather small dispersion, indicating that some stars possess much more
active chromospheres than does the sun.
Leighton (1964) has shown that the K_2 emission on the sun occurs at
the edge of supergranulation cells, where photospheric magnetic fields
are sometimes found to be strengthened to the order of 100 gauss. There
is a point-to-point correlation between chromospheric activity and the
photospheric magnetic field strength. The Ca II network is not due to a
circulation of matter in the chromosphere but due to a more general
circulation which underlies the chromosphere. To the same effect points
Bonsack and Culver's (1966) result that in K-type stars the widths of
weak lines which do not have a chromospheric origin, are well correlated
with the widths of K_2 emission or the strength of the infrared He-line.
Because this emission and the strength of the infrared He-line appear
greatly enhanced in the region of solar plages and in this way it is well
correlated with the 11-year solar cycle, a study of the nature of variability
of the K_2 emission or of the He-line in other, stars should add substantially
to our understanding of both sun and stars.
That K_2 does indeed vary, has been established by Wilson and Bappu, by
Griffin (1964), Deutsch, Vaughan, and most recently by Liller (1968),
especially in the stars alpha Bootis, alpha Tauri and epsilon Geminorum. The
type of variation noted has usually been a change in the relative intensities
of the violet and red components of the K_2 emission, but there was little
evidence of periodicity analogue to the solar cycle.
Transitory Ca II emission develops at the phase of minimum radius in
cepheids and longperiod variables. The study of this phenomenon by
Herbig (1952), Jacobsen (1956) and Kraft (1957) led Kraft (1967) at the
IAU Symposium 28 to the interesting suggestion, that the behaviour of
cepheids at this phase is an exaggeration of the disturbed sun. At the
time of minimum radius the surface of the cepheids becomes covered with
something like plages. As the cycle progresses, a shock wave moves
through the atmosphere and all such solar-like disturbances disappear:
the cepheid becomes an F-type star.
Some non-periodic secondary variations in eclipsing binaries were
attributed to star spots (Kron, 1947, 1952). But these stars are not
adapted for such investigations, because gas streams between and around
the components may cause irregularities in the light curve.
Prominence activity was found in supergiant stars, for example in 31
Cygni, which are components of eclipsing systems. When the star goes
behind the atmosphere of the supergiant K3 star, at times several
absorption components due to Calcium II H and K are seen, providing
unmistakable evidence that bodies of gas moving with discrete velocities
exist in its atmosphere (S. Underhill, 1960).
Mass loss in stars might bear a relation to the solar wind, which is a
plasma extension of the solar corona moving outward at the velocity of
about 500 km/sec carrying away a mass of about 10^-13 solar mass per year
and the frozen-in magnetic fields from the sun. The solar wind has a
steady continuous and an irregularly varying component. The evidence
that considerable mass loss occurs in stars apart from novae,
supernovae and close binaries, came from Deutsch's (1956) remarkable
discovery of a set of circumstellar lines in the visual companion of the
M supergiant alpha Herculis. There is now ample spectroscopic evidence for
the efflux of cool gas from the surfaces of all giant stars
with spectral types later than M0 (Deutsch, 1966), at a rate of some
10^-9 solar mass per year. Weyman (1962) pointed out the difficulties in
the way of a solar wind explanation for these phenomena. More violent
mass losses from stars are certainly not of the solar wind type. In some
pulsating stars the pulsation shock can be so violent that the surface
layer may be driven away from the star in a relatively small number of
periods, as was shown by Christy (1965) for W Virginis stars. According
to Paczynski and Ziólkowski (1968) Mira type variables may throw out
their envelopes and in this way planetary nebulae might be formed. Mass
loss may be the dominating factor in horizontal branch evolution rather
than nuclear burning. Kuhi (1964, 1966) estimated the rate of mass loss
from T Tauri stars at about 10^-7 solar mass per year. Spectra secured
from rocket flights provided first evidence for the extremely violent
ejection processes in the atmospheres of O and B-type supergiants and
bright giants (Jenkins and Morton, 1967). We shall hear more on this
subject next week in Trieste, where a Colloquium will be held on mass
loss from stars.
The weak point of solar analogies is that solar phenomena are not yet
quite understood. Yet, we can be certain of the magnetic nature of all
processes of solar activity and that all its accompanying phenomena like
spots, faculae, flares, the irregular component of solar wind, etc. are
connected with local concentration as well as annihilation of magnetic
fields. Hence it is very probable that also the analogous stellar
phenomena are of magnetic origin.
Moreover, it becomes increasingly evident that magnetic fields may have
a share also in other aspects of stellar irregularities. E.g., Merrill's
veiling theory is supported by Serkowski's (1966a, b) recent discovery
of large amounts of plane polarization in some Mira stars at minimum
light. This polarization can be explained by graphite flakes, condensed
in the atmosphere of these stars, presuming that they are aligned by
stellar magnetic fields (Donn et al. 1966; Wickramasinghe 1968).
Magnetic forces may play an important role in the formation of the
envelopes of Be stars. Of course, Struve's (1931) suggestion of
rotationally forced ejection in a star rotating at the rotational limit
in which its equatorial rotational velocity is first sufficient to
balance by centrifugal effects the gravitational attraction of the star
at its equator, is correct. But an additional force is required to move
the matter outward from the region just above the star's equator. The
complex kinematic behaviour of the shell, the occurrence of stars such
as Pleione, which seem able to lose and reform their shell at intervals,
is particularly suggestive of the presence of forces which trend to
drive the gases away from the star. Even quite weak magnetic fields
could produce significant dynamical effects in such a shell (Crampin and
Hoyle 1960; Limber and Marlborough 1968). Hazlehurst (1967) studied in a
recent paper the magnetic release of a circumstellar ring, and he found
that the gases describe a decelerated motion, compatible with the
observed spectral properties of circumstellar shells. From the ultimate
velocity of the material an observational determination of the magnetic
field in the stellar photosphere will be possible.*
* About problems of irregular variations in light and radial velocity of
Be, Of and WR stars I refer to the excellent book The Early Type Stars
by Anne B. Underhill (Reidel Publishing Company, 1966).
We would have a better understanding of the observed period-variations
in eclipsing binaries, if an adequate electromagnetic theory of the gaseous
streams in the systems had been elaborated. It appears from the work by
Plavec and Schneller that the most erratic O-C diagrams are obtained for
contact and undetached systems. If an O-C diagram has random walk
properties, then the underlying physical processes that give rise to
the random period fluctuations, are themselves random processes. Wood's
hypothesis of mass ejection for the explanation of the period
fluctuations, if the areas of ejection are distributed over the surface
at random, fits the criterion of randomness, but the required masses are
too high. However, we might have a very efficient agent for angular
momentum changes in the interaction of the ionized gaseous streams
moving around the components with the magnetic fields of the stars.
Magnetic fields might play an even greater role in hot short-period
eruptive binaries and in symbiotic stars. Babcock measured a magnetic field
of 1000 gauss in the symbiotic variable AG Pegasi. The configuration in
eruptive binaries, a highly ionized disk, a strongly flickering hot component
ejecting highly ionized material into the disk, might be extremely unstable,
especially if the components have strong magnetic fields. It is just possible
that the magnetic and gravitational instability of such a configuration might
lead from time to time to major eruptions. According to my opinion the seat of
the eruptions might be the plasma surrounding the stars, not a stellar
component.
According to Ambarzumjan's (1954) hypothesis, the continuous emission
observed in the spectra of the T Tauri type variables and UV Ceti type
stars during their outbursts originates from relativistic electrons in
the magnetic fields of these stars.
Random processes may influence the pulsation of the stars, giving rise
to irregular fluctuations in the light and radial velocity curve and in
the period. The triggering mechanism of the pulsation, which is sought
in the convective layers of the stars, may especially be sensitive to
magnetic activity.
Epstein (1950) has shown in an important paper that in highly centrally
concentrated stellar models the period of the fundamental mode is
determined primarily by conditions in the envelope and that the period
is almost independent of conditions in the central regions where most of
the mass is located. This result suggests that stellar pulsation, at
least in giant and supergiant-like stars, is a fairly superficial
phenomenon effecting only the outer stellar layers. The higher modes are
even more sensitive to properties of the most external layers of the
star, since these modes have higher relative amplitudes near the
surface.
Indeed, red variables, where the outer layers play a great role, have
very erratic light variation, whereas classical Cepheids and most RR
Lyrae stars show very little if any irregularities.
Zhevakin introduced the peripheral zone of He II critical ionization
as the excitation mechanism of the pulsation. He (1959) developed an
interesting theory of semiregular and irregular variables. The period of
oscillation of the inner region of the star is constant to a high degree
of accuracy. The nonadiabatic oscillations of the atmosphere show
relative to the adiabatic oscillations of the inner regions a phase
shift, whose value depends primarily on how close is the ionization zone
to the stellar surface. Random fluctuations in the position of the zone
change the phase shift, and in this way the period of the outer zones
will fluctuate about the period of oscillations of the inner region.
If the driving mechanism of the pulsation is affected by random
perturbations, wee may expect a suppression of the amplitude of the
pulsation relative to stars free from such perturbations. As it is well
known, semiregular red variables differ from the longperiod variables
only in their smaller amplitudes (Fig. 3).
The RR Lyrae-variables with the Blashko-effect have very complicated
O-C diagrams. Though the Blashko-effect is a periodic phenomenon, it
causes great random fluctuations both in the fundamental and in the
secondary period (Fig. 4). As a period-amplitude diagram for RRab-stars
in M3, taken from a paper by Szeidl (1965), shows (Fig. 5), the mean
amplitudes of the RRab stars with Blashko-effect are much smaller than
the amplitudes of RRab stars with stable light curves.
Babcock discovered a strongly variable, magnetic field in RR Lyrae
which ranges from +1200 to -1600 gauss. Julia Balázs (1959) has shown
that there was some correlation between Babcock's measures and the
Blashko-effect of this star: the maximum positive and maximum negative
fields were associated with the maximum and minimum light amplitudes,
respectively.
(7)
Sterne (1934) has shown that the minima of R Coronae Borealis fulfill
this condition. But this conclusion is only true if the minima are
independent events, and this is certainly not the case, if the minima
are not well separated.
We see that all analyses of this kind, with the exception of the search
of hidden periodicities or changes of the statistical parameters in
time, are rather formal and do not say much about the physical nature of
the stars, since objects of the most various kinds may show similar
light curves. Combined spectroscopic and photometric, sometimes radio
observations are needed to reveal the real nature of some objects with
irregular light variation. Such combined efforts often lead to
surprising results. I mention the beautiful interpretation of V Sagittae
by Herbig, Preston, Smak and Paczynski (1965), who resolved the complex
light variations of this star into three apparently independent
activities, showing that the star is a peculiar nova-like eclipsing
binary. VV Puppis, a star formerly classified as an RR Lyrae variable,
was interpreted by Herbig (1960) likewise as a nova-like double star. In
June 1967 Deutsch (1967) has reported that the spectrum of CH Cygni,
classified earlier as a semiregular a-type variable, changed from a
normal M6 type into that of a symbiotic nova-like star. The star now
shows rapid light variations in the ultraviolet (Wallerstein 1968b).
Using new high quality spectrograms, Herbig (1966) succeeded in
interpreting the 1936 flare-up of Wachmann's star, FU Orionis, as a
phenomenon of early stellar evolution, a pre-main-sequence collapse in
conformity with Hayashi and Cameron's ideas of early stellar evolution.
Two irregular variables have recently been identified as radio sources:
BW Tauri by Penston (1968) and BL Lacertae by Schmitt (1968)*.
* BW Tau = 3C120, BL Lac = VRO 42.22.01.
These examples go to show that we need in many cases special
interpretations for individual objects. Yet, we also have some general
principles for trying the physical interpretation of broad classes of
non-periodic phenomena in variable stars. These attempts can be
classified into four categories:
1. Solar analogies. An increasing convergence is apparent between the
fields of stellar physics and solar physics, stellar analogues of solar
phenomena are becoming the subjects of specific researches. I mention a
recent interesting paper by Godoli (1967) at the Padova 1967 conference.
2. Irregular phenomena connected with or caused by the binary nature of
the star, as eruptions of different kinds or other irregularities
associated with gaseous material streaming between the components in
very short-period binaries and in symbiotic variables, further, period
variations in all kinds of eclipsing and spectroscopic binaries.
3. Irregularities connected with rotational instability of the
equatorial region of a rapidly rotating star, as in Be, Of and
Wolf-Rayet stars.
4. Veiling theories, put forward by Merrill for long-period variables*
and considered by Loreta (1934) and O'Keefe (1939) in connection with R
Coronae Borealis in terms of solid carbon particles.
* Merrill, P. W., Stellar atmospheres. The University of Chicago Press
1960. p. 512.
The closest similarity between solar activity and irregular light
variation in stars is that between solar flares and extremely sudden
increases in the integrated brightness of some stars, mainly of flare
and T Tau stars. Since Sir Lovell (1964) discovered that optical stellar
flares are accompanied by radio bursts of the I, II and III solar type,
it became very probable that flare stars show in a gigantic form the
same kind of activity as the sun. The quite irregular light curve of
T Tauri stars could be due to the superposition of very many flares,
with a variation of the activity of the star, intermingled with effects
of the neighbouring circumstellar material. We shall have introductory
papers on this theme by Wenzel and Gershberg. I refer to a recent
excellent review on flare stars by Haro (1967). Since the Prague meeting
of the IAU, Commission 27 has under Chugainov's leadership a very well
organized working group on UV Ceti type stars for cooperative radio and
optical observations.
One of the most interesting possibilities for solar analogies is the
extension of our concept of the chromosphere and of its activity to stars.
The discovery of the Wilson-Bappu (1957) effect, a correlation over a range of
nearly 16 absolute magnitudes between the widths (and not the intensity)
of the emission cores of the H and K-lines of Calcium II and the visual
absolute magnitude for stars of types G, K and M, has engendered considerable
effort to interpret this effect in terms of chromospheric macroturbulence
including all irregular, non-periodic or pseudo-periodic motions of the atoms
in a stellar atmosphere. Kraft, Preston and Wolff (1964) showed that a similar
correlation exists between the width of the hydrogen (H_alpha) absorption line
and the ultraviolet absolute magnitude. Recently Vaughan and Zirin (1968)
studied the infrared He line at lambda 10830 A which is the only line from 3000
to 11 000 A that originates solely in the chromosphere, free of changes in an
underlying photospheric line. Since the line is excited only at high temperatures,
its presence is an excellent test for hot chromospheres in late-type stars.
The sun fits the Wilson-Bappu relation, but the intensity of K_2 emission
in the integrated light of the sun is very small and can be observed with high
dispersion only. In the spectra of many stars K_2 emission is observable even
with rather small dispersion, indicating that some stars possess much more
active chromospheres than does the sun.
Leighton (1964) has shown that the K_2 emission on the sun occurs at
the edge of supergranulation cells, where photospheric magnetic fields
are sometimes found to be strengthened to the order of 100 gauss. There
is a point-to-point correlation between chromospheric activity and the
photospheric magnetic field strength. The Ca II network is not due to a
circulation of matter in the chromosphere but due to a more general
circulation which underlies the chromosphere. To the same effect points
Bonsack and Culver's (1966) result that in K-type stars the widths of
weak lines which do not have a chromospheric origin, are well correlated
with the widths of K_2 emission or the strength of the infrared He-line.
Because this emission and the strength of the infrared He-line appear
greatly enhanced in the region of solar plages and in this way it is well
correlated with the 11-year solar cycle, a study of the nature of variability
of the K_2 emission or of the He-line in other, stars should add substantially
to our understanding of both sun and stars.
That K_2 does indeed vary, has been established by Wilson and Bappu, by
Griffin (1964), Deutsch, Vaughan, and most recently by Liller (1968),
especially in the stars alpha Bootis, alpha Tauri and epsilon Geminorum. The
type of variation noted has usually been a change in the relative intensities
of the violet and red components of the K_2 emission, but there was little
evidence of periodicity analogue to the solar cycle.
Transitory Ca II emission develops at the phase of minimum radius in
cepheids and longperiod variables. The study of this phenomenon by
Herbig (1952), Jacobsen (1956) and Kraft (1957) led Kraft (1967) at the
IAU Symposium 28 to the interesting suggestion, that the behaviour of
cepheids at this phase is an exaggeration of the disturbed sun. At the
time of minimum radius the surface of the cepheids becomes covered with
something like plages. As the cycle progresses, a shock wave moves
through the atmosphere and all such solar-like disturbances disappear:
the cepheid becomes an F-type star.
Some non-periodic secondary variations in eclipsing binaries were
attributed to star spots (Kron, 1947, 1952). But these stars are not
adapted for such investigations, because gas streams between and around
the components may cause irregularities in the light curve.
Prominence activity was found in supergiant stars, for example in 31
Cygni, which are components of eclipsing systems. When the star goes
behind the atmosphere of the supergiant K3 star, at times several
absorption components due to Calcium II H and K are seen, providing
unmistakable evidence that bodies of gas moving with discrete velocities
exist in its atmosphere (S. Underhill, 1960).
Mass loss in stars might bear a relation to the solar wind, which is a
plasma extension of the solar corona moving outward at the velocity of
about 500 km/sec carrying away a mass of about 10^-13 solar mass per year
and the frozen-in magnetic fields from the sun. The solar wind has a
steady continuous and an irregularly varying component. The evidence
that considerable mass loss occurs in stars apart from novae,
supernovae and close binaries, came from Deutsch's (1956) remarkable
discovery of a set of circumstellar lines in the visual companion of the
M supergiant alpha Herculis. There is now ample spectroscopic evidence for
the efflux of cool gas from the surfaces of all giant stars
with spectral types later than M0 (Deutsch, 1966), at a rate of some
10^-9 solar mass per year. Weyman (1962) pointed out the difficulties in
the way of a solar wind explanation for these phenomena. More violent
mass losses from stars are certainly not of the solar wind type. In some
pulsating stars the pulsation shock can be so violent that the surface
layer may be driven away from the star in a relatively small number of
periods, as was shown by Christy (1965) for W Virginis stars. According
to Paczynski and Ziólkowski (1968) Mira type variables may throw out
their envelopes and in this way planetary nebulae might be formed. Mass
loss may be the dominating factor in horizontal branch evolution rather
than nuclear burning. Kuhi (1964, 1966) estimated the rate of mass loss
from T Tauri stars at about 10^-7 solar mass per year. Spectra secured
from rocket flights provided first evidence for the extremely violent
ejection processes in the atmospheres of O and B-type supergiants and
bright giants (Jenkins and Morton, 1967). We shall hear more on this
subject next week in Trieste, where a Colloquium will be held on mass
loss from stars.
The weak point of solar analogies is that solar phenomena are not yet
quite understood. Yet, we can be certain of the magnetic nature of all
processes of solar activity and that all its accompanying phenomena like
spots, faculae, flares, the irregular component of solar wind, etc. are
connected with local concentration as well as annihilation of magnetic
fields. Hence it is very probable that also the analogous stellar
phenomena are of magnetic origin.
Moreover, it becomes increasingly evident that magnetic fields may have
a share also in other aspects of stellar irregularities. E.g., Merrill's
veiling theory is supported by Serkowski's (1966a, b) recent discovery
of large amounts of plane polarization in some Mira stars at minimum
light. This polarization can be explained by graphite flakes, condensed
in the atmosphere of these stars, presuming that they are aligned by
stellar magnetic fields (Donn et al. 1966; Wickramasinghe 1968).
Magnetic forces may play an important role in the formation of the
envelopes of Be stars. Of course, Struve's (1931) suggestion of
rotationally forced ejection in a star rotating at the rotational limit
in which its equatorial rotational velocity is first sufficient to
balance by centrifugal effects the gravitational attraction of the star
at its equator, is correct. But an additional force is required to move
the matter outward from the region just above the star's equator. The
complex kinematic behaviour of the shell, the occurrence of stars such
as Pleione, which seem able to lose and reform their shell at intervals,
is particularly suggestive of the presence of forces which trend to
drive the gases away from the star. Even quite weak magnetic fields
could produce significant dynamical effects in such a shell (Crampin and
Hoyle 1960; Limber and Marlborough 1968). Hazlehurst (1967) studied in a
recent paper the magnetic release of a circumstellar ring, and he found
that the gases describe a decelerated motion, compatible with the
observed spectral properties of circumstellar shells. From the ultimate
velocity of the material an observational determination of the magnetic
field in the stellar photosphere will be possible.*
* About problems of irregular variations in light and radial velocity of
Be, Of and WR stars I refer to the excellent book The Early Type Stars
by Anne B. Underhill (Reidel Publishing Company, 1966).
We would have a better understanding of the observed period-variations
in eclipsing binaries, if an adequate electromagnetic theory of the gaseous
streams in the systems had been elaborated. It appears from the work by
Plavec and Schneller that the most erratic O-C diagrams are obtained for
contact and undetached systems. If an O-C diagram has random walk
properties, then the underlying physical processes that give rise to
the random period fluctuations, are themselves random processes. Wood's
hypothesis of mass ejection for the explanation of the period
fluctuations, if the areas of ejection are distributed over the surface
at random, fits the criterion of randomness, but the required masses are
too high. However, we might have a very efficient agent for angular
momentum changes in the interaction of the ionized gaseous streams
moving around the components with the magnetic fields of the stars.
Magnetic fields might play an even greater role in hot short-period
eruptive binaries and in symbiotic stars. Babcock measured a magnetic field
of 1000 gauss in the symbiotic variable AG Pegasi. The configuration in
eruptive binaries, a highly ionized disk, a strongly flickering hot component
ejecting highly ionized material into the disk, might be extremely unstable,
especially if the components have strong magnetic fields. It is just possible
that the magnetic and gravitational instability of such a configuration might
lead from time to time to major eruptions. According to my opinion the seat of
the eruptions might be the plasma surrounding the stars, not a stellar
component.
According to Ambarzumjan's (1954) hypothesis, the continuous emission
observed in the spectra of the T Tauri type variables and UV Ceti type
stars during their outbursts originates from relativistic electrons in
the magnetic fields of these stars.
Random processes may influence the pulsation of the stars, giving rise
to irregular fluctuations in the light and radial velocity curve and in
the period. The triggering mechanism of the pulsation, which is sought
in the convective layers of the stars, may especially be sensitive to
magnetic activity.
Epstein (1950) has shown in an important paper that in highly centrally
concentrated stellar models the period of the fundamental mode is
determined primarily by conditions in the envelope and that the period
is almost independent of conditions in the central regions where most of
the mass is located. This result suggests that stellar pulsation, at
least in giant and supergiant-like stars, is a fairly superficial
phenomenon effecting only the outer stellar layers. The higher modes are
even more sensitive to properties of the most external layers of the
star, since these modes have higher relative amplitudes near the
surface.
Indeed, red variables, where the outer layers play a great role, have
very erratic light variation, whereas classical Cepheids and most RR
Lyrae stars show very little if any irregularities.
Zhevakin introduced the peripheral zone of He II critical ionization
as the excitation mechanism of the pulsation. He (1959) developed an
interesting theory of semiregular and irregular variables. The period of
oscillation of the inner region of the star is constant to a high degree
of accuracy. The nonadiabatic oscillations of the atmosphere show
relative to the adiabatic oscillations of the inner regions a phase
shift, whose value depends primarily on how close is the ionization zone
to the stellar surface. Random fluctuations in the position of the zone
change the phase shift, and in this way the period of the outer zones
will fluctuate about the period of oscillations of the inner region.
If the driving mechanism of the pulsation is affected by random
perturbations, wee may expect a suppression of the amplitude of the
pulsation relative to stars free from such perturbations. As it is well
known, semiregular red variables differ from the longperiod variables
only in their smaller amplitudes (Fig. 3).
The RR Lyrae-variables with the Blashko-effect have very complicated
O-C diagrams. Though the Blashko-effect is a periodic phenomenon, it
causes great random fluctuations both in the fundamental and in the
secondary period (Fig. 4). As a period-amplitude diagram for RRab-stars
in M3, taken from a paper by Szeidl (1965), shows (Fig. 5), the mean
amplitudes of the RRab stars with Blashko-effect are much smaller than
the amplitudes of RRab stars with stable light curves.
Babcock discovered a strongly variable, magnetic field in RR Lyrae
which ranges from +1200 to -1600 gauss. Julia Balázs (1959) has shown
that there was some correlation between Babcock's measures and the
Blashko-effect of this star: the maximum positive and maximum negative
fields were associated with the maximum and minimum light amplitudes,
respectively.
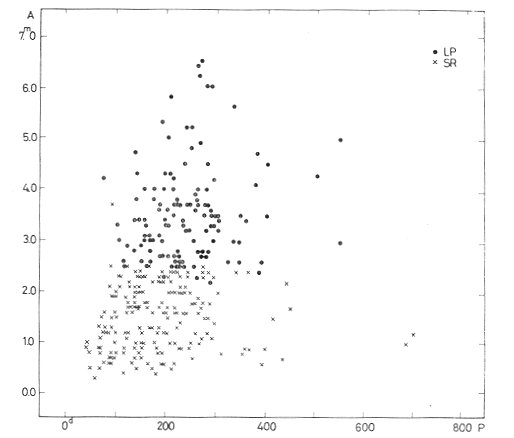 Fig. 3. Period-amplitude relation for longperiod (points) and semiregular
(crosses) variables in Sagittarius.
Fig. 3. Period-amplitude relation for longperiod (points) and semiregular
(crosses) variables in Sagittarius.
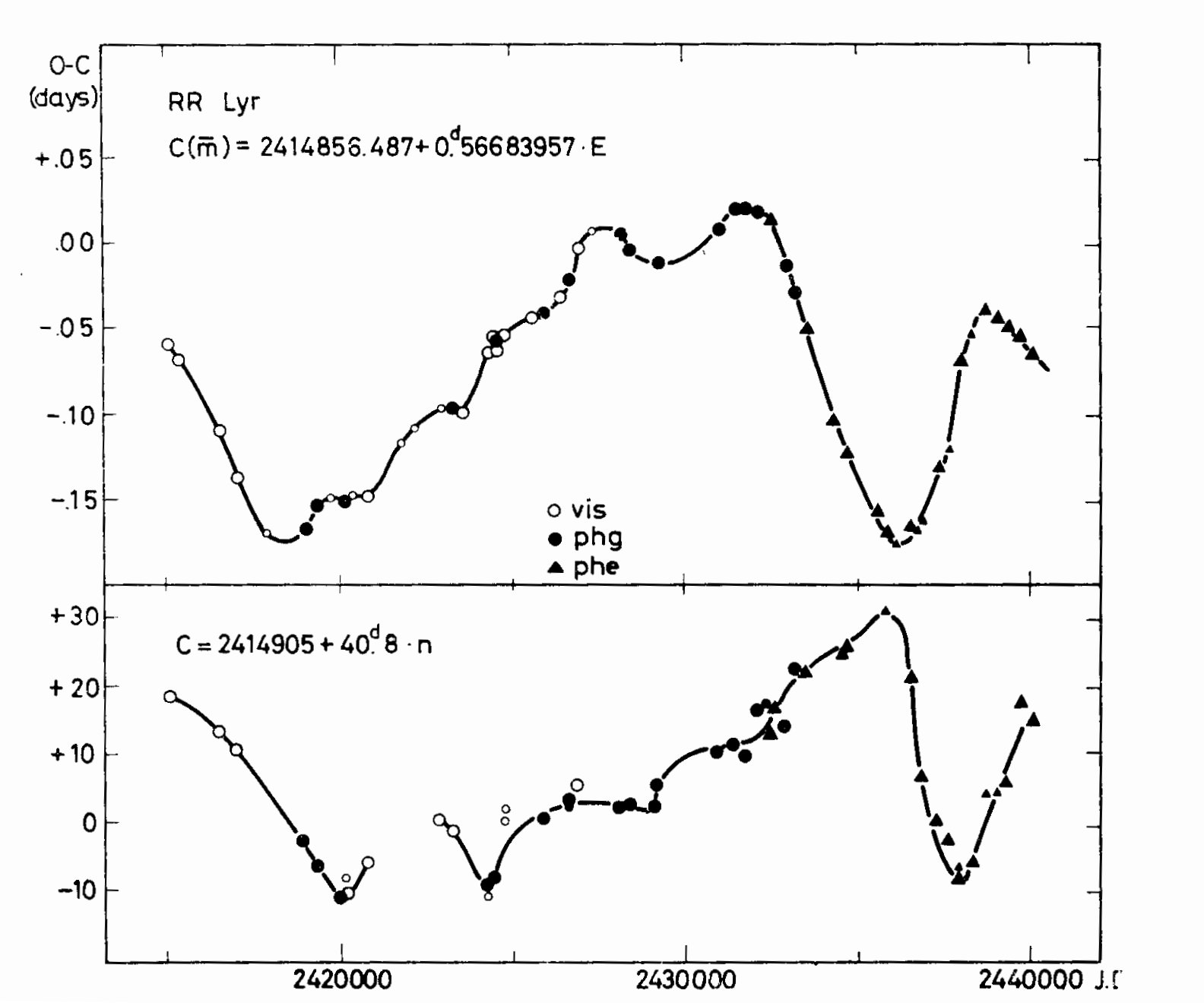 Fig. 4. O-C diagrams for the fundamental and secondary periods of RR Lyrae.
She made the proposal that RR Lyrae is an oblique rotator with a
rotation period of 41 days, which is the period of the Blashko-effect.
Preston (1967) has observed RR Lyrae for the Zeeman effect in 1963 and
1964 some 50 times and has not once found a measurable field. Yet, this
negative result does not disprove, that the Blashko-effect and the
irregularities connected with it are of magnetic origin. As Fig. 6
prepared by Szeidl shows, the Blashko-effect is a very erratic
phenomenon, the amplitude of the phase variations and that of the
maximum light variations are changing strongly from time to time, they
are sometimes scarcely observable.* The same may happen with the
magnetic field. In any case, the greatest part of magnetic activity
might take place, as on the sun, below the photosphere.
* In RR Gem a strong Blashko-effect was observed till about 1937 which
disappeared later.
For Delta Scuti variables and dwarf Cepheids we do not observe the
suppression of the amplitude in stars with secondary periodicities,
and such stars have the same simple O-C diagrams as variables with
stable light curves. Here, the secondary periods may originate from non
random influences, e.g. from tidal effects as proposed by Fitch (1962).
Fig. 4. O-C diagrams for the fundamental and secondary periods of RR Lyrae.
She made the proposal that RR Lyrae is an oblique rotator with a
rotation period of 41 days, which is the period of the Blashko-effect.
Preston (1967) has observed RR Lyrae for the Zeeman effect in 1963 and
1964 some 50 times and has not once found a measurable field. Yet, this
negative result does not disprove, that the Blashko-effect and the
irregularities connected with it are of magnetic origin. As Fig. 6
prepared by Szeidl shows, the Blashko-effect is a very erratic
phenomenon, the amplitude of the phase variations and that of the
maximum light variations are changing strongly from time to time, they
are sometimes scarcely observable.* The same may happen with the
magnetic field. In any case, the greatest part of magnetic activity
might take place, as on the sun, below the photosphere.
* In RR Gem a strong Blashko-effect was observed till about 1937 which
disappeared later.
For Delta Scuti variables and dwarf Cepheids we do not observe the
suppression of the amplitude in stars with secondary periodicities,
and such stars have the same simple O-C diagrams as variables with
stable light curves. Here, the secondary periods may originate from non
random influences, e.g. from tidal effects as proposed by Fitch (1962).
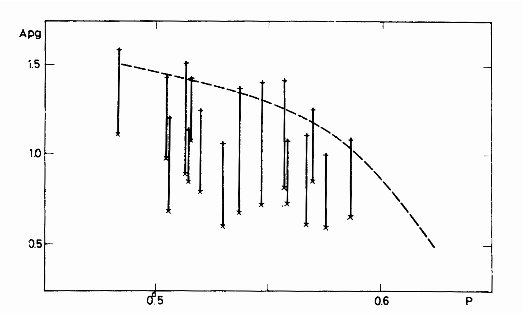 Fig. 5. Period-amplitude diagram for RRab stars in M3 according to Szeidl (1965)
The dotted line shows the relation valid for stable light curves, the vertical
lines show the limits of A_pg for RRab stars with Blashko-effect.
RU Camelopardalis, a peculiar W Virginis-type Cepheid offers now a
unique opportunity for studying the interplay between pulsation and
irregular stellar activity. Demers and Fernie (1966) made three years
ago the remarkable discovery that the star nearly stopped its light
variation. Considering all available photoelectric observations I was
able to show (Detre 1966) that the star exhibited cyclic amplitude
variations with a mean cycle of about 5 years. Therefore, I expected an
increase in the amplitude for the year 1967. Indeed the amplitude began
to increase in the spring 1967, and in the summer it reached 0.3 mg. in
V and nearly half a magnitude in B. But immediately, after Fernie and
myself have reported about this amplitude increase at the Prague IAU
meeting, the amplitude came back very rapidly to the small value it had
in 1966 (Fig. 7). At first the light minimum, a little later the maximum
passed to its former value. The star needed in both cases only four
cycles of its 22 day-variation to restore the small amplitude.
The most important point we should know, how the spectrum changed.
Faraggiana and Hack (1967) studied 11 high dispersion spectrograms taken
by Prof. Deutsch between 1956 and 1961 when the light amplitude was
normal. They observed hydrogen emission-lines from minimum to maximum
and emission cores in the H and K lines on all the spectrograms
sufficiently exposed in this region. The radial velocity curve obtained
from these lines was shifted with respect to the curve for the
absorption lines by about -70 km/sec, suggesting that the chromosphere
of the star was in expansion. Demers and Crampton (1966) taking spectra
during the small amplitude stage, state that no emission lines are
visible. To the same conclusion comes Wallerstein (1967, 1968) using
Lick coudé spectra. But unfortunately, these spectra do not contain the H,
K lines region. I wonder if there are any spectra taken during the
quiescent or temporary recovery stage similar to those obtained formerly
by Prof. Deutsch.
According to my opinion the pulsation mechanism of the star is very sensitive
to changes of its magnetic field and we witness the effects of such changes in
the last time. I hope, the star will yet give opportunity to study this
question. At present it shows irregular light variations with a V-amplitude
smaller than 0.1 magnitude.
Fig. 5. Period-amplitude diagram for RRab stars in M3 according to Szeidl (1965)
The dotted line shows the relation valid for stable light curves, the vertical
lines show the limits of A_pg for RRab stars with Blashko-effect.
RU Camelopardalis, a peculiar W Virginis-type Cepheid offers now a
unique opportunity for studying the interplay between pulsation and
irregular stellar activity. Demers and Fernie (1966) made three years
ago the remarkable discovery that the star nearly stopped its light
variation. Considering all available photoelectric observations I was
able to show (Detre 1966) that the star exhibited cyclic amplitude
variations with a mean cycle of about 5 years. Therefore, I expected an
increase in the amplitude for the year 1967. Indeed the amplitude began
to increase in the spring 1967, and in the summer it reached 0.3 mg. in
V and nearly half a magnitude in B. But immediately, after Fernie and
myself have reported about this amplitude increase at the Prague IAU
meeting, the amplitude came back very rapidly to the small value it had
in 1966 (Fig. 7). At first the light minimum, a little later the maximum
passed to its former value. The star needed in both cases only four
cycles of its 22 day-variation to restore the small amplitude.
The most important point we should know, how the spectrum changed.
Faraggiana and Hack (1967) studied 11 high dispersion spectrograms taken
by Prof. Deutsch between 1956 and 1961 when the light amplitude was
normal. They observed hydrogen emission-lines from minimum to maximum
and emission cores in the H and K lines on all the spectrograms
sufficiently exposed in this region. The radial velocity curve obtained
from these lines was shifted with respect to the curve for the
absorption lines by about -70 km/sec, suggesting that the chromosphere
of the star was in expansion. Demers and Crampton (1966) taking spectra
during the small amplitude stage, state that no emission lines are
visible. To the same conclusion comes Wallerstein (1967, 1968) using
Lick coudé spectra. But unfortunately, these spectra do not contain the H,
K lines region. I wonder if there are any spectra taken during the
quiescent or temporary recovery stage similar to those obtained formerly
by Prof. Deutsch.
According to my opinion the pulsation mechanism of the star is very sensitive
to changes of its magnetic field and we witness the effects of such changes in
the last time. I hope, the star will yet give opportunity to study this
question. At present it shows irregular light variations with a V-amplitude
smaller than 0.1 magnitude.
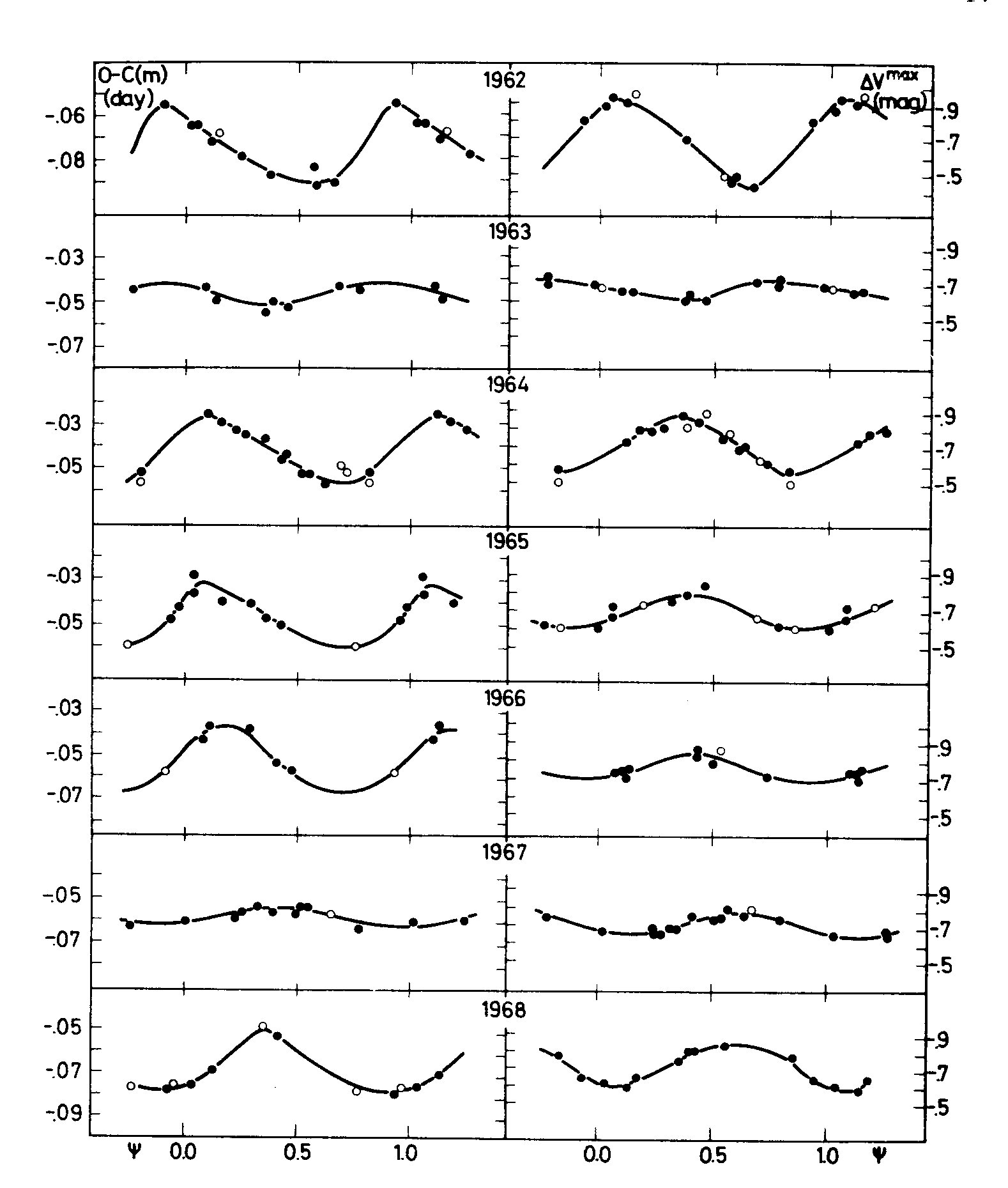 Fig. 6. Variations in the Blashko-effect of RR Lyrae.
Fig. 6. Variations in the Blashko-effect of RR Lyrae.
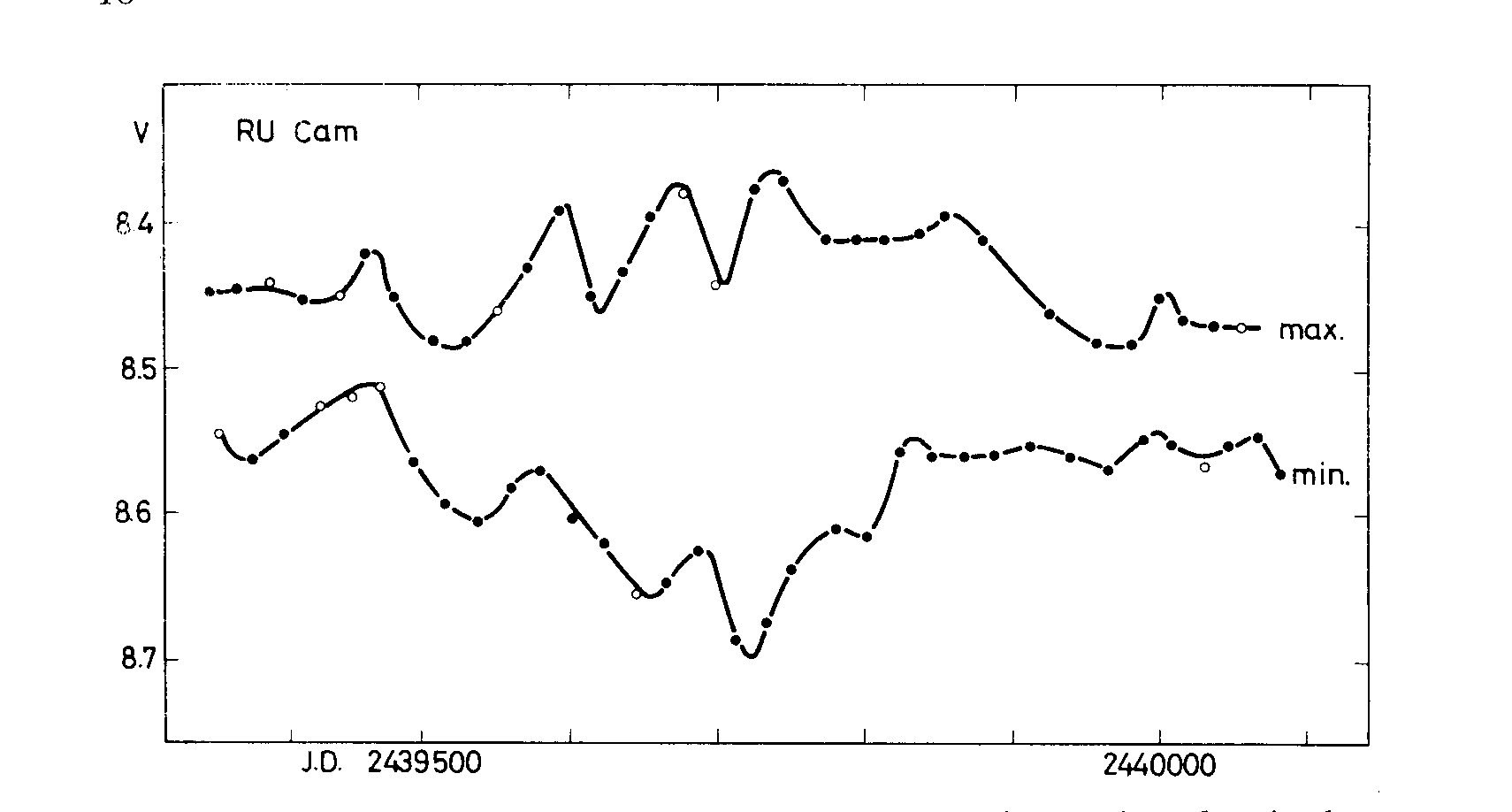 Fig. 7. Light maxima and minima of RU Cam in V, according to photoelectric
observations obtained by Szeidl at the 24" reflector of the Konkoly Observatory.
I have only touched some few aspects of irregular stellar activity. Our
field is tremendous. From the theoretical side it comprises questions of
stellar stability, pulsation theory, turbulence and shock wave theory,
i.e., the dynamic theory of stellar envelopes, further, celestial
mechanics, magnetohydrodynamics and questions of stellar evolution. From
the observational side it extends over all periodic or non-periodic
variables, over intrinsic as well as eclipsing variables. Its complete
understanding postulates the knowledge of solar physics in highest
degree. And the reason for not yet proposing a symposium with solar
physicists, is because they would have a great advantage over us. We may
hope that not in the far future variable star astronomers will be able
to give the same help to solar physicists as they give at present to us.
REFERENCES
Ambarzumjan, V. A., 1954. Comm. Byurakan Obs. No. 13.
Ashbrook, J., Duncombe, R. L. and Van Woerkom, A. J. J., 1954, Astr. J. 59, 12.
Balázs-Detre, Julia and Detre, L., 1965, Kl. Veröff. Remeis-Sternw. Bamberg IV,
No. 40 p. 184.
Balázs-Detre, Julia, 1959, Kl. Veröff. Remeis-Sternw. Bamberg 27, 26.
Bonsack W. K. and Culver, R. B., 1966, Astrophys. J. 145, 767.
Christy, R. F., 1965, Kl. Veröff. Remeis-Sternw. Bamberg, 40, 77.
Crampin, J. and Hoyle, F., 1960, Mon. Not. R. astr. Soc. 120, 33.
Demers, S. and Crampton, D., 1966, Astr. J. 71, 852.
Demers, S. and Fernie, J. D., 1966, Astrophys. J. 144, 440.
Detre, L., 1966, Inf. Bul. Var. Stars No. 152. (IBVS N°.152)
Deutsch, A. J., 1956, Astrophys. J. 123, 210.
Deutsch, A. J., 1966, Stellar Evolution. Plenum Press New York p. 377.
Deutsch, A. J., 1967, IAU Circ. No. 2020.
Donn, B., Stecher, T. P., Wickramasinghe, N. C. and Williams, D. A., 1966, Astrophys.
J. 145, 949.
Durney, B. R., Faulkner, J., Gribbin, J. R. and Roxburgh, I. W., 1968, Nature 218, 20.
Epstein, J., 1950, Astrophys. J. 112, 6.
Faraggiana, R. and Hack, M., 1967, Z. Astrophys. 66, 343.
Godoli, G., 1967, Atti dell'XI. Convegno, Padova, p. 224.
Griffin, R. F., 1964, Observatory 83, 255.
Haro, G., 1967, Stars and Stellar Systems. Vol. VIII. 141.
Hazlehurst, J., 1967, Z. Astrophys. 65, 311.
Herbig, G. H., 1952, Astrophys. J. 116, 369.
Herbig, G. H., 1960, Astrophys. J. 132, 76.
Herbig, G. H., 1966, Vistas in Astr. 8, 109.
Herbig, G. H., Preston, G. W., Smak, J. and Paczynski, B., 1967, Astrophys. J. 141, 617.
Herbig, G. H., 1968. Inf. Bul. Var. Stars No. 243. (IBVS N°.243)
Jacobsen, T. S., 1960, Publ. Dom. Astrophys. Obs. Victoria 10, 145.
Jenkins, E. B. and Morton, D. C., 1967, Nature 215, 1257.
Kraft, R. P., 1957, Astrophys. J. 125, 336.
Kraft, R. P., Preston, G. W. and Wolff, S. C., 1964, Astrophys. J. 140, 235.
Kraft, R. P., 1967, IAU Symp. 28, p. 236.
Kron, G. E., 1947, Publ. astr. Soc. Pacific 59, 261.
Kron, G. E., 1952, Astrophys. J. 115, 301.
Kuhi, L. V., 1964, Astrophys. J. 140, 1408.
Kuhi, L. V., 1966, Stellar Evolution. Plenum Press New York, p. 373.
Kurochkin, N. E., 1962, Perem. Zvezdy 14, 284.
Kwee, K. K., 1967, Bull. astr. Inst. Netherl. Suppl. 2, 97.
Leighton, R. B., 1964, Astrophys. J. 140, 1120.
Liller, W., 1968, Astrophys. J. 151, 589.
Limber, D. N. and Marlborough, J. M., 1968, Astrophys. J. 152, 181.
Loreta, E., 1934, Astr. Nachr. 254, 151.
Lortet-Zuckermann, M. C., 1966, Ann. Astrophys. 29, 205.
Lovell, B., 1964, Observatory 84, 191.
Lukatskaya, F. I., 1966, Per. Zvezdy 16, 168.
Lukatskaya, F. I., 1968, Inf. Bul. Var. Stars No. 295. (IBVS N°.295)
Merrill, P. W., 1960, Stellar Atmospheres. The University of Chicago Press, p. 512.
O'Keefe, J. A., 1939, Astrophys. J. 90, 294.
Paczynski, B. and Ziólkowski, J., 1968, Acta Astr. 18, 255.
Penston, M. V., 1968, Inf. Bul. Var. Stars 255. (IBVS N°.255)
Preston, G. W., 1967, The Magnetic and Related Stars. Mono Book Corp. Baltimore, p. 3.
Schmitt, J. L., 1968, Nature 218, 663.
Serkowski, K., 1966a, Astrophys. J. 144, 857.
Serkowski, K., 1966b, Inf. Bul. Var. Stars No. 141. (IBVS N°.141)
Slee, O. B., Komesaroff, M. M. and McCullock, P. M., 1968, Nature 219, 342.
Sharpless, S., Riegel, K. and Williams, J. O., 1966, R. astr. Soc. Can. 60, 15.
Sterne, T. E., 1934, Harvard Bul. 896, 16 and 17.
Struve, O., 1931, Astrophys. J. 73, 94.
Szeidl, B., 1965, Mitt. Sternwarte Budapest No. 58 (CoKon N°.58)
Tsessevich, V. P. and Dragomirezkaya, B. A., 1967, Sky Tel. 34, 366.
Underhill, A. B., 1960, IAU Symp. No. 12, p. 88.
Vaughan, A. H. Jr., and Zirin, H., 1968, Astrophys. J. 152, 123.
Wallerstein, G. and Crampton, D., 1967, Astrophys. J. 149, 225.
Wallerstein, G., 1968(a), Astrophys. J. 151, 1011.
Wallerstein, G., 1968(b), Observatory 88, 111.
Weyman, R., 1962, Astrophys. J. 136, 476 and 844.
Wickramasinghe, N. C., 1968, Mon. Not. R. astr. Soc. 140, 273.
Wilson, O. C. and Bappu, M. K. Vainu, 1957, Astrophys. J. 125, 661.
Zhevakin, S. A., 1959, Astr. Zu. 36, 394.
Fig. 7. Light maxima and minima of RU Cam in V, according to photoelectric
observations obtained by Szeidl at the 24" reflector of the Konkoly Observatory.
I have only touched some few aspects of irregular stellar activity. Our
field is tremendous. From the theoretical side it comprises questions of
stellar stability, pulsation theory, turbulence and shock wave theory,
i.e., the dynamic theory of stellar envelopes, further, celestial
mechanics, magnetohydrodynamics and questions of stellar evolution. From
the observational side it extends over all periodic or non-periodic
variables, over intrinsic as well as eclipsing variables. Its complete
understanding postulates the knowledge of solar physics in highest
degree. And the reason for not yet proposing a symposium with solar
physicists, is because they would have a great advantage over us. We may
hope that not in the far future variable star astronomers will be able
to give the same help to solar physicists as they give at present to us.
REFERENCES
Ambarzumjan, V. A., 1954. Comm. Byurakan Obs. No. 13.
Ashbrook, J., Duncombe, R. L. and Van Woerkom, A. J. J., 1954, Astr. J. 59, 12.
Balázs-Detre, Julia and Detre, L., 1965, Kl. Veröff. Remeis-Sternw. Bamberg IV,
No. 40 p. 184.
Balázs-Detre, Julia, 1959, Kl. Veröff. Remeis-Sternw. Bamberg 27, 26.
Bonsack W. K. and Culver, R. B., 1966, Astrophys. J. 145, 767.
Christy, R. F., 1965, Kl. Veröff. Remeis-Sternw. Bamberg, 40, 77.
Crampin, J. and Hoyle, F., 1960, Mon. Not. R. astr. Soc. 120, 33.
Demers, S. and Crampton, D., 1966, Astr. J. 71, 852.
Demers, S. and Fernie, J. D., 1966, Astrophys. J. 144, 440.
Detre, L., 1966, Inf. Bul. Var. Stars No. 152. (IBVS N°.152)
Deutsch, A. J., 1956, Astrophys. J. 123, 210.
Deutsch, A. J., 1966, Stellar Evolution. Plenum Press New York p. 377.
Deutsch, A. J., 1967, IAU Circ. No. 2020.
Donn, B., Stecher, T. P., Wickramasinghe, N. C. and Williams, D. A., 1966, Astrophys.
J. 145, 949.
Durney, B. R., Faulkner, J., Gribbin, J. R. and Roxburgh, I. W., 1968, Nature 218, 20.
Epstein, J., 1950, Astrophys. J. 112, 6.
Faraggiana, R. and Hack, M., 1967, Z. Astrophys. 66, 343.
Godoli, G., 1967, Atti dell'XI. Convegno, Padova, p. 224.
Griffin, R. F., 1964, Observatory 83, 255.
Haro, G., 1967, Stars and Stellar Systems. Vol. VIII. 141.
Hazlehurst, J., 1967, Z. Astrophys. 65, 311.
Herbig, G. H., 1952, Astrophys. J. 116, 369.
Herbig, G. H., 1960, Astrophys. J. 132, 76.
Herbig, G. H., 1966, Vistas in Astr. 8, 109.
Herbig, G. H., Preston, G. W., Smak, J. and Paczynski, B., 1967, Astrophys. J. 141, 617.
Herbig, G. H., 1968. Inf. Bul. Var. Stars No. 243. (IBVS N°.243)
Jacobsen, T. S., 1960, Publ. Dom. Astrophys. Obs. Victoria 10, 145.
Jenkins, E. B. and Morton, D. C., 1967, Nature 215, 1257.
Kraft, R. P., 1957, Astrophys. J. 125, 336.
Kraft, R. P., Preston, G. W. and Wolff, S. C., 1964, Astrophys. J. 140, 235.
Kraft, R. P., 1967, IAU Symp. 28, p. 236.
Kron, G. E., 1947, Publ. astr. Soc. Pacific 59, 261.
Kron, G. E., 1952, Astrophys. J. 115, 301.
Kuhi, L. V., 1964, Astrophys. J. 140, 1408.
Kuhi, L. V., 1966, Stellar Evolution. Plenum Press New York, p. 373.
Kurochkin, N. E., 1962, Perem. Zvezdy 14, 284.
Kwee, K. K., 1967, Bull. astr. Inst. Netherl. Suppl. 2, 97.
Leighton, R. B., 1964, Astrophys. J. 140, 1120.
Liller, W., 1968, Astrophys. J. 151, 589.
Limber, D. N. and Marlborough, J. M., 1968, Astrophys. J. 152, 181.
Loreta, E., 1934, Astr. Nachr. 254, 151.
Lortet-Zuckermann, M. C., 1966, Ann. Astrophys. 29, 205.
Lovell, B., 1964, Observatory 84, 191.
Lukatskaya, F. I., 1966, Per. Zvezdy 16, 168.
Lukatskaya, F. I., 1968, Inf. Bul. Var. Stars No. 295. (IBVS N°.295)
Merrill, P. W., 1960, Stellar Atmospheres. The University of Chicago Press, p. 512.
O'Keefe, J. A., 1939, Astrophys. J. 90, 294.
Paczynski, B. and Ziólkowski, J., 1968, Acta Astr. 18, 255.
Penston, M. V., 1968, Inf. Bul. Var. Stars 255. (IBVS N°.255)
Preston, G. W., 1967, The Magnetic and Related Stars. Mono Book Corp. Baltimore, p. 3.
Schmitt, J. L., 1968, Nature 218, 663.
Serkowski, K., 1966a, Astrophys. J. 144, 857.
Serkowski, K., 1966b, Inf. Bul. Var. Stars No. 141. (IBVS N°.141)
Slee, O. B., Komesaroff, M. M. and McCullock, P. M., 1968, Nature 219, 342.
Sharpless, S., Riegel, K. and Williams, J. O., 1966, R. astr. Soc. Can. 60, 15.
Sterne, T. E., 1934, Harvard Bul. 896, 16 and 17.
Struve, O., 1931, Astrophys. J. 73, 94.
Szeidl, B., 1965, Mitt. Sternwarte Budapest No. 58 (CoKon N°.58)
Tsessevich, V. P. and Dragomirezkaya, B. A., 1967, Sky Tel. 34, 366.
Underhill, A. B., 1960, IAU Symp. No. 12, p. 88.
Vaughan, A. H. Jr., and Zirin, H., 1968, Astrophys. J. 152, 123.
Wallerstein, G. and Crampton, D., 1967, Astrophys. J. 149, 225.
Wallerstein, G., 1968(a), Astrophys. J. 151, 1011.
Wallerstein, G., 1968(b), Observatory 88, 111.
Weyman, R., 1962, Astrophys. J. 136, 476 and 844.
Wickramasinghe, N. C., 1968, Mon. Not. R. astr. Soc. 140, 273.
Wilson, O. C. and Bappu, M. K. Vainu, 1957, Astrophys. J. 125, 661.
Zhevakin, S. A., 1959, Astr. Zu. 36, 394.
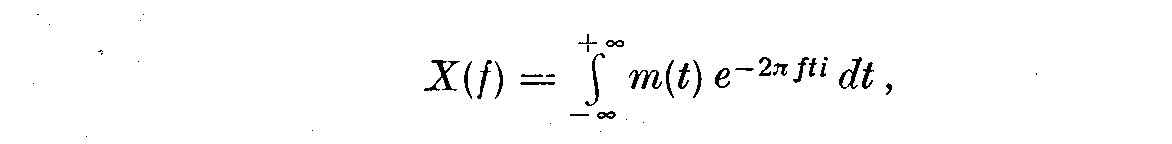 (1)
where m(t) is the light curve, X (f) is the Fourier spectrum.
We can consider irregular stellar variability as the observable effect
of random succession of transitory events. On the sun and some types of
variable stars, e.g. novae, U Geminorum, R Coronae Borealis and flare
stars, these events can be observed separately. Solar activity can be
followed even spatially separated. But generally, only the intermingling
of many local and global transitory events can be observed in the stars
as a continuously varying irregular light curve.
Also such a random time series m = m(t) can be represented by a
complicated mathematical relationship over a time interval (0, T). But
the formula will not hold for t > T. We obtain for different time
intervals different formulae, different sample records of the same
random process. Therefore, it is more practical to characterize a random
time series by some simple parameters:
1. Taking the mean value of m for a time interval (0, T)
(1)
where m(t) is the light curve, X (f) is the Fourier spectrum.
We can consider irregular stellar variability as the observable effect
of random succession of transitory events. On the sun and some types of
variable stars, e.g. novae, U Geminorum, R Coronae Borealis and flare
stars, these events can be observed separately. Solar activity can be
followed even spatially separated. But generally, only the intermingling
of many local and global transitory events can be observed in the stars
as a continuously varying irregular light curve.
Also such a random time series m = m(t) can be represented by a
complicated mathematical relationship over a time interval (0, T). But
the formula will not hold for t > T. We obtain for different time
intervals different formulae, different sample records of the same
random process. Therefore, it is more practical to characterize a random
time series by some simple parameters:
1. Taking the mean value of m for a time interval (0, T)
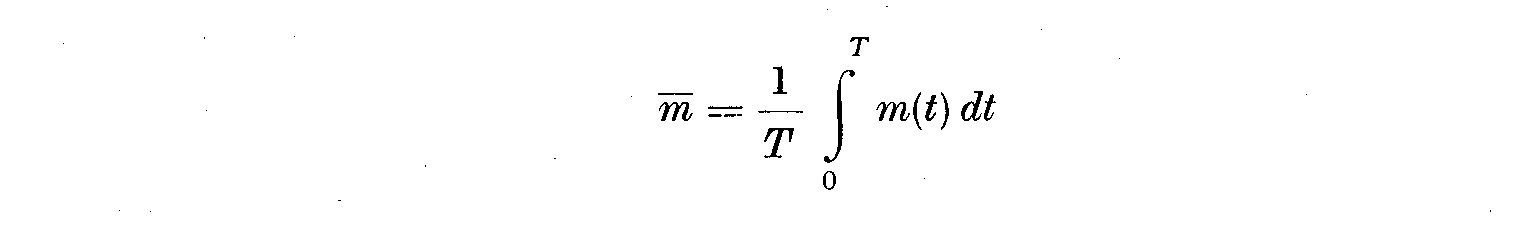 (2)
and putting mean(m) = 0 we can define the variance, as the mean square value
about the mean, by
(2)
and putting mean(m) = 0 we can define the variance, as the mean square value
about the mean, by
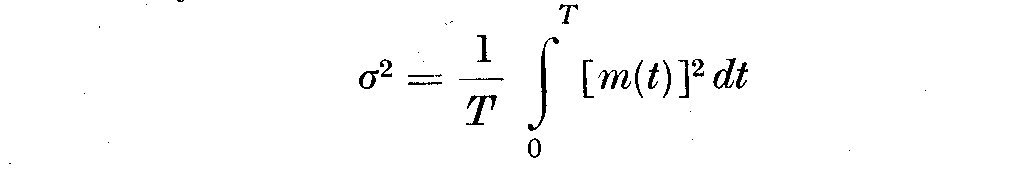 (3)
The positive square root of the variance is called the standard deviation.
2. The probability density function describes the probability that the
data will assume a value within some defined range at any instant of
time. The probability that m(t) assumes a value within the range between
m and m + Delta m may be obtained by taking the ratio T_(m, m + Delta m) / T ,
where T_(m, m + Delta m) is the total amount of time that m(t) falls inside
the range (m, m + Delta m) during an observation time T.
3. The autocorrelation function describes the general dependence of the
values of the data at one time on the values at another time. An
estimate for the autocorrelation between the values of m(t) at times t
and t + tau may be obtained by taking the product of the two values and
averaging over the observation time T. In equation form:
(3)
The positive square root of the variance is called the standard deviation.
2. The probability density function describes the probability that the
data will assume a value within some defined range at any instant of
time. The probability that m(t) assumes a value within the range between
m and m + Delta m may be obtained by taking the ratio T_(m, m + Delta m) / T ,
where T_(m, m + Delta m) is the total amount of time that m(t) falls inside
the range (m, m + Delta m) during an observation time T.
3. The autocorrelation function describes the general dependence of the
values of the data at one time on the values at another time. An
estimate for the autocorrelation between the values of m(t) at times t
and t + tau may be obtained by taking the product of the two values and
averaging over the observation time T. In equation form:
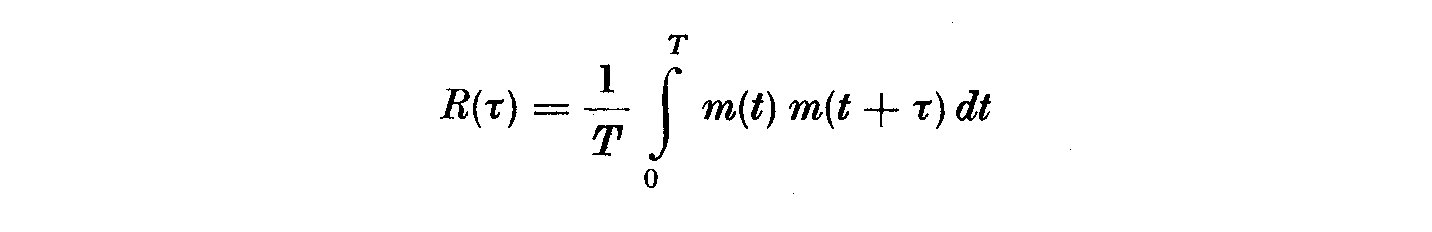 (4)
R(tau) is an even function with a maximum at tau = 0.
4. For stationary data, i.e. for data characterized by time-independent
parameters, we can construct the Fourier transform of the autocorrelation
function
(4)
R(tau) is an even function with a maximum at tau = 0.
4. For stationary data, i.e. for data characterized by time-independent
parameters, we can construct the Fourier transform of the autocorrelation
function
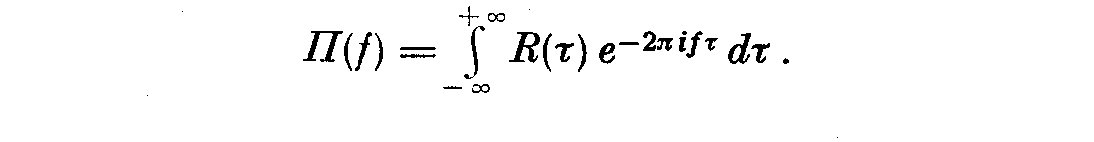 (5)
Pi(f) is called the power spectral density function. That is a breakdown of the
light curve into sinusoidal components and gives the mean squared amplitude
of each component.
In the first column of Fig. 1. we see four special light curves, a sine
wave (a), a sine wave with superposed irregularity (b), a narrow-band random
light curve having cycles of nearly equal length (c), and a wide-band random
light curve with strongly different cycles (d).
In the next column of Fig. 1. we see the corresponding probability density
function plots. For the sine wave we have the maxima for p(m) at the
extremities, because the curve varies slowly there.
Next to the right we see the autocorrelograms. The sharply
peaked autocorrelogram diminishing rapidly to zero (d) is typical of
wide-band random data with a zero mean value. The autocorrelogram for
the sine wave with random noise is simply the sum of the
autocorrelograms for the sine wave and random noise separately (b). On
the other hand, the autocorrelogram for the narrow-band random light
curve appears like a decaying version of a sine wave autocorrelogram.
Finally we see the corresponding power spectra. A discrete power
spectrum for a sine wave and a relatively smooth and broad power
spectrum for the wide-band random light curve. The power spectrum for
the sine wave with irregularities is the sum of the power spectra for
the sine wave and the random case separately. On the other hand, the
power spectra for the narrow band random light curve is sharply peaked,
but still smoothly continuous as for random light-curve. The period
corresponding to the peak may be called as pseudo-period. The four
examples illustrate a definite trend in all the three parameters going
from the sine wave to the wide-band noise case.
The principal application for an autocorrelation and for a power spectral
density function is the detection of periodicities which might be masked in a
random background. Any periodicity in the light variation will manifest
itself as a series of peaks corresponding to a fundamental and its
harmonics.
Such method of analysis requires enormous amount of computation,
hence it has not been popular in the past. With the aid of high speed
computers this is no longer a problem. However, the requirements
of accuracy, extent, continuity, and reasonable homogeneity for the light
curve to be analysed restrict considerably the applicability of the method
to semiregular or irregular variable stars. Only one single semiregular
variable was till now treated by this way, mu Cephei, on the one hand
by Ashbrook, Duncombe and Woerkom (1954), who found the light curve to result
from stochastic rather than harmonic processes, on the other hand by Sharpless,
Riegel and Williams (1966) with the conclusion that the light variations are
characterized by a much greater degree of regularity than is generally
attributed to stars classed as semiregular variables.
(5)
Pi(f) is called the power spectral density function. That is a breakdown of the
light curve into sinusoidal components and gives the mean squared amplitude
of each component.
In the first column of Fig. 1. we see four special light curves, a sine
wave (a), a sine wave with superposed irregularity (b), a narrow-band random
light curve having cycles of nearly equal length (c), and a wide-band random
light curve with strongly different cycles (d).
In the next column of Fig. 1. we see the corresponding probability density
function plots. For the sine wave we have the maxima for p(m) at the
extremities, because the curve varies slowly there.
Next to the right we see the autocorrelograms. The sharply
peaked autocorrelogram diminishing rapidly to zero (d) is typical of
wide-band random data with a zero mean value. The autocorrelogram for
the sine wave with random noise is simply the sum of the
autocorrelograms for the sine wave and random noise separately (b). On
the other hand, the autocorrelogram for the narrow-band random light
curve appears like a decaying version of a sine wave autocorrelogram.
Finally we see the corresponding power spectra. A discrete power
spectrum for a sine wave and a relatively smooth and broad power
spectrum for the wide-band random light curve. The power spectrum for
the sine wave with irregularities is the sum of the power spectra for
the sine wave and the random case separately. On the other hand, the
power spectra for the narrow band random light curve is sharply peaked,
but still smoothly continuous as for random light-curve. The period
corresponding to the peak may be called as pseudo-period. The four
examples illustrate a definite trend in all the three parameters going
from the sine wave to the wide-band noise case.
The principal application for an autocorrelation and for a power spectral
density function is the detection of periodicities which might be masked in a
random background. Any periodicity in the light variation will manifest
itself as a series of peaks corresponding to a fundamental and its
harmonics.
Such method of analysis requires enormous amount of computation,
hence it has not been popular in the past. With the aid of high speed
computers this is no longer a problem. However, the requirements
of accuracy, extent, continuity, and reasonable homogeneity for the light
curve to be analysed restrict considerably the applicability of the method
to semiregular or irregular variable stars. Only one single semiregular
variable was till now treated by this way, mu Cephei, on the one hand
by Ashbrook, Duncombe and Woerkom (1954), who found the light curve to result
from stochastic rather than harmonic processes, on the other hand by Sharpless,
Riegel and Williams (1966) with the conclusion that the light variations are
characterized by a much greater degree of regularity than is generally
attributed to stars classed as semiregular variables.
 Fig. 1. Light curves, corresponding probability density functions,
autocorrelograms and power spectra (s. text).
Lukatskaya (1966) has investigated the autocorrelation and spectral functions
of seven T Tauri-type variables and those of AE Aqr (1968), Kurochkin (1962)
those of T Orionis, and on this colloquium we shall hear Dr. Plagemann
on the same topic.
A very important question is, are the parameters of the light curves of
irregular variables constant in time, or are they changing. Tsessevitch and
Dragomineskaya (1967) investigated the light variation of 10 RW Aurigae stars
on sky patrol photographs of the Odessa, Harvard, Dushanbe and Sonneberg
observatories. They prepared probability density functions for several stars,
finding longterm variations of this function, with cycles of 25 to 60 years.
Hence, light curves of some irregular variables represent nonstationary data.
A particular random process is the so called Markov process. The property
that distinguishes Markov processes from more general random ones can be
described in non-mathematical form like this: If we know the present state of
the process, and want to make predictions about its future, then information
about the past has no predictive value, i.e. the process has no memory, its
relationship to the past does not extend beyond the immediately preceding
observation. We have a beautiful example for Markov processes in astronomy,
the O-C diagrams for periodic variables, if the period or phase fluctuations
are random, and independent from the preceding ones.
If we are able to determine the length of many individual cycles of a
variable star, as for example in the case of continuously observed
Mira-variables, we can test directly whether successive periods fluctuate
accidentally or not. Moreover we can also determine the probability
density function of the phase-fluctuations: psi(f). For cepheids,
eclipsing binaries and every kind of short-period variables we must get
every information for period-changes from the study of O-C diagrams.
These are for most types of periodic variables determined by the
cumulative effects of random phase fluctuations. At the Bamberg
Colloquium we have shown how the probability structure of the O-C
diagram could be determined using the central limit theorem of
probability theory (Balázs-Detre and Detre, 1965). The structure depends
on the mean square value of the phase fluctuations, sigma, where
Fig. 1. Light curves, corresponding probability density functions,
autocorrelograms and power spectra (s. text).
Lukatskaya (1966) has investigated the autocorrelation and spectral functions
of seven T Tauri-type variables and those of AE Aqr (1968), Kurochkin (1962)
those of T Orionis, and on this colloquium we shall hear Dr. Plagemann
on the same topic.
A very important question is, are the parameters of the light curves of
irregular variables constant in time, or are they changing. Tsessevitch and
Dragomineskaya (1967) investigated the light variation of 10 RW Aurigae stars
on sky patrol photographs of the Odessa, Harvard, Dushanbe and Sonneberg
observatories. They prepared probability density functions for several stars,
finding longterm variations of this function, with cycles of 25 to 60 years.
Hence, light curves of some irregular variables represent nonstationary data.
A particular random process is the so called Markov process. The property
that distinguishes Markov processes from more general random ones can be
described in non-mathematical form like this: If we know the present state of
the process, and want to make predictions about its future, then information
about the past has no predictive value, i.e. the process has no memory, its
relationship to the past does not extend beyond the immediately preceding
observation. We have a beautiful example for Markov processes in astronomy,
the O-C diagrams for periodic variables, if the period or phase fluctuations
are random, and independent from the preceding ones.
If we are able to determine the length of many individual cycles of a
variable star, as for example in the case of continuously observed
Mira-variables, we can test directly whether successive periods fluctuate
accidentally or not. Moreover we can also determine the probability
density function of the phase-fluctuations: psi(f). For cepheids,
eclipsing binaries and every kind of short-period variables we must get
every information for period-changes from the study of O-C diagrams.
These are for most types of periodic variables determined by the
cumulative effects of random phase fluctuations. At the Bamberg
Colloquium we have shown how the probability structure of the O-C
diagram could be determined using the central limit theorem of
probability theory (Balázs-Detre and Detre, 1965). The structure depends
on the mean square value of the phase fluctuations, sigma, where
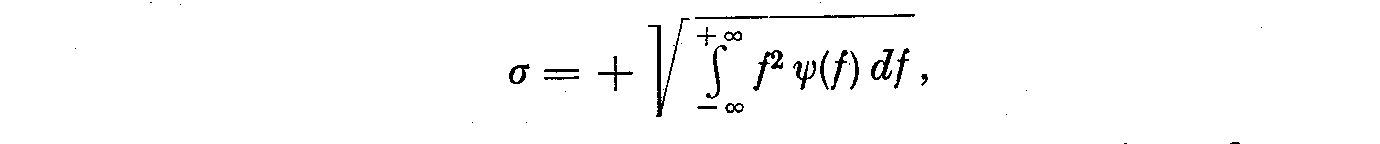 (6)
but it is highly independent from psi(f). O-C diagrams resulting from random
phase-fluctuations consist of cycles of different lengths and amplitudes.
(See Fig. 2, showing the O-C diagrams of three W Virginis-type variables:
RU Cam, AP Herculis and kappa Pavonis.)
(6)
but it is highly independent from psi(f). O-C diagrams resulting from random
phase-fluctuations consist of cycles of different lengths and amplitudes.
(See Fig. 2, showing the O-C diagrams of three W Virginis-type variables:
RU Cam, AP Herculis and kappa Pavonis.)
 Fig. 2. O-C diagrams for three W Virginis-type variables, RU Cam,
AP Her and kappa Pav. That for AP Her is taken from Kwee (1967). For RU
Cam, the strongly oscillating phase corresponds to the recent
semiregular behaviour of the star.
Till now we have no evidence of evolutionary period-changes for most
kinds of variables. Some cyclic terms in the O-C diagrams can be interpreted
as due to binary or apsidal motion, but generally they must be treated as
cumulative effects of random fluctuations. The value of sigma can be
determined from the O-C diagrams.
Several attempts have been made to represent the time sequence of explosions
of eruptive variables by a Markov chain. Yet, as Mme Lortet-Zuckermann (1966)
has stated, the Markov chain seemed poorly adapted for the representation
of the sequence of the various sorts of explosions of the SS Cygni stars.
Stellar variability refuses compliance with simple mathematical models.
The maxima or minima of an ideally irregular variable would be distributed
at random, and the cycle lengths l would follow a Poisson-distribution:
Fig. 2. O-C diagrams for three W Virginis-type variables, RU Cam,
AP Her and kappa Pav. That for AP Her is taken from Kwee (1967). For RU
Cam, the strongly oscillating phase corresponds to the recent
semiregular behaviour of the star.
Till now we have no evidence of evolutionary period-changes for most
kinds of variables. Some cyclic terms in the O-C diagrams can be interpreted
as due to binary or apsidal motion, but generally they must be treated as
cumulative effects of random fluctuations. The value of sigma can be
determined from the O-C diagrams.
Several attempts have been made to represent the time sequence of explosions
of eruptive variables by a Markov chain. Yet, as Mme Lortet-Zuckermann (1966)
has stated, the Markov chain seemed poorly adapted for the representation
of the sequence of the various sorts of explosions of the SS Cygni stars.
Stellar variability refuses compliance with simple mathematical models.
The maxima or minima of an ideally irregular variable would be distributed
at random, and the cycle lengths l would follow a Poisson-distribution:
 (7)
Sterne (1934) has shown that the minima of R Coronae Borealis fulfill
this condition. But this conclusion is only true if the minima are
independent events, and this is certainly not the case, if the minima
are not well separated.
We see that all analyses of this kind, with the exception of the search
of hidden periodicities or changes of the statistical parameters in
time, are rather formal and do not say much about the physical nature of
the stars, since objects of the most various kinds may show similar
light curves. Combined spectroscopic and photometric, sometimes radio
observations are needed to reveal the real nature of some objects with
irregular light variation. Such combined efforts often lead to
surprising results. I mention the beautiful interpretation of V Sagittae
by Herbig, Preston, Smak and Paczynski (1965), who resolved the complex
light variations of this star into three apparently independent
activities, showing that the star is a peculiar nova-like eclipsing
binary. VV Puppis, a star formerly classified as an RR Lyrae variable,
was interpreted by Herbig (1960) likewise as a nova-like double star. In
June 1967 Deutsch (1967) has reported that the spectrum of CH Cygni,
classified earlier as a semiregular a-type variable, changed from a
normal M6 type into that of a symbiotic nova-like star. The star now
shows rapid light variations in the ultraviolet (Wallerstein 1968b).
Using new high quality spectrograms, Herbig (1966) succeeded in
interpreting the 1936 flare-up of Wachmann's star, FU Orionis, as a
phenomenon of early stellar evolution, a pre-main-sequence collapse in
conformity with Hayashi and Cameron's ideas of early stellar evolution.
Two irregular variables have recently been identified as radio sources:
BW Tauri by Penston (1968) and BL Lacertae by Schmitt (1968)*.
* BW Tau = 3C120, BL Lac = VRO 42.22.01.
These examples go to show that we need in many cases special
interpretations for individual objects. Yet, we also have some general
principles for trying the physical interpretation of broad classes of
non-periodic phenomena in variable stars. These attempts can be
classified into four categories:
1. Solar analogies. An increasing convergence is apparent between the
fields of stellar physics and solar physics, stellar analogues of solar
phenomena are becoming the subjects of specific researches. I mention a
recent interesting paper by Godoli (1967) at the Padova 1967 conference.
2. Irregular phenomena connected with or caused by the binary nature of
the star, as eruptions of different kinds or other irregularities
associated with gaseous material streaming between the components in
very short-period binaries and in symbiotic variables, further, period
variations in all kinds of eclipsing and spectroscopic binaries.
3. Irregularities connected with rotational instability of the
equatorial region of a rapidly rotating star, as in Be, Of and
Wolf-Rayet stars.
4. Veiling theories, put forward by Merrill for long-period variables*
and considered by Loreta (1934) and O'Keefe (1939) in connection with R
Coronae Borealis in terms of solid carbon particles.
* Merrill, P. W., Stellar atmospheres. The University of Chicago Press
1960. p. 512.
The closest similarity between solar activity and irregular light
variation in stars is that between solar flares and extremely sudden
increases in the integrated brightness of some stars, mainly of flare
and T Tau stars. Since Sir Lovell (1964) discovered that optical stellar
flares are accompanied by radio bursts of the I, II and III solar type,
it became very probable that flare stars show in a gigantic form the
same kind of activity as the sun. The quite irregular light curve of
T Tauri stars could be due to the superposition of very many flares,
with a variation of the activity of the star, intermingled with effects
of the neighbouring circumstellar material. We shall have introductory
papers on this theme by Wenzel and Gershberg. I refer to a recent
excellent review on flare stars by Haro (1967). Since the Prague meeting
of the IAU, Commission 27 has under Chugainov's leadership a very well
organized working group on UV Ceti type stars for cooperative radio and
optical observations.
One of the most interesting possibilities for solar analogies is the
extension of our concept of the chromosphere and of its activity to stars.
The discovery of the Wilson-Bappu (1957) effect, a correlation over a range of
nearly 16 absolute magnitudes between the widths (and not the intensity)
of the emission cores of the H and K-lines of Calcium II and the visual
absolute magnitude for stars of types G, K and M, has engendered considerable
effort to interpret this effect in terms of chromospheric macroturbulence
including all irregular, non-periodic or pseudo-periodic motions of the atoms
in a stellar atmosphere. Kraft, Preston and Wolff (1964) showed that a similar
correlation exists between the width of the hydrogen (H_alpha) absorption line
and the ultraviolet absolute magnitude. Recently Vaughan and Zirin (1968)
studied the infrared He line at lambda 10830 A which is the only line from 3000
to 11 000 A that originates solely in the chromosphere, free of changes in an
underlying photospheric line. Since the line is excited only at high temperatures,
its presence is an excellent test for hot chromospheres in late-type stars.
The sun fits the Wilson-Bappu relation, but the intensity of K_2 emission
in the integrated light of the sun is very small and can be observed with high
dispersion only. In the spectra of many stars K_2 emission is observable even
with rather small dispersion, indicating that some stars possess much more
active chromospheres than does the sun.
Leighton (1964) has shown that the K_2 emission on the sun occurs at
the edge of supergranulation cells, where photospheric magnetic fields
are sometimes found to be strengthened to the order of 100 gauss. There
is a point-to-point correlation between chromospheric activity and the
photospheric magnetic field strength. The Ca II network is not due to a
circulation of matter in the chromosphere but due to a more general
circulation which underlies the chromosphere. To the same effect points
Bonsack and Culver's (1966) result that in K-type stars the widths of
weak lines which do not have a chromospheric origin, are well correlated
with the widths of K_2 emission or the strength of the infrared He-line.
Because this emission and the strength of the infrared He-line appear
greatly enhanced in the region of solar plages and in this way it is well
correlated with the 11-year solar cycle, a study of the nature of variability
of the K_2 emission or of the He-line in other, stars should add substantially
to our understanding of both sun and stars.
That K_2 does indeed vary, has been established by Wilson and Bappu, by
Griffin (1964), Deutsch, Vaughan, and most recently by Liller (1968),
especially in the stars alpha Bootis, alpha Tauri and epsilon Geminorum. The
type of variation noted has usually been a change in the relative intensities
of the violet and red components of the K_2 emission, but there was little
evidence of periodicity analogue to the solar cycle.
Transitory Ca II emission develops at the phase of minimum radius in
cepheids and longperiod variables. The study of this phenomenon by
Herbig (1952), Jacobsen (1956) and Kraft (1957) led Kraft (1967) at the
IAU Symposium 28 to the interesting suggestion, that the behaviour of
cepheids at this phase is an exaggeration of the disturbed sun. At the
time of minimum radius the surface of the cepheids becomes covered with
something like plages. As the cycle progresses, a shock wave moves
through the atmosphere and all such solar-like disturbances disappear:
the cepheid becomes an F-type star.
Some non-periodic secondary variations in eclipsing binaries were
attributed to star spots (Kron, 1947, 1952). But these stars are not
adapted for such investigations, because gas streams between and around
the components may cause irregularities in the light curve.
Prominence activity was found in supergiant stars, for example in 31
Cygni, which are components of eclipsing systems. When the star goes
behind the atmosphere of the supergiant K3 star, at times several
absorption components due to Calcium II H and K are seen, providing
unmistakable evidence that bodies of gas moving with discrete velocities
exist in its atmosphere (S. Underhill, 1960).
Mass loss in stars might bear a relation to the solar wind, which is a
plasma extension of the solar corona moving outward at the velocity of
about 500 km/sec carrying away a mass of about 10^-13 solar mass per year
and the frozen-in magnetic fields from the sun. The solar wind has a
steady continuous and an irregularly varying component. The evidence
that considerable mass loss occurs in stars apart from novae,
supernovae and close binaries, came from Deutsch's (1956) remarkable
discovery of a set of circumstellar lines in the visual companion of the
M supergiant alpha Herculis. There is now ample spectroscopic evidence for
the efflux of cool gas from the surfaces of all giant stars
with spectral types later than M0 (Deutsch, 1966), at a rate of some
10^-9 solar mass per year. Weyman (1962) pointed out the difficulties in
the way of a solar wind explanation for these phenomena. More violent
mass losses from stars are certainly not of the solar wind type. In some
pulsating stars the pulsation shock can be so violent that the surface
layer may be driven away from the star in a relatively small number of
periods, as was shown by Christy (1965) for W Virginis stars. According
to Paczynski and Ziólkowski (1968) Mira type variables may throw out
their envelopes and in this way planetary nebulae might be formed. Mass
loss may be the dominating factor in horizontal branch evolution rather
than nuclear burning. Kuhi (1964, 1966) estimated the rate of mass loss
from T Tauri stars at about 10^-7 solar mass per year. Spectra secured
from rocket flights provided first evidence for the extremely violent
ejection processes in the atmospheres of O and B-type supergiants and
bright giants (Jenkins and Morton, 1967). We shall hear more on this
subject next week in Trieste, where a Colloquium will be held on mass
loss from stars.
The weak point of solar analogies is that solar phenomena are not yet
quite understood. Yet, we can be certain of the magnetic nature of all
processes of solar activity and that all its accompanying phenomena like
spots, faculae, flares, the irregular component of solar wind, etc. are
connected with local concentration as well as annihilation of magnetic
fields. Hence it is very probable that also the analogous stellar
phenomena are of magnetic origin.
Moreover, it becomes increasingly evident that magnetic fields may have
a share also in other aspects of stellar irregularities. E.g., Merrill's
veiling theory is supported by Serkowski's (1966a, b) recent discovery
of large amounts of plane polarization in some Mira stars at minimum
light. This polarization can be explained by graphite flakes, condensed
in the atmosphere of these stars, presuming that they are aligned by
stellar magnetic fields (Donn et al. 1966; Wickramasinghe 1968).
Magnetic forces may play an important role in the formation of the
envelopes of Be stars. Of course, Struve's (1931) suggestion of
rotationally forced ejection in a star rotating at the rotational limit
in which its equatorial rotational velocity is first sufficient to
balance by centrifugal effects the gravitational attraction of the star
at its equator, is correct. But an additional force is required to move
the matter outward from the region just above the star's equator. The
complex kinematic behaviour of the shell, the occurrence of stars such
as Pleione, which seem able to lose and reform their shell at intervals,
is particularly suggestive of the presence of forces which trend to
drive the gases away from the star. Even quite weak magnetic fields
could produce significant dynamical effects in such a shell (Crampin and
Hoyle 1960; Limber and Marlborough 1968). Hazlehurst (1967) studied in a
recent paper the magnetic release of a circumstellar ring, and he found
that the gases describe a decelerated motion, compatible with the
observed spectral properties of circumstellar shells. From the ultimate
velocity of the material an observational determination of the magnetic
field in the stellar photosphere will be possible.*
* About problems of irregular variations in light and radial velocity of
Be, Of and WR stars I refer to the excellent book The Early Type Stars
by Anne B. Underhill (Reidel Publishing Company, 1966).
We would have a better understanding of the observed period-variations
in eclipsing binaries, if an adequate electromagnetic theory of the gaseous
streams in the systems had been elaborated. It appears from the work by
Plavec and Schneller that the most erratic O-C diagrams are obtained for
contact and undetached systems. If an O-C diagram has random walk
properties, then the underlying physical processes that give rise to
the random period fluctuations, are themselves random processes. Wood's
hypothesis of mass ejection for the explanation of the period
fluctuations, if the areas of ejection are distributed over the surface
at random, fits the criterion of randomness, but the required masses are
too high. However, we might have a very efficient agent for angular
momentum changes in the interaction of the ionized gaseous streams
moving around the components with the magnetic fields of the stars.
Magnetic fields might play an even greater role in hot short-period
eruptive binaries and in symbiotic stars. Babcock measured a magnetic field
of 1000 gauss in the symbiotic variable AG Pegasi. The configuration in
eruptive binaries, a highly ionized disk, a strongly flickering hot component
ejecting highly ionized material into the disk, might be extremely unstable,
especially if the components have strong magnetic fields. It is just possible
that the magnetic and gravitational instability of such a configuration might
lead from time to time to major eruptions. According to my opinion the seat of
the eruptions might be the plasma surrounding the stars, not a stellar
component.
According to Ambarzumjan's (1954) hypothesis, the continuous emission
observed in the spectra of the T Tauri type variables and UV Ceti type
stars during their outbursts originates from relativistic electrons in
the magnetic fields of these stars.
Random processes may influence the pulsation of the stars, giving rise
to irregular fluctuations in the light and radial velocity curve and in
the period. The triggering mechanism of the pulsation, which is sought
in the convective layers of the stars, may especially be sensitive to
magnetic activity.
Epstein (1950) has shown in an important paper that in highly centrally
concentrated stellar models the period of the fundamental mode is
determined primarily by conditions in the envelope and that the period
is almost independent of conditions in the central regions where most of
the mass is located. This result suggests that stellar pulsation, at
least in giant and supergiant-like stars, is a fairly superficial
phenomenon effecting only the outer stellar layers. The higher modes are
even more sensitive to properties of the most external layers of the
star, since these modes have higher relative amplitudes near the
surface.
Indeed, red variables, where the outer layers play a great role, have
very erratic light variation, whereas classical Cepheids and most RR
Lyrae stars show very little if any irregularities.
Zhevakin introduced the peripheral zone of He II critical ionization
as the excitation mechanism of the pulsation. He (1959) developed an
interesting theory of semiregular and irregular variables. The period of
oscillation of the inner region of the star is constant to a high degree
of accuracy. The nonadiabatic oscillations of the atmosphere show
relative to the adiabatic oscillations of the inner regions a phase
shift, whose value depends primarily on how close is the ionization zone
to the stellar surface. Random fluctuations in the position of the zone
change the phase shift, and in this way the period of the outer zones
will fluctuate about the period of oscillations of the inner region.
If the driving mechanism of the pulsation is affected by random
perturbations, wee may expect a suppression of the amplitude of the
pulsation relative to stars free from such perturbations. As it is well
known, semiregular red variables differ from the longperiod variables
only in their smaller amplitudes (Fig. 3).
The RR Lyrae-variables with the Blashko-effect have very complicated
O-C diagrams. Though the Blashko-effect is a periodic phenomenon, it
causes great random fluctuations both in the fundamental and in the
secondary period (Fig. 4). As a period-amplitude diagram for RRab-stars
in M3, taken from a paper by Szeidl (1965), shows (Fig. 5), the mean
amplitudes of the RRab stars with Blashko-effect are much smaller than
the amplitudes of RRab stars with stable light curves.
Babcock discovered a strongly variable, magnetic field in RR Lyrae
which ranges from +1200 to -1600 gauss. Julia Balázs (1959) has shown
that there was some correlation between Babcock's measures and the
Blashko-effect of this star: the maximum positive and maximum negative
fields were associated with the maximum and minimum light amplitudes,
respectively.
(7)
Sterne (1934) has shown that the minima of R Coronae Borealis fulfill
this condition. But this conclusion is only true if the minima are
independent events, and this is certainly not the case, if the minima
are not well separated.
We see that all analyses of this kind, with the exception of the search
of hidden periodicities or changes of the statistical parameters in
time, are rather formal and do not say much about the physical nature of
the stars, since objects of the most various kinds may show similar
light curves. Combined spectroscopic and photometric, sometimes radio
observations are needed to reveal the real nature of some objects with
irregular light variation. Such combined efforts often lead to
surprising results. I mention the beautiful interpretation of V Sagittae
by Herbig, Preston, Smak and Paczynski (1965), who resolved the complex
light variations of this star into three apparently independent
activities, showing that the star is a peculiar nova-like eclipsing
binary. VV Puppis, a star formerly classified as an RR Lyrae variable,
was interpreted by Herbig (1960) likewise as a nova-like double star. In
June 1967 Deutsch (1967) has reported that the spectrum of CH Cygni,
classified earlier as a semiregular a-type variable, changed from a
normal M6 type into that of a symbiotic nova-like star. The star now
shows rapid light variations in the ultraviolet (Wallerstein 1968b).
Using new high quality spectrograms, Herbig (1966) succeeded in
interpreting the 1936 flare-up of Wachmann's star, FU Orionis, as a
phenomenon of early stellar evolution, a pre-main-sequence collapse in
conformity with Hayashi and Cameron's ideas of early stellar evolution.
Two irregular variables have recently been identified as radio sources:
BW Tauri by Penston (1968) and BL Lacertae by Schmitt (1968)*.
* BW Tau = 3C120, BL Lac = VRO 42.22.01.
These examples go to show that we need in many cases special
interpretations for individual objects. Yet, we also have some general
principles for trying the physical interpretation of broad classes of
non-periodic phenomena in variable stars. These attempts can be
classified into four categories:
1. Solar analogies. An increasing convergence is apparent between the
fields of stellar physics and solar physics, stellar analogues of solar
phenomena are becoming the subjects of specific researches. I mention a
recent interesting paper by Godoli (1967) at the Padova 1967 conference.
2. Irregular phenomena connected with or caused by the binary nature of
the star, as eruptions of different kinds or other irregularities
associated with gaseous material streaming between the components in
very short-period binaries and in symbiotic variables, further, period
variations in all kinds of eclipsing and spectroscopic binaries.
3. Irregularities connected with rotational instability of the
equatorial region of a rapidly rotating star, as in Be, Of and
Wolf-Rayet stars.
4. Veiling theories, put forward by Merrill for long-period variables*
and considered by Loreta (1934) and O'Keefe (1939) in connection with R
Coronae Borealis in terms of solid carbon particles.
* Merrill, P. W., Stellar atmospheres. The University of Chicago Press
1960. p. 512.
The closest similarity between solar activity and irregular light
variation in stars is that between solar flares and extremely sudden
increases in the integrated brightness of some stars, mainly of flare
and T Tau stars. Since Sir Lovell (1964) discovered that optical stellar
flares are accompanied by radio bursts of the I, II and III solar type,
it became very probable that flare stars show in a gigantic form the
same kind of activity as the sun. The quite irregular light curve of
T Tauri stars could be due to the superposition of very many flares,
with a variation of the activity of the star, intermingled with effects
of the neighbouring circumstellar material. We shall have introductory
papers on this theme by Wenzel and Gershberg. I refer to a recent
excellent review on flare stars by Haro (1967). Since the Prague meeting
of the IAU, Commission 27 has under Chugainov's leadership a very well
organized working group on UV Ceti type stars for cooperative radio and
optical observations.
One of the most interesting possibilities for solar analogies is the
extension of our concept of the chromosphere and of its activity to stars.
The discovery of the Wilson-Bappu (1957) effect, a correlation over a range of
nearly 16 absolute magnitudes between the widths (and not the intensity)
of the emission cores of the H and K-lines of Calcium II and the visual
absolute magnitude for stars of types G, K and M, has engendered considerable
effort to interpret this effect in terms of chromospheric macroturbulence
including all irregular, non-periodic or pseudo-periodic motions of the atoms
in a stellar atmosphere. Kraft, Preston and Wolff (1964) showed that a similar
correlation exists between the width of the hydrogen (H_alpha) absorption line
and the ultraviolet absolute magnitude. Recently Vaughan and Zirin (1968)
studied the infrared He line at lambda 10830 A which is the only line from 3000
to 11 000 A that originates solely in the chromosphere, free of changes in an
underlying photospheric line. Since the line is excited only at high temperatures,
its presence is an excellent test for hot chromospheres in late-type stars.
The sun fits the Wilson-Bappu relation, but the intensity of K_2 emission
in the integrated light of the sun is very small and can be observed with high
dispersion only. In the spectra of many stars K_2 emission is observable even
with rather small dispersion, indicating that some stars possess much more
active chromospheres than does the sun.
Leighton (1964) has shown that the K_2 emission on the sun occurs at
the edge of supergranulation cells, where photospheric magnetic fields
are sometimes found to be strengthened to the order of 100 gauss. There
is a point-to-point correlation between chromospheric activity and the
photospheric magnetic field strength. The Ca II network is not due to a
circulation of matter in the chromosphere but due to a more general
circulation which underlies the chromosphere. To the same effect points
Bonsack and Culver's (1966) result that in K-type stars the widths of
weak lines which do not have a chromospheric origin, are well correlated
with the widths of K_2 emission or the strength of the infrared He-line.
Because this emission and the strength of the infrared He-line appear
greatly enhanced in the region of solar plages and in this way it is well
correlated with the 11-year solar cycle, a study of the nature of variability
of the K_2 emission or of the He-line in other, stars should add substantially
to our understanding of both sun and stars.
That K_2 does indeed vary, has been established by Wilson and Bappu, by
Griffin (1964), Deutsch, Vaughan, and most recently by Liller (1968),
especially in the stars alpha Bootis, alpha Tauri and epsilon Geminorum. The
type of variation noted has usually been a change in the relative intensities
of the violet and red components of the K_2 emission, but there was little
evidence of periodicity analogue to the solar cycle.
Transitory Ca II emission develops at the phase of minimum radius in
cepheids and longperiod variables. The study of this phenomenon by
Herbig (1952), Jacobsen (1956) and Kraft (1957) led Kraft (1967) at the
IAU Symposium 28 to the interesting suggestion, that the behaviour of
cepheids at this phase is an exaggeration of the disturbed sun. At the
time of minimum radius the surface of the cepheids becomes covered with
something like plages. As the cycle progresses, a shock wave moves
through the atmosphere and all such solar-like disturbances disappear:
the cepheid becomes an F-type star.
Some non-periodic secondary variations in eclipsing binaries were
attributed to star spots (Kron, 1947, 1952). But these stars are not
adapted for such investigations, because gas streams between and around
the components may cause irregularities in the light curve.
Prominence activity was found in supergiant stars, for example in 31
Cygni, which are components of eclipsing systems. When the star goes
behind the atmosphere of the supergiant K3 star, at times several
absorption components due to Calcium II H and K are seen, providing
unmistakable evidence that bodies of gas moving with discrete velocities
exist in its atmosphere (S. Underhill, 1960).
Mass loss in stars might bear a relation to the solar wind, which is a
plasma extension of the solar corona moving outward at the velocity of
about 500 km/sec carrying away a mass of about 10^-13 solar mass per year
and the frozen-in magnetic fields from the sun. The solar wind has a
steady continuous and an irregularly varying component. The evidence
that considerable mass loss occurs in stars apart from novae,
supernovae and close binaries, came from Deutsch's (1956) remarkable
discovery of a set of circumstellar lines in the visual companion of the
M supergiant alpha Herculis. There is now ample spectroscopic evidence for
the efflux of cool gas from the surfaces of all giant stars
with spectral types later than M0 (Deutsch, 1966), at a rate of some
10^-9 solar mass per year. Weyman (1962) pointed out the difficulties in
the way of a solar wind explanation for these phenomena. More violent
mass losses from stars are certainly not of the solar wind type. In some
pulsating stars the pulsation shock can be so violent that the surface
layer may be driven away from the star in a relatively small number of
periods, as was shown by Christy (1965) for W Virginis stars. According
to Paczynski and Ziólkowski (1968) Mira type variables may throw out
their envelopes and in this way planetary nebulae might be formed. Mass
loss may be the dominating factor in horizontal branch evolution rather
than nuclear burning. Kuhi (1964, 1966) estimated the rate of mass loss
from T Tauri stars at about 10^-7 solar mass per year. Spectra secured
from rocket flights provided first evidence for the extremely violent
ejection processes in the atmospheres of O and B-type supergiants and
bright giants (Jenkins and Morton, 1967). We shall hear more on this
subject next week in Trieste, where a Colloquium will be held on mass
loss from stars.
The weak point of solar analogies is that solar phenomena are not yet
quite understood. Yet, we can be certain of the magnetic nature of all
processes of solar activity and that all its accompanying phenomena like
spots, faculae, flares, the irregular component of solar wind, etc. are
connected with local concentration as well as annihilation of magnetic
fields. Hence it is very probable that also the analogous stellar
phenomena are of magnetic origin.
Moreover, it becomes increasingly evident that magnetic fields may have
a share also in other aspects of stellar irregularities. E.g., Merrill's
veiling theory is supported by Serkowski's (1966a, b) recent discovery
of large amounts of plane polarization in some Mira stars at minimum
light. This polarization can be explained by graphite flakes, condensed
in the atmosphere of these stars, presuming that they are aligned by
stellar magnetic fields (Donn et al. 1966; Wickramasinghe 1968).
Magnetic forces may play an important role in the formation of the
envelopes of Be stars. Of course, Struve's (1931) suggestion of
rotationally forced ejection in a star rotating at the rotational limit
in which its equatorial rotational velocity is first sufficient to
balance by centrifugal effects the gravitational attraction of the star
at its equator, is correct. But an additional force is required to move
the matter outward from the region just above the star's equator. The
complex kinematic behaviour of the shell, the occurrence of stars such
as Pleione, which seem able to lose and reform their shell at intervals,
is particularly suggestive of the presence of forces which trend to
drive the gases away from the star. Even quite weak magnetic fields
could produce significant dynamical effects in such a shell (Crampin and
Hoyle 1960; Limber and Marlborough 1968). Hazlehurst (1967) studied in a
recent paper the magnetic release of a circumstellar ring, and he found
that the gases describe a decelerated motion, compatible with the
observed spectral properties of circumstellar shells. From the ultimate
velocity of the material an observational determination of the magnetic
field in the stellar photosphere will be possible.*
* About problems of irregular variations in light and radial velocity of
Be, Of and WR stars I refer to the excellent book The Early Type Stars
by Anne B. Underhill (Reidel Publishing Company, 1966).
We would have a better understanding of the observed period-variations
in eclipsing binaries, if an adequate electromagnetic theory of the gaseous
streams in the systems had been elaborated. It appears from the work by
Plavec and Schneller that the most erratic O-C diagrams are obtained for
contact and undetached systems. If an O-C diagram has random walk
properties, then the underlying physical processes that give rise to
the random period fluctuations, are themselves random processes. Wood's
hypothesis of mass ejection for the explanation of the period
fluctuations, if the areas of ejection are distributed over the surface
at random, fits the criterion of randomness, but the required masses are
too high. However, we might have a very efficient agent for angular
momentum changes in the interaction of the ionized gaseous streams
moving around the components with the magnetic fields of the stars.
Magnetic fields might play an even greater role in hot short-period
eruptive binaries and in symbiotic stars. Babcock measured a magnetic field
of 1000 gauss in the symbiotic variable AG Pegasi. The configuration in
eruptive binaries, a highly ionized disk, a strongly flickering hot component
ejecting highly ionized material into the disk, might be extremely unstable,
especially if the components have strong magnetic fields. It is just possible
that the magnetic and gravitational instability of such a configuration might
lead from time to time to major eruptions. According to my opinion the seat of
the eruptions might be the plasma surrounding the stars, not a stellar
component.
According to Ambarzumjan's (1954) hypothesis, the continuous emission
observed in the spectra of the T Tauri type variables and UV Ceti type
stars during their outbursts originates from relativistic electrons in
the magnetic fields of these stars.
Random processes may influence the pulsation of the stars, giving rise
to irregular fluctuations in the light and radial velocity curve and in
the period. The triggering mechanism of the pulsation, which is sought
in the convective layers of the stars, may especially be sensitive to
magnetic activity.
Epstein (1950) has shown in an important paper that in highly centrally
concentrated stellar models the period of the fundamental mode is
determined primarily by conditions in the envelope and that the period
is almost independent of conditions in the central regions where most of
the mass is located. This result suggests that stellar pulsation, at
least in giant and supergiant-like stars, is a fairly superficial
phenomenon effecting only the outer stellar layers. The higher modes are
even more sensitive to properties of the most external layers of the
star, since these modes have higher relative amplitudes near the
surface.
Indeed, red variables, where the outer layers play a great role, have
very erratic light variation, whereas classical Cepheids and most RR
Lyrae stars show very little if any irregularities.
Zhevakin introduced the peripheral zone of He II critical ionization
as the excitation mechanism of the pulsation. He (1959) developed an
interesting theory of semiregular and irregular variables. The period of
oscillation of the inner region of the star is constant to a high degree
of accuracy. The nonadiabatic oscillations of the atmosphere show
relative to the adiabatic oscillations of the inner regions a phase
shift, whose value depends primarily on how close is the ionization zone
to the stellar surface. Random fluctuations in the position of the zone
change the phase shift, and in this way the period of the outer zones
will fluctuate about the period of oscillations of the inner region.
If the driving mechanism of the pulsation is affected by random
perturbations, wee may expect a suppression of the amplitude of the
pulsation relative to stars free from such perturbations. As it is well
known, semiregular red variables differ from the longperiod variables
only in their smaller amplitudes (Fig. 3).
The RR Lyrae-variables with the Blashko-effect have very complicated
O-C diagrams. Though the Blashko-effect is a periodic phenomenon, it
causes great random fluctuations both in the fundamental and in the
secondary period (Fig. 4). As a period-amplitude diagram for RRab-stars
in M3, taken from a paper by Szeidl (1965), shows (Fig. 5), the mean
amplitudes of the RRab stars with Blashko-effect are much smaller than
the amplitudes of RRab stars with stable light curves.
Babcock discovered a strongly variable, magnetic field in RR Lyrae
which ranges from +1200 to -1600 gauss. Julia Balázs (1959) has shown
that there was some correlation between Babcock's measures and the
Blashko-effect of this star: the maximum positive and maximum negative
fields were associated with the maximum and minimum light amplitudes,
respectively.
 Fig. 3. Period-amplitude relation for longperiod (points) and semiregular
(crosses) variables in Sagittarius.
Fig. 3. Period-amplitude relation for longperiod (points) and semiregular
(crosses) variables in Sagittarius.
 Fig. 4. O-C diagrams for the fundamental and secondary periods of RR Lyrae.
She made the proposal that RR Lyrae is an oblique rotator with a
rotation period of 41 days, which is the period of the Blashko-effect.
Preston (1967) has observed RR Lyrae for the Zeeman effect in 1963 and
1964 some 50 times and has not once found a measurable field. Yet, this
negative result does not disprove, that the Blashko-effect and the
irregularities connected with it are of magnetic origin. As Fig. 6
prepared by Szeidl shows, the Blashko-effect is a very erratic
phenomenon, the amplitude of the phase variations and that of the
maximum light variations are changing strongly from time to time, they
are sometimes scarcely observable.* The same may happen with the
magnetic field. In any case, the greatest part of magnetic activity
might take place, as on the sun, below the photosphere.
* In RR Gem a strong Blashko-effect was observed till about 1937 which
disappeared later.
For Delta Scuti variables and dwarf Cepheids we do not observe the
suppression of the amplitude in stars with secondary periodicities,
and such stars have the same simple O-C diagrams as variables with
stable light curves. Here, the secondary periods may originate from non
random influences, e.g. from tidal effects as proposed by Fitch (1962).
Fig. 4. O-C diagrams for the fundamental and secondary periods of RR Lyrae.
She made the proposal that RR Lyrae is an oblique rotator with a
rotation period of 41 days, which is the period of the Blashko-effect.
Preston (1967) has observed RR Lyrae for the Zeeman effect in 1963 and
1964 some 50 times and has not once found a measurable field. Yet, this
negative result does not disprove, that the Blashko-effect and the
irregularities connected with it are of magnetic origin. As Fig. 6
prepared by Szeidl shows, the Blashko-effect is a very erratic
phenomenon, the amplitude of the phase variations and that of the
maximum light variations are changing strongly from time to time, they
are sometimes scarcely observable.* The same may happen with the
magnetic field. In any case, the greatest part of magnetic activity
might take place, as on the sun, below the photosphere.
* In RR Gem a strong Blashko-effect was observed till about 1937 which
disappeared later.
For Delta Scuti variables and dwarf Cepheids we do not observe the
suppression of the amplitude in stars with secondary periodicities,
and such stars have the same simple O-C diagrams as variables with
stable light curves. Here, the secondary periods may originate from non
random influences, e.g. from tidal effects as proposed by Fitch (1962).
 Fig. 5. Period-amplitude diagram for RRab stars in M3 according to Szeidl (1965)
The dotted line shows the relation valid for stable light curves, the vertical
lines show the limits of A_pg for RRab stars with Blashko-effect.
RU Camelopardalis, a peculiar W Virginis-type Cepheid offers now a
unique opportunity for studying the interplay between pulsation and
irregular stellar activity. Demers and Fernie (1966) made three years
ago the remarkable discovery that the star nearly stopped its light
variation. Considering all available photoelectric observations I was
able to show (Detre 1966) that the star exhibited cyclic amplitude
variations with a mean cycle of about 5 years. Therefore, I expected an
increase in the amplitude for the year 1967. Indeed the amplitude began
to increase in the spring 1967, and in the summer it reached 0.3 mg. in
V and nearly half a magnitude in B. But immediately, after Fernie and
myself have reported about this amplitude increase at the Prague IAU
meeting, the amplitude came back very rapidly to the small value it had
in 1966 (Fig. 7). At first the light minimum, a little later the maximum
passed to its former value. The star needed in both cases only four
cycles of its 22 day-variation to restore the small amplitude.
The most important point we should know, how the spectrum changed.
Faraggiana and Hack (1967) studied 11 high dispersion spectrograms taken
by Prof. Deutsch between 1956 and 1961 when the light amplitude was
normal. They observed hydrogen emission-lines from minimum to maximum
and emission cores in the H and K lines on all the spectrograms
sufficiently exposed in this region. The radial velocity curve obtained
from these lines was shifted with respect to the curve for the
absorption lines by about -70 km/sec, suggesting that the chromosphere
of the star was in expansion. Demers and Crampton (1966) taking spectra
during the small amplitude stage, state that no emission lines are
visible. To the same conclusion comes Wallerstein (1967, 1968) using
Lick coudé spectra. But unfortunately, these spectra do not contain the H,
K lines region. I wonder if there are any spectra taken during the
quiescent or temporary recovery stage similar to those obtained formerly
by Prof. Deutsch.
According to my opinion the pulsation mechanism of the star is very sensitive
to changes of its magnetic field and we witness the effects of such changes in
the last time. I hope, the star will yet give opportunity to study this
question. At present it shows irregular light variations with a V-amplitude
smaller than 0.1 magnitude.
Fig. 5. Period-amplitude diagram for RRab stars in M3 according to Szeidl (1965)
The dotted line shows the relation valid for stable light curves, the vertical
lines show the limits of A_pg for RRab stars with Blashko-effect.
RU Camelopardalis, a peculiar W Virginis-type Cepheid offers now a
unique opportunity for studying the interplay between pulsation and
irregular stellar activity. Demers and Fernie (1966) made three years
ago the remarkable discovery that the star nearly stopped its light
variation. Considering all available photoelectric observations I was
able to show (Detre 1966) that the star exhibited cyclic amplitude
variations with a mean cycle of about 5 years. Therefore, I expected an
increase in the amplitude for the year 1967. Indeed the amplitude began
to increase in the spring 1967, and in the summer it reached 0.3 mg. in
V and nearly half a magnitude in B. But immediately, after Fernie and
myself have reported about this amplitude increase at the Prague IAU
meeting, the amplitude came back very rapidly to the small value it had
in 1966 (Fig. 7). At first the light minimum, a little later the maximum
passed to its former value. The star needed in both cases only four
cycles of its 22 day-variation to restore the small amplitude.
The most important point we should know, how the spectrum changed.
Faraggiana and Hack (1967) studied 11 high dispersion spectrograms taken
by Prof. Deutsch between 1956 and 1961 when the light amplitude was
normal. They observed hydrogen emission-lines from minimum to maximum
and emission cores in the H and K lines on all the spectrograms
sufficiently exposed in this region. The radial velocity curve obtained
from these lines was shifted with respect to the curve for the
absorption lines by about -70 km/sec, suggesting that the chromosphere
of the star was in expansion. Demers and Crampton (1966) taking spectra
during the small amplitude stage, state that no emission lines are
visible. To the same conclusion comes Wallerstein (1967, 1968) using
Lick coudé spectra. But unfortunately, these spectra do not contain the H,
K lines region. I wonder if there are any spectra taken during the
quiescent or temporary recovery stage similar to those obtained formerly
by Prof. Deutsch.
According to my opinion the pulsation mechanism of the star is very sensitive
to changes of its magnetic field and we witness the effects of such changes in
the last time. I hope, the star will yet give opportunity to study this
question. At present it shows irregular light variations with a V-amplitude
smaller than 0.1 magnitude.
 Fig. 6. Variations in the Blashko-effect of RR Lyrae.
Fig. 6. Variations in the Blashko-effect of RR Lyrae.
 Fig. 7. Light maxima and minima of RU Cam in V, according to photoelectric
observations obtained by Szeidl at the 24" reflector of the Konkoly Observatory.
I have only touched some few aspects of irregular stellar activity. Our
field is tremendous. From the theoretical side it comprises questions of
stellar stability, pulsation theory, turbulence and shock wave theory,
i.e., the dynamic theory of stellar envelopes, further, celestial
mechanics, magnetohydrodynamics and questions of stellar evolution. From
the observational side it extends over all periodic or non-periodic
variables, over intrinsic as well as eclipsing variables. Its complete
understanding postulates the knowledge of solar physics in highest
degree. And the reason for not yet proposing a symposium with solar
physicists, is because they would have a great advantage over us. We may
hope that not in the far future variable star astronomers will be able
to give the same help to solar physicists as they give at present to us.
REFERENCES
Ambarzumjan, V. A., 1954. Comm. Byurakan Obs. No. 13.
Ashbrook, J., Duncombe, R. L. and Van Woerkom, A. J. J., 1954, Astr. J. 59, 12.
Balázs-Detre, Julia and Detre, L., 1965, Kl. Veröff. Remeis-Sternw. Bamberg IV,
No. 40 p. 184.
Balázs-Detre, Julia, 1959, Kl. Veröff. Remeis-Sternw. Bamberg 27, 26.
Bonsack W. K. and Culver, R. B., 1966, Astrophys. J. 145, 767.
Christy, R. F., 1965, Kl. Veröff. Remeis-Sternw. Bamberg, 40, 77.
Crampin, J. and Hoyle, F., 1960, Mon. Not. R. astr. Soc. 120, 33.
Demers, S. and Crampton, D., 1966, Astr. J. 71, 852.
Demers, S. and Fernie, J. D., 1966, Astrophys. J. 144, 440.
Detre, L., 1966, Inf. Bul. Var. Stars No. 152. (IBVS N°.152)
Deutsch, A. J., 1956, Astrophys. J. 123, 210.
Deutsch, A. J., 1966, Stellar Evolution. Plenum Press New York p. 377.
Deutsch, A. J., 1967, IAU Circ. No. 2020.
Donn, B., Stecher, T. P., Wickramasinghe, N. C. and Williams, D. A., 1966, Astrophys.
J. 145, 949.
Durney, B. R., Faulkner, J., Gribbin, J. R. and Roxburgh, I. W., 1968, Nature 218, 20.
Epstein, J., 1950, Astrophys. J. 112, 6.
Faraggiana, R. and Hack, M., 1967, Z. Astrophys. 66, 343.
Godoli, G., 1967, Atti dell'XI. Convegno, Padova, p. 224.
Griffin, R. F., 1964, Observatory 83, 255.
Haro, G., 1967, Stars and Stellar Systems. Vol. VIII. 141.
Hazlehurst, J., 1967, Z. Astrophys. 65, 311.
Herbig, G. H., 1952, Astrophys. J. 116, 369.
Herbig, G. H., 1960, Astrophys. J. 132, 76.
Herbig, G. H., 1966, Vistas in Astr. 8, 109.
Herbig, G. H., Preston, G. W., Smak, J. and Paczynski, B., 1967, Astrophys. J. 141, 617.
Herbig, G. H., 1968. Inf. Bul. Var. Stars No. 243. (IBVS N°.243)
Jacobsen, T. S., 1960, Publ. Dom. Astrophys. Obs. Victoria 10, 145.
Jenkins, E. B. and Morton, D. C., 1967, Nature 215, 1257.
Kraft, R. P., 1957, Astrophys. J. 125, 336.
Kraft, R. P., Preston, G. W. and Wolff, S. C., 1964, Astrophys. J. 140, 235.
Kraft, R. P., 1967, IAU Symp. 28, p. 236.
Kron, G. E., 1947, Publ. astr. Soc. Pacific 59, 261.
Kron, G. E., 1952, Astrophys. J. 115, 301.
Kuhi, L. V., 1964, Astrophys. J. 140, 1408.
Kuhi, L. V., 1966, Stellar Evolution. Plenum Press New York, p. 373.
Kurochkin, N. E., 1962, Perem. Zvezdy 14, 284.
Kwee, K. K., 1967, Bull. astr. Inst. Netherl. Suppl. 2, 97.
Leighton, R. B., 1964, Astrophys. J. 140, 1120.
Liller, W., 1968, Astrophys. J. 151, 589.
Limber, D. N. and Marlborough, J. M., 1968, Astrophys. J. 152, 181.
Loreta, E., 1934, Astr. Nachr. 254, 151.
Lortet-Zuckermann, M. C., 1966, Ann. Astrophys. 29, 205.
Lovell, B., 1964, Observatory 84, 191.
Lukatskaya, F. I., 1966, Per. Zvezdy 16, 168.
Lukatskaya, F. I., 1968, Inf. Bul. Var. Stars No. 295. (IBVS N°.295)
Merrill, P. W., 1960, Stellar Atmospheres. The University of Chicago Press, p. 512.
O'Keefe, J. A., 1939, Astrophys. J. 90, 294.
Paczynski, B. and Ziólkowski, J., 1968, Acta Astr. 18, 255.
Penston, M. V., 1968, Inf. Bul. Var. Stars 255. (IBVS N°.255)
Preston, G. W., 1967, The Magnetic and Related Stars. Mono Book Corp. Baltimore, p. 3.
Schmitt, J. L., 1968, Nature 218, 663.
Serkowski, K., 1966a, Astrophys. J. 144, 857.
Serkowski, K., 1966b, Inf. Bul. Var. Stars No. 141. (IBVS N°.141)
Slee, O. B., Komesaroff, M. M. and McCullock, P. M., 1968, Nature 219, 342.
Sharpless, S., Riegel, K. and Williams, J. O., 1966, R. astr. Soc. Can. 60, 15.
Sterne, T. E., 1934, Harvard Bul. 896, 16 and 17.
Struve, O., 1931, Astrophys. J. 73, 94.
Szeidl, B., 1965, Mitt. Sternwarte Budapest No. 58 (CoKon N°.58)
Tsessevich, V. P. and Dragomirezkaya, B. A., 1967, Sky Tel. 34, 366.
Underhill, A. B., 1960, IAU Symp. No. 12, p. 88.
Vaughan, A. H. Jr., and Zirin, H., 1968, Astrophys. J. 152, 123.
Wallerstein, G. and Crampton, D., 1967, Astrophys. J. 149, 225.
Wallerstein, G., 1968(a), Astrophys. J. 151, 1011.
Wallerstein, G., 1968(b), Observatory 88, 111.
Weyman, R., 1962, Astrophys. J. 136, 476 and 844.
Wickramasinghe, N. C., 1968, Mon. Not. R. astr. Soc. 140, 273.
Wilson, O. C. and Bappu, M. K. Vainu, 1957, Astrophys. J. 125, 661.
Zhevakin, S. A., 1959, Astr. Zu. 36, 394.
Fig. 7. Light maxima and minima of RU Cam in V, according to photoelectric
observations obtained by Szeidl at the 24" reflector of the Konkoly Observatory.
I have only touched some few aspects of irregular stellar activity. Our
field is tremendous. From the theoretical side it comprises questions of
stellar stability, pulsation theory, turbulence and shock wave theory,
i.e., the dynamic theory of stellar envelopes, further, celestial
mechanics, magnetohydrodynamics and questions of stellar evolution. From
the observational side it extends over all periodic or non-periodic
variables, over intrinsic as well as eclipsing variables. Its complete
understanding postulates the knowledge of solar physics in highest
degree. And the reason for not yet proposing a symposium with solar
physicists, is because they would have a great advantage over us. We may
hope that not in the far future variable star astronomers will be able
to give the same help to solar physicists as they give at present to us.
REFERENCES
Ambarzumjan, V. A., 1954. Comm. Byurakan Obs. No. 13.
Ashbrook, J., Duncombe, R. L. and Van Woerkom, A. J. J., 1954, Astr. J. 59, 12.
Balázs-Detre, Julia and Detre, L., 1965, Kl. Veröff. Remeis-Sternw. Bamberg IV,
No. 40 p. 184.
Balázs-Detre, Julia, 1959, Kl. Veröff. Remeis-Sternw. Bamberg 27, 26.
Bonsack W. K. and Culver, R. B., 1966, Astrophys. J. 145, 767.
Christy, R. F., 1965, Kl. Veröff. Remeis-Sternw. Bamberg, 40, 77.
Crampin, J. and Hoyle, F., 1960, Mon. Not. R. astr. Soc. 120, 33.
Demers, S. and Crampton, D., 1966, Astr. J. 71, 852.
Demers, S. and Fernie, J. D., 1966, Astrophys. J. 144, 440.
Detre, L., 1966, Inf. Bul. Var. Stars No. 152. (IBVS N°.152)
Deutsch, A. J., 1956, Astrophys. J. 123, 210.
Deutsch, A. J., 1966, Stellar Evolution. Plenum Press New York p. 377.
Deutsch, A. J., 1967, IAU Circ. No. 2020.
Donn, B., Stecher, T. P., Wickramasinghe, N. C. and Williams, D. A., 1966, Astrophys.
J. 145, 949.
Durney, B. R., Faulkner, J., Gribbin, J. R. and Roxburgh, I. W., 1968, Nature 218, 20.
Epstein, J., 1950, Astrophys. J. 112, 6.
Faraggiana, R. and Hack, M., 1967, Z. Astrophys. 66, 343.
Godoli, G., 1967, Atti dell'XI. Convegno, Padova, p. 224.
Griffin, R. F., 1964, Observatory 83, 255.
Haro, G., 1967, Stars and Stellar Systems. Vol. VIII. 141.
Hazlehurst, J., 1967, Z. Astrophys. 65, 311.
Herbig, G. H., 1952, Astrophys. J. 116, 369.
Herbig, G. H., 1960, Astrophys. J. 132, 76.
Herbig, G. H., 1966, Vistas in Astr. 8, 109.
Herbig, G. H., Preston, G. W., Smak, J. and Paczynski, B., 1967, Astrophys. J. 141, 617.
Herbig, G. H., 1968. Inf. Bul. Var. Stars No. 243. (IBVS N°.243)
Jacobsen, T. S., 1960, Publ. Dom. Astrophys. Obs. Victoria 10, 145.
Jenkins, E. B. and Morton, D. C., 1967, Nature 215, 1257.
Kraft, R. P., 1957, Astrophys. J. 125, 336.
Kraft, R. P., Preston, G. W. and Wolff, S. C., 1964, Astrophys. J. 140, 235.
Kraft, R. P., 1967, IAU Symp. 28, p. 236.
Kron, G. E., 1947, Publ. astr. Soc. Pacific 59, 261.
Kron, G. E., 1952, Astrophys. J. 115, 301.
Kuhi, L. V., 1964, Astrophys. J. 140, 1408.
Kuhi, L. V., 1966, Stellar Evolution. Plenum Press New York, p. 373.
Kurochkin, N. E., 1962, Perem. Zvezdy 14, 284.
Kwee, K. K., 1967, Bull. astr. Inst. Netherl. Suppl. 2, 97.
Leighton, R. B., 1964, Astrophys. J. 140, 1120.
Liller, W., 1968, Astrophys. J. 151, 589.
Limber, D. N. and Marlborough, J. M., 1968, Astrophys. J. 152, 181.
Loreta, E., 1934, Astr. Nachr. 254, 151.
Lortet-Zuckermann, M. C., 1966, Ann. Astrophys. 29, 205.
Lovell, B., 1964, Observatory 84, 191.
Lukatskaya, F. I., 1966, Per. Zvezdy 16, 168.
Lukatskaya, F. I., 1968, Inf. Bul. Var. Stars No. 295. (IBVS N°.295)
Merrill, P. W., 1960, Stellar Atmospheres. The University of Chicago Press, p. 512.
O'Keefe, J. A., 1939, Astrophys. J. 90, 294.
Paczynski, B. and Ziólkowski, J., 1968, Acta Astr. 18, 255.
Penston, M. V., 1968, Inf. Bul. Var. Stars 255. (IBVS N°.255)
Preston, G. W., 1967, The Magnetic and Related Stars. Mono Book Corp. Baltimore, p. 3.
Schmitt, J. L., 1968, Nature 218, 663.
Serkowski, K., 1966a, Astrophys. J. 144, 857.
Serkowski, K., 1966b, Inf. Bul. Var. Stars No. 141. (IBVS N°.141)
Slee, O. B., Komesaroff, M. M. and McCullock, P. M., 1968, Nature 219, 342.
Sharpless, S., Riegel, K. and Williams, J. O., 1966, R. astr. Soc. Can. 60, 15.
Sterne, T. E., 1934, Harvard Bul. 896, 16 and 17.
Struve, O., 1931, Astrophys. J. 73, 94.
Szeidl, B., 1965, Mitt. Sternwarte Budapest No. 58 (CoKon N°.58)
Tsessevich, V. P. and Dragomirezkaya, B. A., 1967, Sky Tel. 34, 366.
Underhill, A. B., 1960, IAU Symp. No. 12, p. 88.
Vaughan, A. H. Jr., and Zirin, H., 1968, Astrophys. J. 152, 123.
Wallerstein, G. and Crampton, D., 1967, Astrophys. J. 149, 225.
Wallerstein, G., 1968(a), Astrophys. J. 151, 1011.
Wallerstein, G., 1968(b), Observatory 88, 111.
Weyman, R., 1962, Astrophys. J. 136, 476 and 844.
Wickramasinghe, N. C., 1968, Mon. Not. R. astr. Soc. 140, 273.
Wilson, O. C. and Bappu, M. K. Vainu, 1957, Astrophys. J. 125, 661.
Zhevakin, S. A., 1959, Astr. Zu. 36, 394.