Non-Periodic Phenomena in Variable Stars
IAU Colloquium, Budapest, 1968
ON THE PRESUMED PRESUPERNOVA STAGE FOR TYPE II SUPERNOVAE
G. BARBARO, N. DALLAPORTA, C. SUMMA
Istituto di Fisica dell'Universita, Padova
(presented by Prof. L. Rosino)
ABSTRACT
The physical conditions of stars in presupernova type II stage when
the outburst is expected to be due to the Fe-He transition occurring in
its core are reviewed. The arguments showing that the star must preserve
a large envelope in this stage and therefore appear as a red supergiant
are stressed, and a lower mass limit of about 10~14 Msun for stars
undergoing the outburst is confirmed on the basis of the more recent
evaluations. Finally, the possibility that the presupernova type II
stage could be represented by the small amplitude irregular and
semiregular red variables with large masses belonging to young
population I is briefly indicated.
This paper aims partly to summarize the present situation concerning the
usually accepted interpretation of type II supernovae; and partly to
focus the main phenomenological aspects which could allow to test some
consequences of this theory. The opportunity for such a clarification is
required by the fact that not unfrequently theoretical investigations on
this subject neglect to connect the happenings in the core of the star
to its more external characteristics, so that some supplementary
considerations are necessary to bridge the gap between the two aspects
of the problem.
According to present data (Minkowski, 1964), type II supernovae occur
only in arms of spiral galaxies, and are therefore typical for early
population I. The process giving rise to the outburst must affect only
stars of relatively conspicuous mass, owing to the large values
generally quoted for the amount of matter ejected (several solar
masses); moreover, the abundance of hydrogen in the spectrum during the
explosion seems to indicate that the ejected matter is largely formed by
the envelope of the star.
Hoyle and Fowler (1960) have proposed the following mechanism as
triggering the outburst: after having evolved through the whole series
of thermonuclear reactions building heavier and heavier elements in its
inner part, the star reaches the formation of an iron core for a central
temperature of the order of a few 10^9 K; as no heavier nuclei may be
built with energy gain, for further contraction of the core, at
temperatures of the order of 8 * 10^9 K iron is transformed
endothermically into helium plus neutrons; and in order to provide the
energy necessary for such a transformation, the central part of the star
collapses in practically free fall, giving thus rise to the outburst
observed as a supernova explosion. Fowler and Hoyle have applied these
ideas to a model of a 30 Msun star with a core of 20 Msun; its evolution in
the central density rho_c - central temperature T_c plane and its crossing
the Fe-He transformation line are schematically indicated in Fig. 1.
It has been argued by Chiu (1961) and others that several neutrino
production processes, according to the current-current interaction theory
with universal constant for weak interactions could occur for temperatures
of the order of 10^9 K with such intensity as to compel the whole
structure of the star to collapse, owing to the enormous amounts of
energy subtracted by neutrinos in its center; so the question arose
whether this neutrino collapse should prevent the Fe-He collapse.
Although no definite word has been said on this subject, it is generally
considered that the usual first order calculations done to evaluate the
neutrino losses are inaccurate enough as not to allow to draw such a
conclusion, and it is implicitly supposed, on the whole, that neutrinos
contribute to accelerate the evolutionary process but do not prevent the
star to reach the Fe-He conversion line; this point of view has been
assumed in what follows.
In order to test the Fowler-Hoyle scheme on a more realistic model than
the one used by them, Barbon and al. (1965) have tried to identify the
presupernova stage with the red supergiant phase of large mass stars,
and, have considered the core to which the Fowler-Hoyle considerations
apply as being only the 15% of the total mass of the star. Further, by
studying the evolutionary sequence of the central core according to
polytropic models and with different mass values allowing for the degeneracy
of the gas, it was found that for cores with mass lower than a limiting value
M_l, degeneracy would stop the increase of temperature in order to forbid for
such stars the reaching of the Fe-He transition line, as may be seen in Fig. 1.
It turned thus out that only for masses higher than M_l the type II supernova
outburst was possible. The M_l value for the core is practically
the Chandrasekhar limit for white dwarfs ~ 1.4 Msun; so that, keeping in mind
the assumed proportion in mass between core and envelope, it resulted that
only stars with total mass higher than about ~ 10 Msun were expected to
undergo an Fe-He supernova outburst.
In a more recent and detailed research, Rakavy and Shaviv (1966) have
quite independently redetermined the evolutionary tracks of degenerate
polytropes, obtaining exactly the same results as Barbon et al. However,
they have considered in their work some other possible causes of collapse,
among others, a dynamical instability interesting for the actual problem,
occurring for very massive stars and due to the e^+ - e^- annihilation
process, whose domain is shown also in Fig. 1. It thus further appears that
polytropic models with mass higher than 30 Msun may be prevented to reach
the Fe-He line because encountering the e^+ - e^- instability domain in an
earlier stage of their evolution.
In a second paper, Rakavy and Shaviv (1967) have reconsidered the
problem according to a more accurate point of view; they integrate the
equilibrium equations for the core and determine the evolution of its
material by calculating in detail a number of reactions, allowing them
to follow the transformation from carbon to iron. The results of their
investigation show that, although the trajectories in the rho_c - T_c
plane for any of the model stars considered are much more complicated than
those obtained with the simplified polytropic models, still they do not
discard too much from them, the polytropic evolutionary curve acting as
a kind of average behaviour in respect to the more exact one, and being
thus confirmed as qualitatively reliable enough. Rakavy and Shaviv,
however, do not consider at all the envelope of the star in their
investigation; this may lead to wrong predictions when using their
results for deducing the mass range of stars able to become type II
supernovae.
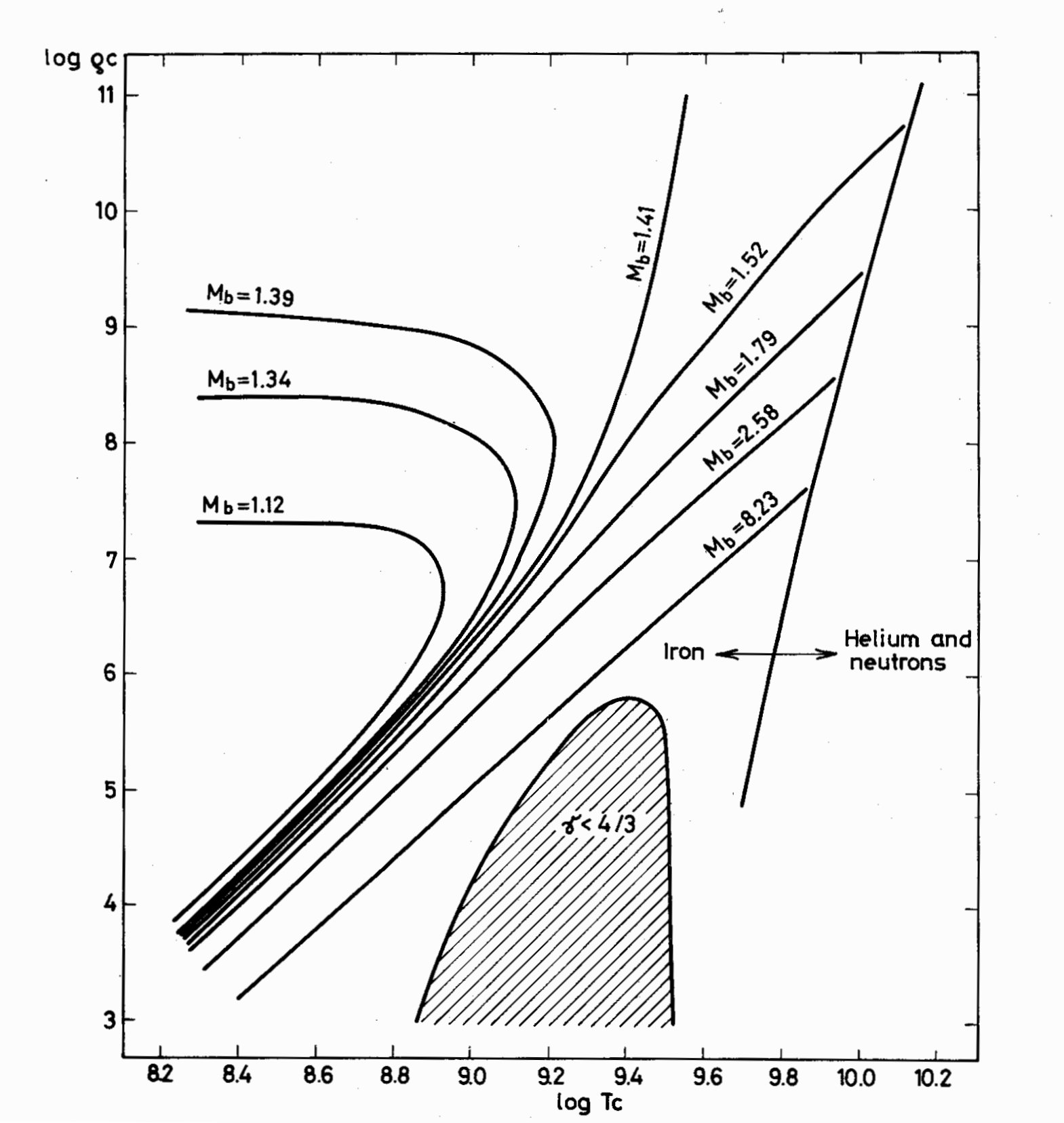 Fig. 1. Evolutionary tracks for the core. M_b represents the mass of the
core; only for M_b > 1.41 the track crosses the Fe-He transition line.
Dashed region corresponds to the region of dynamical instability due to
the e^+ - e^- annihilation process.
An adequate investigation of the problem would require the detailed
treatment of core models of Rakavy-Shaviv's type with an hydrogen
envelope. In prevision of such a work, we try here to stress some points
showing, on very general arguments, the likelihood that the hydrogen
envelope persists throughout the whole presupernova stage and therefore
cannot be ignored for comparison with data. Finally, we discuss some possible
red supergiant types which could be suspected of being presupernova stages.
Concerning the first point, we first rely on the evolved models for large
mass stars (i.e. the 15.6 Msun star of Hayashi and Cameron (1962)) followed
from the main sequence to the initial phase of carbon burning. At this stage, the
star is left with a carbonoxygen core including the 18% of the total
mass. Assuming, as usual, that no conspicuous mass loss should alter the
evolution, one may try to calculate the maximum possible amount of
nuclear fuel which should be burnt in the interior of the star in the
remaining time of its supergiant evolution up to the last presupernova
stage; this should give us the maximum amount of hydrogen transformed
into heavier elements, and therefore allow to calculate the minimum
envelope which the star preserves just before its outburst.
The luminosity L_n due to nuclear shell burnings, is expressed by:
Fig. 1. Evolutionary tracks for the core. M_b represents the mass of the
core; only for M_b > 1.41 the track crosses the Fe-He transition line.
Dashed region corresponds to the region of dynamical instability due to
the e^+ - e^- annihilation process.
An adequate investigation of the problem would require the detailed
treatment of core models of Rakavy-Shaviv's type with an hydrogen
envelope. In prevision of such a work, we try here to stress some points
showing, on very general arguments, the likelihood that the hydrogen
envelope persists throughout the whole presupernova stage and therefore
cannot be ignored for comparison with data. Finally, we discuss some possible
red supergiant types which could be suspected of being presupernova stages.
Concerning the first point, we first rely on the evolved models for large
mass stars (i.e. the 15.6 Msun star of Hayashi and Cameron (1962)) followed
from the main sequence to the initial phase of carbon burning. At this stage, the
star is left with a carbonoxygen core including the 18% of the total
mass. Assuming, as usual, that no conspicuous mass loss should alter the
evolution, one may try to calculate the maximum possible amount of
nuclear fuel which should be burnt in the interior of the star in the
remaining time of its supergiant evolution up to the last presupernova
stage; this should give us the maximum amount of hydrogen transformed
into heavier elements, and therefore allow to calculate the minimum
envelope which the star preserves just before its outburst.
The luminosity L_n due to nuclear shell burnings, is expressed by:
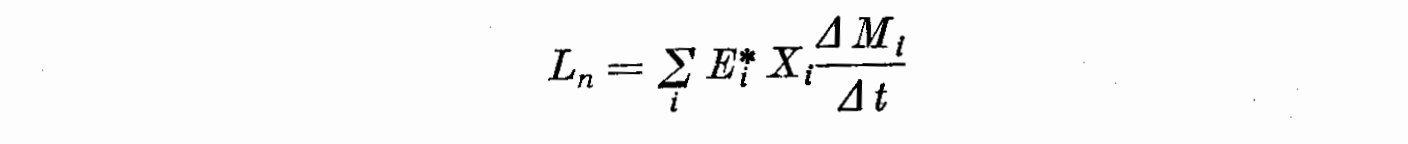 where E_i^* is the energy yield per gram of the i-th given fuel, X_i its
concentration in the i-th burning shell, Delta M_i / Delta t the
variation of mass of the i-th shell per unit time. The maximum value for
each of the Delta M_i may be immediately obtained by supposing its
corresponding shell as the only one burning, thus
where E_i^* is the energy yield per gram of the i-th given fuel, X_i its
concentration in the i-th burning shell, Delta M_i / Delta t the
variation of mass of the i-th shell per unit time. The maximum value for
each of the Delta M_i may be immediately obtained by supposing its
corresponding shell as the only one burning, thus
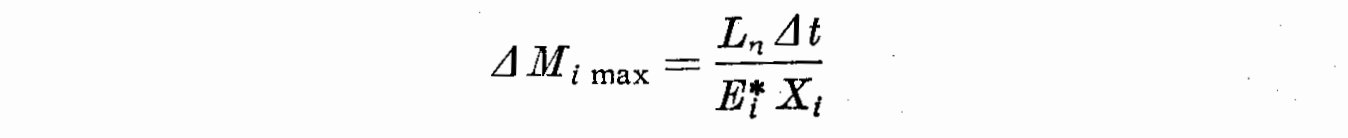 A more conservative assumption is reached by assuming an evolution in
which the different shells advance in a parallel way, the amounts of
different fuels burnt in each shell being approximately equal. That is,
we assume:
A more conservative assumption is reached by assuming an evolution in
which the different shells advance in a parallel way, the amounts of
different fuels burnt in each shell being approximately equal. That is,
we assume:
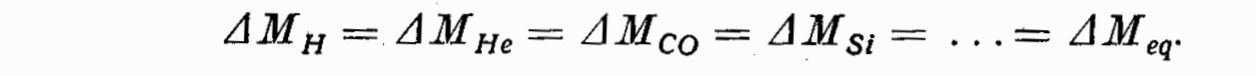 If we disregard the possible luminosity loss due to expansion of the
outer envelope which in no case (except flashes, not to be expected for
non degenerate matter) should be very large, and assuming that eventual
neutrino losses, however big, should be provided for by the central
burning of the core, the nuclear shell burnings luminosity L_n could be
substituted with the total observed luminosity L in order to arrive at
maximum estimations; thus we get:
If we disregard the possible luminosity loss due to expansion of the
outer envelope which in no case (except flashes, not to be expected for
non degenerate matter) should be very large, and assuming that eventual
neutrino losses, however big, should be provided for by the central
burning of the core, the nuclear shell burnings luminosity L_n could be
substituted with the total observed luminosity L in order to arrive at
maximum estimations; thus we get:
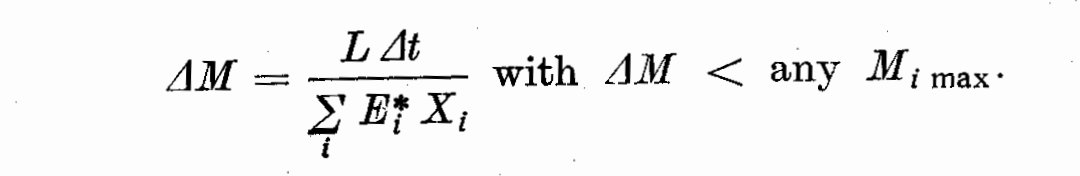 Assuming the data of the Hayashi model
Assuming the data of the Hayashi model
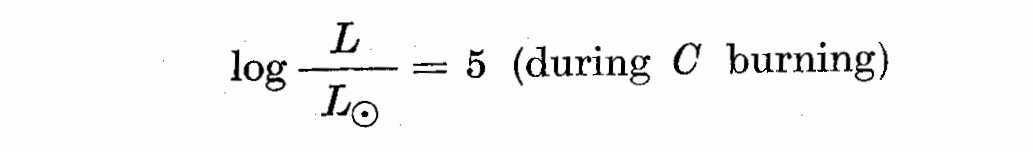 Delta t = 8 * 10^5 years from C burning to the explosion
and the constants tabulated in Table I, we obtain for the Delta M's the
results given also in Table I. These are probably rather insensitive to
errors of L and Delta t. Should in fact the luminosity increase due i.e. to
neutrino emission, then the evolution time Delta t should correspondingly
decrease, so that the product L Delta t would not change much.
If we define the core of the star as the central portion of it for which
mu = const ~ 2, that is the whole portion inside the He burning shell, then
according to data of Table I, the medium increase of it is Delta M / M = 0.06,
with extreme possibilities ranging from no increase at all
(should the He burning shell stop burning) and maximum increase of about 0.23
(should the He burn alone). The core fraction therefore should increase from
the 0.18 value in the last Hayashi model to 0.24+0.17-0.06
Table I
Delta t = 8 * 10^5 years from C burning to the explosion
and the constants tabulated in Table I, we obtain for the Delta M's the
results given also in Table I. These are probably rather insensitive to
errors of L and Delta t. Should in fact the luminosity increase due i.e. to
neutrino emission, then the evolution time Delta t should correspondingly
decrease, so that the product L Delta t would not change much.
If we define the core of the star as the central portion of it for which
mu = const ~ 2, that is the whole portion inside the He burning shell, then
according to data of Table I, the medium increase of it is Delta M / M = 0.06,
with extreme possibilities ranging from no increase at all
(should the He burning shell stop burning) and maximum increase of about 0.23
(should the He burn alone). The core fraction therefore should increase from
the 0.18 value in the last Hayashi model to 0.24+0.17-0.06
Table I
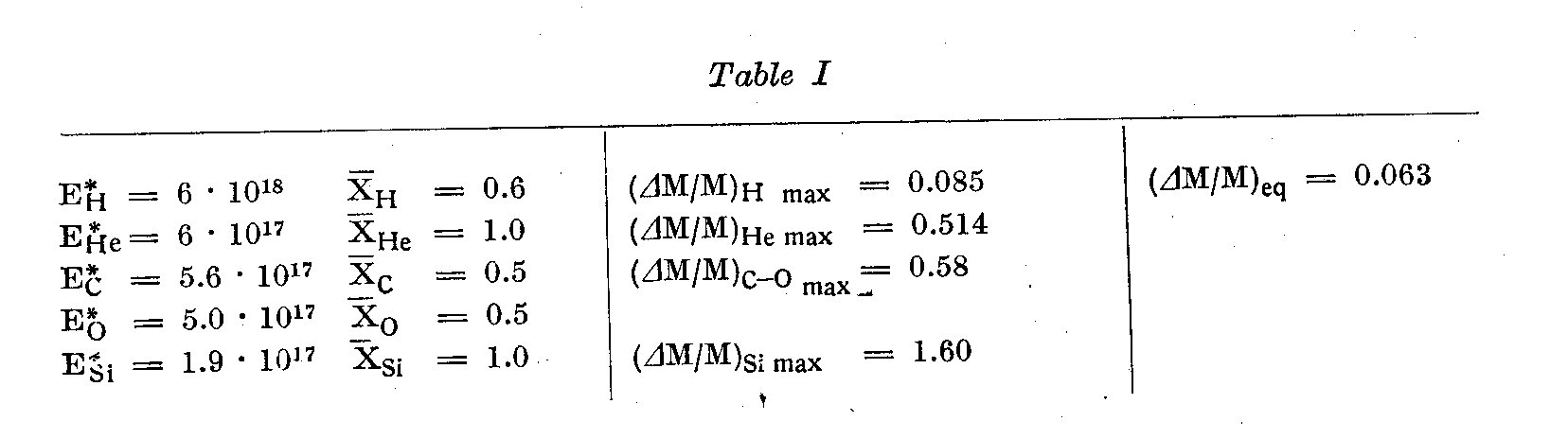 Should we instead consider the core as being only the innermost part
inside the deeper burning shell (at the end of the iron core), then only
a fraction of the previous increase is expected, which almost justifies
the assumption of a constant core made by Barbon et al.
If now, according to Rakavy and Shaviv, we consider that only cores with mass
greater than 2 Msun can surely evolve towards the Fe-He transition line (the
case of masses between 1.4 Msun and 2 Msun has not yet adequately studied by
these authors), then we obtain for the lower limit of the total mass of the
presupernova the value M_l ~- 8.3 Msun+2.7-3.3 with the first definition of
the core, and the value M_l ~ 11 Msun with the second one. Moreover, if we
accept Weymann's data (1961) on mass loss of red supergiants (20 per cent of
the total mass for alpha Ori), we obtain for the lower limits of the initial
masses of future type II supernovae the values M_l = 10.5+3.5-4.3 Msun
for the first type core definition, and M ~ 14 Msun for the other. Therefore,
the results of Barbon et al., on the mass range of type II supernovae, are
practically confirmed by the present analysis.
The absolute visual magnitude of a main sequence star with mass around
10-14 Msun lies in the range -3 to -4. According to Limber's (1960)
original luminosity function for the sun's neighbourhood, this gives us
for the number of stars per cubic parsec with luminosity higher than
this limit, the value ~1.10^-4. Assuming a mean lifetime for these stars
on the main sequence of T = 1.5 * 10^7 years, and equilibrium between
birth rate and death rate functions, we obtain some 0.7 * 10^-11 type II
supernovae per cubic parsec per year. Considering such events to occur
possibly in all the outer disc portion of the Galaxy, we arrive at a
frequency of a few events per year. Compared with data, this value is
too high by a factor of about 100. Considering, however, the enormous
uncertainty of the present evaluation, especially concerning the volume
of the galaxy occupied by population I, and the extrapolation of
the luminosity function for the sun's neighbourhood to the whole volume,
one cannot conclude that the present disagreement is sufficient to disprove
the theory. Moreover, it must be stressed that the present evaluation,
although too large greatly improves the figure obtained by lowering the
mass limit M, for supernovae to about 2 Msun as frequently done. Probably,
should the Fe-He conversion mechanism be true for triggering supernovae,
there should still be some other reason to further increase the lower
mass limit for their occurrence.
As a further remark, according to Rakavy and Shaviv, cores with mass
higher than ~ 30 Msun fail to reach the Fe--He transition line, as they
are stopped earlier in their evolutionary path by the e^+ - e^- pair
creation zone, in which the star grows unstable. The fate of such huge
stars has been investigated by Fraley (1968) and found to lead them to a
kind of softer collapse, which should perhaps show in a slower increase
of the light output at the beginning of the explosion. Such a situation
has been observed in some anomalous supernovae such as SN 96 in NGC 1058
discussed by Zwicky (1964) and Bertola (1963), which, moreover,
appears also at minimum to be an exceptionally luminous star (M_v ~= -9);
another example of the same type of event might have been eta Car. The
e^+ - e^- collapse might perhaps be taken into consideration for interpreting
such kind of events.
Concerning the second question of trying to identify the red supergiant
types which could be considered as last presupernova stages, we have
focused our attention on the red irregular and semiregular variables.
Although the difficulties of determining their low temperatures makes it
difficult to locate them exactly in the H-R diagram, still there may be
some suspicion that light variability occurs generally for the coolest
and reddest among giants, and this could connect its cause to the fact
of being near the Hayashi limit. If this were the case, and if the
evolutionary trend in the presupernova phase was still from left to
right in the H-R plane, then the connection of red variability with such
a phase could appear not too unlikely.
Not many reliable data on red variables of small amplitude are at hand.
In order to partially supply for this lack of knowledge, we have collected the
stars of this kind belonging to galactic clusters whose location in the H-R
plane is determined. The data concerning them are given in Table II and their
position in the H-R plane shown in Fig. 2; some Mira type stars belonging to
the clusters are included for comparison.
At first sight, the red variables appear to be divided into two groups:
an upper one of supergiants evolving from large mass clusters of early
population I; and a lower one of giants belonging to low mass clusters
of disk population. Mira variables are found only in this second group,
so that small amplitude red variables of this group could be considered
as transition stages leading to the Mira situation.
One would like to investigate whether the two groups outlined are in fact
physically different, and separated by a real gap between them. Some indication
on this question may be obtained from Table III, in which the clusters have
been divided into three groups according to their different ages, and which
contains the following data: number of clusters, number of red giants, number
of red variables, ratio of the number of variables to the total number of
giants for each group. The values into brackets for the third group include
stars which have not been studied yet and which, therefore, are only suspected
variables. It is seen that for the first or large mass group, the ratio of
column 4 is much higher than for the third or low mass group.
Should we instead consider the core as being only the innermost part
inside the deeper burning shell (at the end of the iron core), then only
a fraction of the previous increase is expected, which almost justifies
the assumption of a constant core made by Barbon et al.
If now, according to Rakavy and Shaviv, we consider that only cores with mass
greater than 2 Msun can surely evolve towards the Fe-He transition line (the
case of masses between 1.4 Msun and 2 Msun has not yet adequately studied by
these authors), then we obtain for the lower limit of the total mass of the
presupernova the value M_l ~- 8.3 Msun+2.7-3.3 with the first definition of
the core, and the value M_l ~ 11 Msun with the second one. Moreover, if we
accept Weymann's data (1961) on mass loss of red supergiants (20 per cent of
the total mass for alpha Ori), we obtain for the lower limits of the initial
masses of future type II supernovae the values M_l = 10.5+3.5-4.3 Msun
for the first type core definition, and M ~ 14 Msun for the other. Therefore,
the results of Barbon et al., on the mass range of type II supernovae, are
practically confirmed by the present analysis.
The absolute visual magnitude of a main sequence star with mass around
10-14 Msun lies in the range -3 to -4. According to Limber's (1960)
original luminosity function for the sun's neighbourhood, this gives us
for the number of stars per cubic parsec with luminosity higher than
this limit, the value ~1.10^-4. Assuming a mean lifetime for these stars
on the main sequence of T = 1.5 * 10^7 years, and equilibrium between
birth rate and death rate functions, we obtain some 0.7 * 10^-11 type II
supernovae per cubic parsec per year. Considering such events to occur
possibly in all the outer disc portion of the Galaxy, we arrive at a
frequency of a few events per year. Compared with data, this value is
too high by a factor of about 100. Considering, however, the enormous
uncertainty of the present evaluation, especially concerning the volume
of the galaxy occupied by population I, and the extrapolation of
the luminosity function for the sun's neighbourhood to the whole volume,
one cannot conclude that the present disagreement is sufficient to disprove
the theory. Moreover, it must be stressed that the present evaluation,
although too large greatly improves the figure obtained by lowering the
mass limit M, for supernovae to about 2 Msun as frequently done. Probably,
should the Fe-He conversion mechanism be true for triggering supernovae,
there should still be some other reason to further increase the lower
mass limit for their occurrence.
As a further remark, according to Rakavy and Shaviv, cores with mass
higher than ~ 30 Msun fail to reach the Fe--He transition line, as they
are stopped earlier in their evolutionary path by the e^+ - e^- pair
creation zone, in which the star grows unstable. The fate of such huge
stars has been investigated by Fraley (1968) and found to lead them to a
kind of softer collapse, which should perhaps show in a slower increase
of the light output at the beginning of the explosion. Such a situation
has been observed in some anomalous supernovae such as SN 96 in NGC 1058
discussed by Zwicky (1964) and Bertola (1963), which, moreover,
appears also at minimum to be an exceptionally luminous star (M_v ~= -9);
another example of the same type of event might have been eta Car. The
e^+ - e^- collapse might perhaps be taken into consideration for interpreting
such kind of events.
Concerning the second question of trying to identify the red supergiant
types which could be considered as last presupernova stages, we have
focused our attention on the red irregular and semiregular variables.
Although the difficulties of determining their low temperatures makes it
difficult to locate them exactly in the H-R diagram, still there may be
some suspicion that light variability occurs generally for the coolest
and reddest among giants, and this could connect its cause to the fact
of being near the Hayashi limit. If this were the case, and if the
evolutionary trend in the presupernova phase was still from left to
right in the H-R plane, then the connection of red variability with such
a phase could appear not too unlikely.
Not many reliable data on red variables of small amplitude are at hand.
In order to partially supply for this lack of knowledge, we have collected the
stars of this kind belonging to galactic clusters whose location in the H-R
plane is determined. The data concerning them are given in Table II and their
position in the H-R plane shown in Fig. 2; some Mira type stars belonging to
the clusters are included for comparison.
At first sight, the red variables appear to be divided into two groups:
an upper one of supergiants evolving from large mass clusters of early
population I; and a lower one of giants belonging to low mass clusters
of disk population. Mira variables are found only in this second group,
so that small amplitude red variables of this group could be considered
as transition stages leading to the Mira situation.
One would like to investigate whether the two groups outlined are in fact
physically different, and separated by a real gap between them. Some indication
on this question may be obtained from Table III, in which the clusters have
been divided into three groups according to their different ages, and which
contains the following data: number of clusters, number of red giants, number
of red variables, ratio of the number of variables to the total number of
giants for each group. The values into brackets for the third group include
stars which have not been studied yet and which, therefore, are only suspected
variables. It is seen that for the first or large mass group, the ratio of
column 4 is much higher than for the third or low mass group.
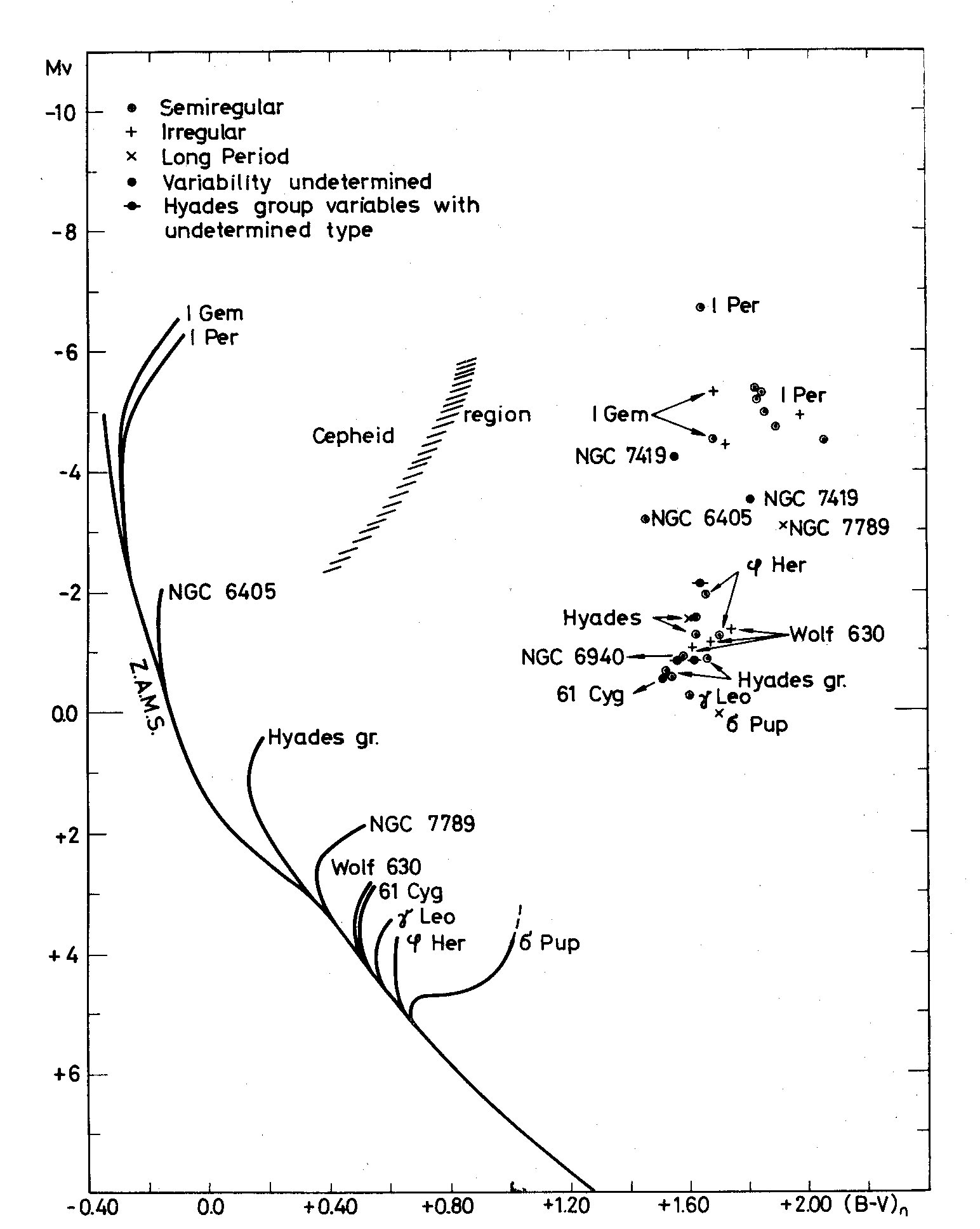 Fig. 2. H-R diagram of semiregular and irregular red variables. Schematic main
sequences of the corresponding clusters are also drawn.
So, either red variables are intrinsically more frequent in the first case, or
the stage of red variability is relatively longer for it. There is only one
ascertained case belonging to the second group, BM Sco in NGC 6405; the period
assigned to this variable is 850 days, much longer in respect to all others in
both groups; this fact suggests that this star, exceptional both for its
period and its location, should be studied more accurately.
On the whole, the present data, although insufficient, seem to support the
division of the red variables into two really different classes. The larger
mass one, whose evolution towards more unstable states as are the Miras seems
to be prevented by some other happening, might then perhaps be considered as
a possible candidate to represent the presupernova type II stage, should all
the present considerations correspond to some reality.
Table II
Cluster Star Mv kind of Period Spect. type (B-V)_0 Delta Mv Mass (H/M_hel) Age (years)
variability (days)
I Gem BU Gem -5.4 I - M1 Ia 1.68 1.4 < = 12 1*10^7
WY Gem -4.5 I - M3epIab 1.72 0.6 9 1*10^7
TV Gem -4.6 SR 182 M1 Iab 1.68 0.8 (1.4) 9 1*10^7
I Per YZ Per -6.8 SR 378 M2.5Iab 1.64 1.0 15+16 1.2*10^7
(h, chi) AD Per -5.5 SR 320 M2.5Iab 1.82 0.8 13 1.2*10^7
SU Per -5.2 SR 470 M3.5Iab 1.84 1.2 12 1.2*10^7
RS Per -5.3 SR 152 M4.5Iab 1.83 1.6 12 1.2*10^7
BU Per -5.0 SR 365 M3.5Ib 1.85 1.9 11 1.2*10^7
T Per -4.8 SR 326 M2Iab 1.89 1.0 10 1.2*10^7
S Per -4.6 SR - M4eIa 2.05 3.2 9 1.2*10^7
FZ Per -5.0 I - M1Iab 1.97 0.7 11 1.2*10^7
NGC 7419 -3.6 M7 1.80 9 8 2*10^7
-4.3 N (1) 1.55 9 9 2*10^7
NGC 6405 BM Sco (2) -3.2 SR 850 K-M 1.45 1.9 7 7*10^7
NGC 6940 -0.9 SR(I) (3) 80 M5II 1.58 2-3 4*10^8
Hyades (gr.) R Lyr -0.6 SR 46 M5III 1.52 ~1 2-3 4*10^8
R Hya -1.6 LPV 386 gM7e 1.60 6 2-3 4*10^8
VZ Cam -1.6 SR 23.7 gM4 1.62 0.3 2-3 4*10^8
RR UMi -0.6 SR 40(?) gM5III 1.54 0.3 2-3 4*10^8
TV Psc -0.1 SR 49 M3III 1.60 0.6 2-3 4*10^8
HR 46 -0.9 M3III 1.56 0.1 2-3 4*10^8
HR 1003 -0.9 gM3 1.62 0.1 2-3 4*10^8
HR 8636 -2.2 M3II 1.64 0.2 2-3 4*10^8
W Cyg -1.3 SR 130 gM4e-M6 1.62 2.1 2-3 4*10^8
NGC 7789 WY Cas -3.2 LPV 477 Se 1.91 >5.2 2 1.2*10^9
61 Cyg (gr.) -0.7 I gM6 1.53 1.3 3*10^9
zeta Herculis T Cet -2.0 SR 160 M5eII 1.65 1.1 1.2 ~(4-5)*10^9
(group) rho Per -1.3 SR 33-55 M4II-III 1.60 0.7 1.2 ~(4-5)*10^9
Wolf 630 (gr.) BQ Gem -1.2 I M4 1.67 0.4 1.2 ~(4-5)*10^9
-1.4 I M3S 1.74 1.2 ~(4-5)*10^9
-1.1 I gM1 1.61 1.2 ~(4-5)*10^9
gamma Leo (gr.) R Dor -0.3 SR 335 M7III 1.60 ~1 1.2 (4-5)*10^9
sigma Pup R Her 0.0 LPV 402 gm8e 1.70 ~10 < = 1 ~10^10
(1) Probably non member
(2) Possible member
(3) Uncertain.
Table III
Group Age limits (years) Mass limits Total Total Total Red variables
of clusters (solar unit) number number number
of clusters of red of red
giants variables red giant stars
I 5*10^6 < t < 2*10^7 M > = 9 16 37 13 0.35
II 2*10^7 < t < 2.5*10^8 3 < = M < = 9 47 184 1 0.005
III t > 2.5*10 M < 3 33 619 16 (22) 0.025 (0.035)
*
Our best thanks are due to Drs. G. Fabris and L. Nobili for their help
in collecting and discussing the material related to red semiregular and
irregular variables.
REFERENCES
Barbon, R., Dallaporta, N., Perissinotto, M. and Sussi, M. G. 1965, Mem. Soc.
astr. Ital. XXXVI, fasc. 1, 2.
Bertola, F., 1963, Contr. Oss. astrofis. Univ. Padova, N. 142 and 1965 N. 171.
Bertola, F. and Sussi, M. G., 1965, Contr. Oss. astrofis. Univ. Padova, N. 165.
Chiu, H. Y., 1961, Ann. of Phys. 15, 1; 16, 321.
Fraley, G. S., 1968, preprint.
Hayashi, C. and Cameron, R. C., 1962, Astrophys. J. 136, 166.
Hayashi, C., Hoshi, R. and Sugimoto, D., 1962, Prog. Theor. Phys. Suppl. N. 22.
Hoyle, F, and Flower, W. A., 1960, Astrophys. J. 132, 565.
Limber, D. N. 1960, Astrophys. J. 131, 168.
Minkowski, R., 1964, A. Rev. Astr. Astrophys. 2, 247.
Rakavy, G. and Shaviv, G., 1966, preprint.
Rakavy, G., Shaviv, G. and Zinamon, Z., 1967, Astrophys. J. 150, 131.
Weymann, R., 1961, Mt. Wilson and Palomar Obs. Spec. Techn. Rept. No. 4.
Zwicky, F., 1964, Astrophys. J. 137, 519.
Fig. 2. H-R diagram of semiregular and irregular red variables. Schematic main
sequences of the corresponding clusters are also drawn.
So, either red variables are intrinsically more frequent in the first case, or
the stage of red variability is relatively longer for it. There is only one
ascertained case belonging to the second group, BM Sco in NGC 6405; the period
assigned to this variable is 850 days, much longer in respect to all others in
both groups; this fact suggests that this star, exceptional both for its
period and its location, should be studied more accurately.
On the whole, the present data, although insufficient, seem to support the
division of the red variables into two really different classes. The larger
mass one, whose evolution towards more unstable states as are the Miras seems
to be prevented by some other happening, might then perhaps be considered as
a possible candidate to represent the presupernova type II stage, should all
the present considerations correspond to some reality.
Table II
Cluster Star Mv kind of Period Spect. type (B-V)_0 Delta Mv Mass (H/M_hel) Age (years)
variability (days)
I Gem BU Gem -5.4 I - M1 Ia 1.68 1.4 < = 12 1*10^7
WY Gem -4.5 I - M3epIab 1.72 0.6 9 1*10^7
TV Gem -4.6 SR 182 M1 Iab 1.68 0.8 (1.4) 9 1*10^7
I Per YZ Per -6.8 SR 378 M2.5Iab 1.64 1.0 15+16 1.2*10^7
(h, chi) AD Per -5.5 SR 320 M2.5Iab 1.82 0.8 13 1.2*10^7
SU Per -5.2 SR 470 M3.5Iab 1.84 1.2 12 1.2*10^7
RS Per -5.3 SR 152 M4.5Iab 1.83 1.6 12 1.2*10^7
BU Per -5.0 SR 365 M3.5Ib 1.85 1.9 11 1.2*10^7
T Per -4.8 SR 326 M2Iab 1.89 1.0 10 1.2*10^7
S Per -4.6 SR - M4eIa 2.05 3.2 9 1.2*10^7
FZ Per -5.0 I - M1Iab 1.97 0.7 11 1.2*10^7
NGC 7419 -3.6 M7 1.80 9 8 2*10^7
-4.3 N (1) 1.55 9 9 2*10^7
NGC 6405 BM Sco (2) -3.2 SR 850 K-M 1.45 1.9 7 7*10^7
NGC 6940 -0.9 SR(I) (3) 80 M5II 1.58 2-3 4*10^8
Hyades (gr.) R Lyr -0.6 SR 46 M5III 1.52 ~1 2-3 4*10^8
R Hya -1.6 LPV 386 gM7e 1.60 6 2-3 4*10^8
VZ Cam -1.6 SR 23.7 gM4 1.62 0.3 2-3 4*10^8
RR UMi -0.6 SR 40(?) gM5III 1.54 0.3 2-3 4*10^8
TV Psc -0.1 SR 49 M3III 1.60 0.6 2-3 4*10^8
HR 46 -0.9 M3III 1.56 0.1 2-3 4*10^8
HR 1003 -0.9 gM3 1.62 0.1 2-3 4*10^8
HR 8636 -2.2 M3II 1.64 0.2 2-3 4*10^8
W Cyg -1.3 SR 130 gM4e-M6 1.62 2.1 2-3 4*10^8
NGC 7789 WY Cas -3.2 LPV 477 Se 1.91 >5.2 2 1.2*10^9
61 Cyg (gr.) -0.7 I gM6 1.53 1.3 3*10^9
zeta Herculis T Cet -2.0 SR 160 M5eII 1.65 1.1 1.2 ~(4-5)*10^9
(group) rho Per -1.3 SR 33-55 M4II-III 1.60 0.7 1.2 ~(4-5)*10^9
Wolf 630 (gr.) BQ Gem -1.2 I M4 1.67 0.4 1.2 ~(4-5)*10^9
-1.4 I M3S 1.74 1.2 ~(4-5)*10^9
-1.1 I gM1 1.61 1.2 ~(4-5)*10^9
gamma Leo (gr.) R Dor -0.3 SR 335 M7III 1.60 ~1 1.2 (4-5)*10^9
sigma Pup R Her 0.0 LPV 402 gm8e 1.70 ~10 < = 1 ~10^10
(1) Probably non member
(2) Possible member
(3) Uncertain.
Table III
Group Age limits (years) Mass limits Total Total Total Red variables
of clusters (solar unit) number number number
of clusters of red of red
giants variables red giant stars
I 5*10^6 < t < 2*10^7 M > = 9 16 37 13 0.35
II 2*10^7 < t < 2.5*10^8 3 < = M < = 9 47 184 1 0.005
III t > 2.5*10 M < 3 33 619 16 (22) 0.025 (0.035)
*
Our best thanks are due to Drs. G. Fabris and L. Nobili for their help
in collecting and discussing the material related to red semiregular and
irregular variables.
REFERENCES
Barbon, R., Dallaporta, N., Perissinotto, M. and Sussi, M. G. 1965, Mem. Soc.
astr. Ital. XXXVI, fasc. 1, 2.
Bertola, F., 1963, Contr. Oss. astrofis. Univ. Padova, N. 142 and 1965 N. 171.
Bertola, F. and Sussi, M. G., 1965, Contr. Oss. astrofis. Univ. Padova, N. 165.
Chiu, H. Y., 1961, Ann. of Phys. 15, 1; 16, 321.
Fraley, G. S., 1968, preprint.
Hayashi, C. and Cameron, R. C., 1962, Astrophys. J. 136, 166.
Hayashi, C., Hoshi, R. and Sugimoto, D., 1962, Prog. Theor. Phys. Suppl. N. 22.
Hoyle, F, and Flower, W. A., 1960, Astrophys. J. 132, 565.
Limber, D. N. 1960, Astrophys. J. 131, 168.
Minkowski, R., 1964, A. Rev. Astr. Astrophys. 2, 247.
Rakavy, G. and Shaviv, G., 1966, preprint.
Rakavy, G., Shaviv, G. and Zinamon, Z., 1967, Astrophys. J. 150, 131.
Weymann, R., 1961, Mt. Wilson and Palomar Obs. Spec. Techn. Rept. No. 4.
Zwicky, F., 1964, Astrophys. J. 137, 519.
 Fig. 1. Evolutionary tracks for the core. M_b represents the mass of the
core; only for M_b > 1.41 the track crosses the Fe-He transition line.
Dashed region corresponds to the region of dynamical instability due to
the e^+ - e^- annihilation process.
An adequate investigation of the problem would require the detailed
treatment of core models of Rakavy-Shaviv's type with an hydrogen
envelope. In prevision of such a work, we try here to stress some points
showing, on very general arguments, the likelihood that the hydrogen
envelope persists throughout the whole presupernova stage and therefore
cannot be ignored for comparison with data. Finally, we discuss some possible
red supergiant types which could be suspected of being presupernova stages.
Concerning the first point, we first rely on the evolved models for large
mass stars (i.e. the 15.6 Msun star of Hayashi and Cameron (1962)) followed
from the main sequence to the initial phase of carbon burning. At this stage, the
star is left with a carbonoxygen core including the 18% of the total
mass. Assuming, as usual, that no conspicuous mass loss should alter the
evolution, one may try to calculate the maximum possible amount of
nuclear fuel which should be burnt in the interior of the star in the
remaining time of its supergiant evolution up to the last presupernova
stage; this should give us the maximum amount of hydrogen transformed
into heavier elements, and therefore allow to calculate the minimum
envelope which the star preserves just before its outburst.
The luminosity L_n due to nuclear shell burnings, is expressed by:
Fig. 1. Evolutionary tracks for the core. M_b represents the mass of the
core; only for M_b > 1.41 the track crosses the Fe-He transition line.
Dashed region corresponds to the region of dynamical instability due to
the e^+ - e^- annihilation process.
An adequate investigation of the problem would require the detailed
treatment of core models of Rakavy-Shaviv's type with an hydrogen
envelope. In prevision of such a work, we try here to stress some points
showing, on very general arguments, the likelihood that the hydrogen
envelope persists throughout the whole presupernova stage and therefore
cannot be ignored for comparison with data. Finally, we discuss some possible
red supergiant types which could be suspected of being presupernova stages.
Concerning the first point, we first rely on the evolved models for large
mass stars (i.e. the 15.6 Msun star of Hayashi and Cameron (1962)) followed
from the main sequence to the initial phase of carbon burning. At this stage, the
star is left with a carbonoxygen core including the 18% of the total
mass. Assuming, as usual, that no conspicuous mass loss should alter the
evolution, one may try to calculate the maximum possible amount of
nuclear fuel which should be burnt in the interior of the star in the
remaining time of its supergiant evolution up to the last presupernova
stage; this should give us the maximum amount of hydrogen transformed
into heavier elements, and therefore allow to calculate the minimum
envelope which the star preserves just before its outburst.
The luminosity L_n due to nuclear shell burnings, is expressed by:
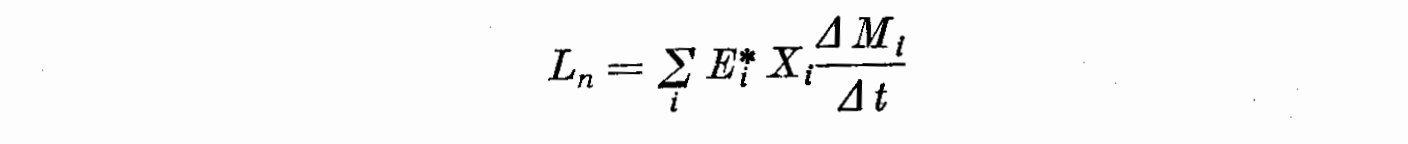 where E_i^* is the energy yield per gram of the i-th given fuel, X_i its
concentration in the i-th burning shell, Delta M_i / Delta t the
variation of mass of the i-th shell per unit time. The maximum value for
each of the Delta M_i may be immediately obtained by supposing its
corresponding shell as the only one burning, thus
where E_i^* is the energy yield per gram of the i-th given fuel, X_i its
concentration in the i-th burning shell, Delta M_i / Delta t the
variation of mass of the i-th shell per unit time. The maximum value for
each of the Delta M_i may be immediately obtained by supposing its
corresponding shell as the only one burning, thus
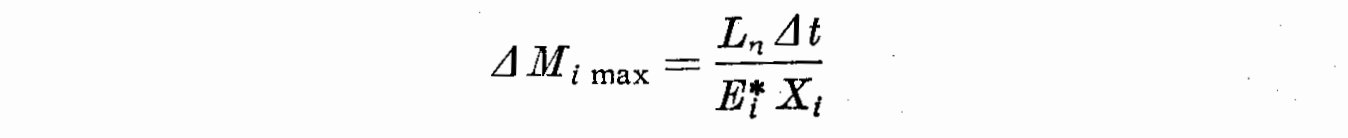 A more conservative assumption is reached by assuming an evolution in
which the different shells advance in a parallel way, the amounts of
different fuels burnt in each shell being approximately equal. That is,
we assume:
A more conservative assumption is reached by assuming an evolution in
which the different shells advance in a parallel way, the amounts of
different fuels burnt in each shell being approximately equal. That is,
we assume:
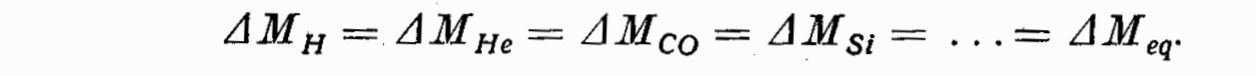 If we disregard the possible luminosity loss due to expansion of the
outer envelope which in no case (except flashes, not to be expected for
non degenerate matter) should be very large, and assuming that eventual
neutrino losses, however big, should be provided for by the central
burning of the core, the nuclear shell burnings luminosity L_n could be
substituted with the total observed luminosity L in order to arrive at
maximum estimations; thus we get:
If we disregard the possible luminosity loss due to expansion of the
outer envelope which in no case (except flashes, not to be expected for
non degenerate matter) should be very large, and assuming that eventual
neutrino losses, however big, should be provided for by the central
burning of the core, the nuclear shell burnings luminosity L_n could be
substituted with the total observed luminosity L in order to arrive at
maximum estimations; thus we get:
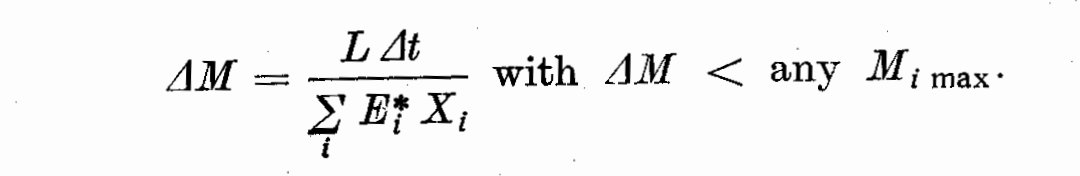 Assuming the data of the Hayashi model
Assuming the data of the Hayashi model
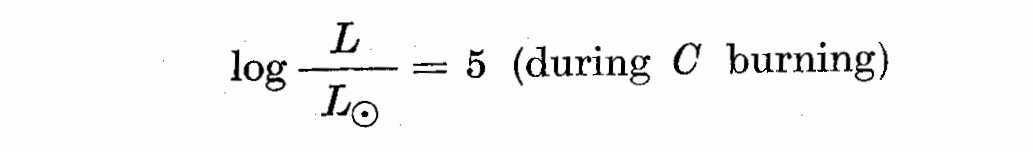 Delta t = 8 * 10^5 years from C burning to the explosion
and the constants tabulated in Table I, we obtain for the Delta M's the
results given also in Table I. These are probably rather insensitive to
errors of L and Delta t. Should in fact the luminosity increase due i.e. to
neutrino emission, then the evolution time Delta t should correspondingly
decrease, so that the product L Delta t would not change much.
If we define the core of the star as the central portion of it for which
mu = const ~ 2, that is the whole portion inside the He burning shell, then
according to data of Table I, the medium increase of it is Delta M / M = 0.06,
with extreme possibilities ranging from no increase at all
(should the He burning shell stop burning) and maximum increase of about 0.23
(should the He burn alone). The core fraction therefore should increase from
the 0.18 value in the last Hayashi model to 0.24+0.17-0.06
Table I
Delta t = 8 * 10^5 years from C burning to the explosion
and the constants tabulated in Table I, we obtain for the Delta M's the
results given also in Table I. These are probably rather insensitive to
errors of L and Delta t. Should in fact the luminosity increase due i.e. to
neutrino emission, then the evolution time Delta t should correspondingly
decrease, so that the product L Delta t would not change much.
If we define the core of the star as the central portion of it for which
mu = const ~ 2, that is the whole portion inside the He burning shell, then
according to data of Table I, the medium increase of it is Delta M / M = 0.06,
with extreme possibilities ranging from no increase at all
(should the He burning shell stop burning) and maximum increase of about 0.23
(should the He burn alone). The core fraction therefore should increase from
the 0.18 value in the last Hayashi model to 0.24+0.17-0.06
Table I
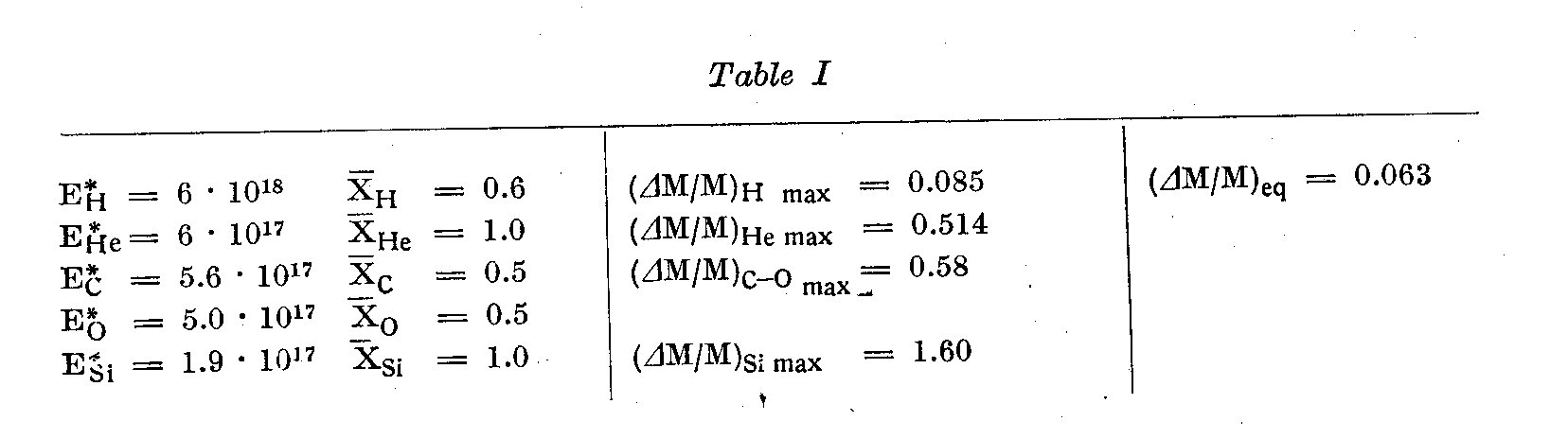 Should we instead consider the core as being only the innermost part
inside the deeper burning shell (at the end of the iron core), then only
a fraction of the previous increase is expected, which almost justifies
the assumption of a constant core made by Barbon et al.
If now, according to Rakavy and Shaviv, we consider that only cores with mass
greater than 2 Msun can surely evolve towards the Fe-He transition line (the
case of masses between 1.4 Msun and 2 Msun has not yet adequately studied by
these authors), then we obtain for the lower limit of the total mass of the
presupernova the value M_l ~- 8.3 Msun+2.7-3.3 with the first definition of
the core, and the value M_l ~ 11 Msun with the second one. Moreover, if we
accept Weymann's data (1961) on mass loss of red supergiants (20 per cent of
the total mass for alpha Ori), we obtain for the lower limits of the initial
masses of future type II supernovae the values M_l = 10.5+3.5-4.3 Msun
for the first type core definition, and M ~ 14 Msun for the other. Therefore,
the results of Barbon et al., on the mass range of type II supernovae, are
practically confirmed by the present analysis.
The absolute visual magnitude of a main sequence star with mass around
10-14 Msun lies in the range -3 to -4. According to Limber's (1960)
original luminosity function for the sun's neighbourhood, this gives us
for the number of stars per cubic parsec with luminosity higher than
this limit, the value ~1.10^-4. Assuming a mean lifetime for these stars
on the main sequence of T = 1.5 * 10^7 years, and equilibrium between
birth rate and death rate functions, we obtain some 0.7 * 10^-11 type II
supernovae per cubic parsec per year. Considering such events to occur
possibly in all the outer disc portion of the Galaxy, we arrive at a
frequency of a few events per year. Compared with data, this value is
too high by a factor of about 100. Considering, however, the enormous
uncertainty of the present evaluation, especially concerning the volume
of the galaxy occupied by population I, and the extrapolation of
the luminosity function for the sun's neighbourhood to the whole volume,
one cannot conclude that the present disagreement is sufficient to disprove
the theory. Moreover, it must be stressed that the present evaluation,
although too large greatly improves the figure obtained by lowering the
mass limit M, for supernovae to about 2 Msun as frequently done. Probably,
should the Fe-He conversion mechanism be true for triggering supernovae,
there should still be some other reason to further increase the lower
mass limit for their occurrence.
As a further remark, according to Rakavy and Shaviv, cores with mass
higher than ~ 30 Msun fail to reach the Fe--He transition line, as they
are stopped earlier in their evolutionary path by the e^+ - e^- pair
creation zone, in which the star grows unstable. The fate of such huge
stars has been investigated by Fraley (1968) and found to lead them to a
kind of softer collapse, which should perhaps show in a slower increase
of the light output at the beginning of the explosion. Such a situation
has been observed in some anomalous supernovae such as SN 96 in NGC 1058
discussed by Zwicky (1964) and Bertola (1963), which, moreover,
appears also at minimum to be an exceptionally luminous star (M_v ~= -9);
another example of the same type of event might have been eta Car. The
e^+ - e^- collapse might perhaps be taken into consideration for interpreting
such kind of events.
Concerning the second question of trying to identify the red supergiant
types which could be considered as last presupernova stages, we have
focused our attention on the red irregular and semiregular variables.
Although the difficulties of determining their low temperatures makes it
difficult to locate them exactly in the H-R diagram, still there may be
some suspicion that light variability occurs generally for the coolest
and reddest among giants, and this could connect its cause to the fact
of being near the Hayashi limit. If this were the case, and if the
evolutionary trend in the presupernova phase was still from left to
right in the H-R plane, then the connection of red variability with such
a phase could appear not too unlikely.
Not many reliable data on red variables of small amplitude are at hand.
In order to partially supply for this lack of knowledge, we have collected the
stars of this kind belonging to galactic clusters whose location in the H-R
plane is determined. The data concerning them are given in Table II and their
position in the H-R plane shown in Fig. 2; some Mira type stars belonging to
the clusters are included for comparison.
At first sight, the red variables appear to be divided into two groups:
an upper one of supergiants evolving from large mass clusters of early
population I; and a lower one of giants belonging to low mass clusters
of disk population. Mira variables are found only in this second group,
so that small amplitude red variables of this group could be considered
as transition stages leading to the Mira situation.
One would like to investigate whether the two groups outlined are in fact
physically different, and separated by a real gap between them. Some indication
on this question may be obtained from Table III, in which the clusters have
been divided into three groups according to their different ages, and which
contains the following data: number of clusters, number of red giants, number
of red variables, ratio of the number of variables to the total number of
giants for each group. The values into brackets for the third group include
stars which have not been studied yet and which, therefore, are only suspected
variables. It is seen that for the first or large mass group, the ratio of
column 4 is much higher than for the third or low mass group.
Should we instead consider the core as being only the innermost part
inside the deeper burning shell (at the end of the iron core), then only
a fraction of the previous increase is expected, which almost justifies
the assumption of a constant core made by Barbon et al.
If now, according to Rakavy and Shaviv, we consider that only cores with mass
greater than 2 Msun can surely evolve towards the Fe-He transition line (the
case of masses between 1.4 Msun and 2 Msun has not yet adequately studied by
these authors), then we obtain for the lower limit of the total mass of the
presupernova the value M_l ~- 8.3 Msun+2.7-3.3 with the first definition of
the core, and the value M_l ~ 11 Msun with the second one. Moreover, if we
accept Weymann's data (1961) on mass loss of red supergiants (20 per cent of
the total mass for alpha Ori), we obtain for the lower limits of the initial
masses of future type II supernovae the values M_l = 10.5+3.5-4.3 Msun
for the first type core definition, and M ~ 14 Msun for the other. Therefore,
the results of Barbon et al., on the mass range of type II supernovae, are
practically confirmed by the present analysis.
The absolute visual magnitude of a main sequence star with mass around
10-14 Msun lies in the range -3 to -4. According to Limber's (1960)
original luminosity function for the sun's neighbourhood, this gives us
for the number of stars per cubic parsec with luminosity higher than
this limit, the value ~1.10^-4. Assuming a mean lifetime for these stars
on the main sequence of T = 1.5 * 10^7 years, and equilibrium between
birth rate and death rate functions, we obtain some 0.7 * 10^-11 type II
supernovae per cubic parsec per year. Considering such events to occur
possibly in all the outer disc portion of the Galaxy, we arrive at a
frequency of a few events per year. Compared with data, this value is
too high by a factor of about 100. Considering, however, the enormous
uncertainty of the present evaluation, especially concerning the volume
of the galaxy occupied by population I, and the extrapolation of
the luminosity function for the sun's neighbourhood to the whole volume,
one cannot conclude that the present disagreement is sufficient to disprove
the theory. Moreover, it must be stressed that the present evaluation,
although too large greatly improves the figure obtained by lowering the
mass limit M, for supernovae to about 2 Msun as frequently done. Probably,
should the Fe-He conversion mechanism be true for triggering supernovae,
there should still be some other reason to further increase the lower
mass limit for their occurrence.
As a further remark, according to Rakavy and Shaviv, cores with mass
higher than ~ 30 Msun fail to reach the Fe--He transition line, as they
are stopped earlier in their evolutionary path by the e^+ - e^- pair
creation zone, in which the star grows unstable. The fate of such huge
stars has been investigated by Fraley (1968) and found to lead them to a
kind of softer collapse, which should perhaps show in a slower increase
of the light output at the beginning of the explosion. Such a situation
has been observed in some anomalous supernovae such as SN 96 in NGC 1058
discussed by Zwicky (1964) and Bertola (1963), which, moreover,
appears also at minimum to be an exceptionally luminous star (M_v ~= -9);
another example of the same type of event might have been eta Car. The
e^+ - e^- collapse might perhaps be taken into consideration for interpreting
such kind of events.
Concerning the second question of trying to identify the red supergiant
types which could be considered as last presupernova stages, we have
focused our attention on the red irregular and semiregular variables.
Although the difficulties of determining their low temperatures makes it
difficult to locate them exactly in the H-R diagram, still there may be
some suspicion that light variability occurs generally for the coolest
and reddest among giants, and this could connect its cause to the fact
of being near the Hayashi limit. If this were the case, and if the
evolutionary trend in the presupernova phase was still from left to
right in the H-R plane, then the connection of red variability with such
a phase could appear not too unlikely.
Not many reliable data on red variables of small amplitude are at hand.
In order to partially supply for this lack of knowledge, we have collected the
stars of this kind belonging to galactic clusters whose location in the H-R
plane is determined. The data concerning them are given in Table II and their
position in the H-R plane shown in Fig. 2; some Mira type stars belonging to
the clusters are included for comparison.
At first sight, the red variables appear to be divided into two groups:
an upper one of supergiants evolving from large mass clusters of early
population I; and a lower one of giants belonging to low mass clusters
of disk population. Mira variables are found only in this second group,
so that small amplitude red variables of this group could be considered
as transition stages leading to the Mira situation.
One would like to investigate whether the two groups outlined are in fact
physically different, and separated by a real gap between them. Some indication
on this question may be obtained from Table III, in which the clusters have
been divided into three groups according to their different ages, and which
contains the following data: number of clusters, number of red giants, number
of red variables, ratio of the number of variables to the total number of
giants for each group. The values into brackets for the third group include
stars which have not been studied yet and which, therefore, are only suspected
variables. It is seen that for the first or large mass group, the ratio of
column 4 is much higher than for the third or low mass group.
 Fig. 2. H-R diagram of semiregular and irregular red variables. Schematic main
sequences of the corresponding clusters are also drawn.
So, either red variables are intrinsically more frequent in the first case, or
the stage of red variability is relatively longer for it. There is only one
ascertained case belonging to the second group, BM Sco in NGC 6405; the period
assigned to this variable is 850 days, much longer in respect to all others in
both groups; this fact suggests that this star, exceptional both for its
period and its location, should be studied more accurately.
On the whole, the present data, although insufficient, seem to support the
division of the red variables into two really different classes. The larger
mass one, whose evolution towards more unstable states as are the Miras seems
to be prevented by some other happening, might then perhaps be considered as
a possible candidate to represent the presupernova type II stage, should all
the present considerations correspond to some reality.
Table II
Cluster Star Mv kind of Period Spect. type (B-V)_0 Delta Mv Mass (H/M_hel) Age (years)
variability (days)
I Gem BU Gem -5.4 I - M1 Ia 1.68 1.4 < = 12 1*10^7
WY Gem -4.5 I - M3epIab 1.72 0.6 9 1*10^7
TV Gem -4.6 SR 182 M1 Iab 1.68 0.8 (1.4) 9 1*10^7
I Per YZ Per -6.8 SR 378 M2.5Iab 1.64 1.0 15+16 1.2*10^7
(h, chi) AD Per -5.5 SR 320 M2.5Iab 1.82 0.8 13 1.2*10^7
SU Per -5.2 SR 470 M3.5Iab 1.84 1.2 12 1.2*10^7
RS Per -5.3 SR 152 M4.5Iab 1.83 1.6 12 1.2*10^7
BU Per -5.0 SR 365 M3.5Ib 1.85 1.9 11 1.2*10^7
T Per -4.8 SR 326 M2Iab 1.89 1.0 10 1.2*10^7
S Per -4.6 SR - M4eIa 2.05 3.2 9 1.2*10^7
FZ Per -5.0 I - M1Iab 1.97 0.7 11 1.2*10^7
NGC 7419 -3.6 M7 1.80 9 8 2*10^7
-4.3 N (1) 1.55 9 9 2*10^7
NGC 6405 BM Sco (2) -3.2 SR 850 K-M 1.45 1.9 7 7*10^7
NGC 6940 -0.9 SR(I) (3) 80 M5II 1.58 2-3 4*10^8
Hyades (gr.) R Lyr -0.6 SR 46 M5III 1.52 ~1 2-3 4*10^8
R Hya -1.6 LPV 386 gM7e 1.60 6 2-3 4*10^8
VZ Cam -1.6 SR 23.7 gM4 1.62 0.3 2-3 4*10^8
RR UMi -0.6 SR 40(?) gM5III 1.54 0.3 2-3 4*10^8
TV Psc -0.1 SR 49 M3III 1.60 0.6 2-3 4*10^8
HR 46 -0.9 M3III 1.56 0.1 2-3 4*10^8
HR 1003 -0.9 gM3 1.62 0.1 2-3 4*10^8
HR 8636 -2.2 M3II 1.64 0.2 2-3 4*10^8
W Cyg -1.3 SR 130 gM4e-M6 1.62 2.1 2-3 4*10^8
NGC 7789 WY Cas -3.2 LPV 477 Se 1.91 >5.2 2 1.2*10^9
61 Cyg (gr.) -0.7 I gM6 1.53 1.3 3*10^9
zeta Herculis T Cet -2.0 SR 160 M5eII 1.65 1.1 1.2 ~(4-5)*10^9
(group) rho Per -1.3 SR 33-55 M4II-III 1.60 0.7 1.2 ~(4-5)*10^9
Wolf 630 (gr.) BQ Gem -1.2 I M4 1.67 0.4 1.2 ~(4-5)*10^9
-1.4 I M3S 1.74 1.2 ~(4-5)*10^9
-1.1 I gM1 1.61 1.2 ~(4-5)*10^9
gamma Leo (gr.) R Dor -0.3 SR 335 M7III 1.60 ~1 1.2 (4-5)*10^9
sigma Pup R Her 0.0 LPV 402 gm8e 1.70 ~10 < = 1 ~10^10
(1) Probably non member
(2) Possible member
(3) Uncertain.
Table III
Group Age limits (years) Mass limits Total Total Total Red variables
of clusters (solar unit) number number number
of clusters of red of red
giants variables red giant stars
I 5*10^6 < t < 2*10^7 M > = 9 16 37 13 0.35
II 2*10^7 < t < 2.5*10^8 3 < = M < = 9 47 184 1 0.005
III t > 2.5*10 M < 3 33 619 16 (22) 0.025 (0.035)
*
Our best thanks are due to Drs. G. Fabris and L. Nobili for their help
in collecting and discussing the material related to red semiregular and
irregular variables.
REFERENCES
Barbon, R., Dallaporta, N., Perissinotto, M. and Sussi, M. G. 1965, Mem. Soc.
astr. Ital. XXXVI, fasc. 1, 2.
Bertola, F., 1963, Contr. Oss. astrofis. Univ. Padova, N. 142 and 1965 N. 171.
Bertola, F. and Sussi, M. G., 1965, Contr. Oss. astrofis. Univ. Padova, N. 165.
Chiu, H. Y., 1961, Ann. of Phys. 15, 1; 16, 321.
Fraley, G. S., 1968, preprint.
Hayashi, C. and Cameron, R. C., 1962, Astrophys. J. 136, 166.
Hayashi, C., Hoshi, R. and Sugimoto, D., 1962, Prog. Theor. Phys. Suppl. N. 22.
Hoyle, F, and Flower, W. A., 1960, Astrophys. J. 132, 565.
Limber, D. N. 1960, Astrophys. J. 131, 168.
Minkowski, R., 1964, A. Rev. Astr. Astrophys. 2, 247.
Rakavy, G. and Shaviv, G., 1966, preprint.
Rakavy, G., Shaviv, G. and Zinamon, Z., 1967, Astrophys. J. 150, 131.
Weymann, R., 1961, Mt. Wilson and Palomar Obs. Spec. Techn. Rept. No. 4.
Zwicky, F., 1964, Astrophys. J. 137, 519.
Fig. 2. H-R diagram of semiregular and irregular red variables. Schematic main
sequences of the corresponding clusters are also drawn.
So, either red variables are intrinsically more frequent in the first case, or
the stage of red variability is relatively longer for it. There is only one
ascertained case belonging to the second group, BM Sco in NGC 6405; the period
assigned to this variable is 850 days, much longer in respect to all others in
both groups; this fact suggests that this star, exceptional both for its
period and its location, should be studied more accurately.
On the whole, the present data, although insufficient, seem to support the
division of the red variables into two really different classes. The larger
mass one, whose evolution towards more unstable states as are the Miras seems
to be prevented by some other happening, might then perhaps be considered as
a possible candidate to represent the presupernova type II stage, should all
the present considerations correspond to some reality.
Table II
Cluster Star Mv kind of Period Spect. type (B-V)_0 Delta Mv Mass (H/M_hel) Age (years)
variability (days)
I Gem BU Gem -5.4 I - M1 Ia 1.68 1.4 < = 12 1*10^7
WY Gem -4.5 I - M3epIab 1.72 0.6 9 1*10^7
TV Gem -4.6 SR 182 M1 Iab 1.68 0.8 (1.4) 9 1*10^7
I Per YZ Per -6.8 SR 378 M2.5Iab 1.64 1.0 15+16 1.2*10^7
(h, chi) AD Per -5.5 SR 320 M2.5Iab 1.82 0.8 13 1.2*10^7
SU Per -5.2 SR 470 M3.5Iab 1.84 1.2 12 1.2*10^7
RS Per -5.3 SR 152 M4.5Iab 1.83 1.6 12 1.2*10^7
BU Per -5.0 SR 365 M3.5Ib 1.85 1.9 11 1.2*10^7
T Per -4.8 SR 326 M2Iab 1.89 1.0 10 1.2*10^7
S Per -4.6 SR - M4eIa 2.05 3.2 9 1.2*10^7
FZ Per -5.0 I - M1Iab 1.97 0.7 11 1.2*10^7
NGC 7419 -3.6 M7 1.80 9 8 2*10^7
-4.3 N (1) 1.55 9 9 2*10^7
NGC 6405 BM Sco (2) -3.2 SR 850 K-M 1.45 1.9 7 7*10^7
NGC 6940 -0.9 SR(I) (3) 80 M5II 1.58 2-3 4*10^8
Hyades (gr.) R Lyr -0.6 SR 46 M5III 1.52 ~1 2-3 4*10^8
R Hya -1.6 LPV 386 gM7e 1.60 6 2-3 4*10^8
VZ Cam -1.6 SR 23.7 gM4 1.62 0.3 2-3 4*10^8
RR UMi -0.6 SR 40(?) gM5III 1.54 0.3 2-3 4*10^8
TV Psc -0.1 SR 49 M3III 1.60 0.6 2-3 4*10^8
HR 46 -0.9 M3III 1.56 0.1 2-3 4*10^8
HR 1003 -0.9 gM3 1.62 0.1 2-3 4*10^8
HR 8636 -2.2 M3II 1.64 0.2 2-3 4*10^8
W Cyg -1.3 SR 130 gM4e-M6 1.62 2.1 2-3 4*10^8
NGC 7789 WY Cas -3.2 LPV 477 Se 1.91 >5.2 2 1.2*10^9
61 Cyg (gr.) -0.7 I gM6 1.53 1.3 3*10^9
zeta Herculis T Cet -2.0 SR 160 M5eII 1.65 1.1 1.2 ~(4-5)*10^9
(group) rho Per -1.3 SR 33-55 M4II-III 1.60 0.7 1.2 ~(4-5)*10^9
Wolf 630 (gr.) BQ Gem -1.2 I M4 1.67 0.4 1.2 ~(4-5)*10^9
-1.4 I M3S 1.74 1.2 ~(4-5)*10^9
-1.1 I gM1 1.61 1.2 ~(4-5)*10^9
gamma Leo (gr.) R Dor -0.3 SR 335 M7III 1.60 ~1 1.2 (4-5)*10^9
sigma Pup R Her 0.0 LPV 402 gm8e 1.70 ~10 < = 1 ~10^10
(1) Probably non member
(2) Possible member
(3) Uncertain.
Table III
Group Age limits (years) Mass limits Total Total Total Red variables
of clusters (solar unit) number number number
of clusters of red of red
giants variables red giant stars
I 5*10^6 < t < 2*10^7 M > = 9 16 37 13 0.35
II 2*10^7 < t < 2.5*10^8 3 < = M < = 9 47 184 1 0.005
III t > 2.5*10 M < 3 33 619 16 (22) 0.025 (0.035)
*
Our best thanks are due to Drs. G. Fabris and L. Nobili for their help
in collecting and discussing the material related to red semiregular and
irregular variables.
REFERENCES
Barbon, R., Dallaporta, N., Perissinotto, M. and Sussi, M. G. 1965, Mem. Soc.
astr. Ital. XXXVI, fasc. 1, 2.
Bertola, F., 1963, Contr. Oss. astrofis. Univ. Padova, N. 142 and 1965 N. 171.
Bertola, F. and Sussi, M. G., 1965, Contr. Oss. astrofis. Univ. Padova, N. 165.
Chiu, H. Y., 1961, Ann. of Phys. 15, 1; 16, 321.
Fraley, G. S., 1968, preprint.
Hayashi, C. and Cameron, R. C., 1962, Astrophys. J. 136, 166.
Hayashi, C., Hoshi, R. and Sugimoto, D., 1962, Prog. Theor. Phys. Suppl. N. 22.
Hoyle, F, and Flower, W. A., 1960, Astrophys. J. 132, 565.
Limber, D. N. 1960, Astrophys. J. 131, 168.
Minkowski, R., 1964, A. Rev. Astr. Astrophys. 2, 247.
Rakavy, G. and Shaviv, G., 1966, preprint.
Rakavy, G., Shaviv, G. and Zinamon, Z., 1967, Astrophys. J. 150, 131.
Weymann, R., 1961, Mt. Wilson and Palomar Obs. Spec. Techn. Rept. No. 4.
Zwicky, F., 1964, Astrophys. J. 137, 519.