Non-Periodic Phenomena in Variable Stars
IAU Colloquium, Budapest, 1968
TIDAL RESONANCES IN SOME PULSATION MODES OF THE BETA
CANIS MAJORIS STAR 16 LACERTAE
W. S. FITCH
Steward Observatory, Tucson, Arizona, USA
Analyses by Fitch (1967) of the published observational data on the delta
Scuti star CC Andromedae and the beta Canis Majoris star sigma Scorpii led to
the suggestion that the often observed presence of multiple periodicities in
these kinds of stars should be attributed to the influence on the normal
pulsation mode of structural changes produced in the outer layers of the
pulsating primary by tidal perturbations due to a faint companion. This
suggestion is further supported by Preston's (1966) announcement at the 3rd
Variable Star Colloquium that the delta Scuti star delta Delphini is a
double-line spectroscopic binary.
In a continuation of work on this problem the beta Canis Majoris star
16 Lacertae, whose intrinsic variability was discovered by Walker (1951).
was selected because very extensive observational material had been published.
This star was announced by Struve and Bobrovnikoff (1925) as a single-line
spectroscopic binary with a period of 12.3106 days, but the observations here
analysed are the radial velocity measures obtained on 26 nights in 1951 by
Struve, McNamara, Kraft, Kung, and Williams (1952), together with the
data contained in the radial velocity and blue light curves published by Walker
(1951, 1952, 1954). Because the original lists of the photoelectric measures
have been lost (Walker 1967), it was necessary to read the observations from
photographic enlargements of the published light curves, and it is expected that
these measures, which are consequently less accurate than the originals, will
be made available to interested workers by inclusion in the IAU (27). RAS.
file of the Royal Astronomical Society Library. All of Walker's blue magnitude
measures (7 nights in 1950, 13 nights in 1951, and 10 nights in 1952) were
employed, except that the two nights of 16 and 17 August 1951 were never
included because of the very low signal-to-noise ratio evident in the light
curves for these nights. A single velocity curve published by Walker (1954)
was read in the same fashion and included in the velocity analysis, but a second
velocity curve which Walker (1951) published was inadvertently skipped.
A preliminary periodogram analysis (Wehlau and Leung 1964; Fitch 1967)
confirmed the primary period reported by previous workers, and a frequency of
5.9113 cycles day (c/d) with a corresponding period of 0.169168 day was adopted
as best fitting these observation. With this frequency the light and/or velocity
measures on each night were individually fitted by least squares to obtain the
amplitude, phase, and mean value best representing a sinusoidal variation on
each night. The nightly velocity means were then fitted by least squares in
our spectroscopic binary program to yield these orbital elements with their
probable errors:
P = 12.079 +- 0.005 days e = 0.012 +- 0.02
T_0 = JD 2433872 +- 2.6 days omega = 121 deg +- 79 deg
gamma = -13.0 +- 0.6 km/sec f(M) = 0.0147 M_hel
K_1 = 22.7 +- 0.4 km/sec a_1 sin i = 3.77 X 10^6 km
The corresponding velocity curve is shown in Figure 1.
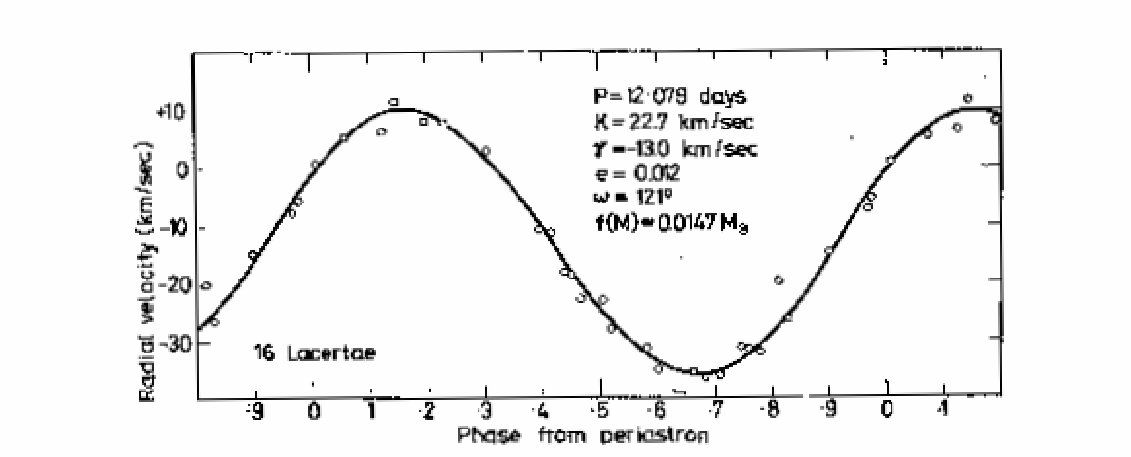 Fig. 1. The orbital radial velocity variation of the primary component of 16 Lacertae.
The plotted points are mean velocity measures for individual nights and the full curve
is the computed solution.
The nightly luminosity means vary strongly in an apparently erratic
fashion which we were unable to correlate with the orbital motion, and since
the comparison star 14 Lacertae has been reported to be variable (Walker
1952, 1953), it was necessary to attribute these variations in the mean light
level to 14 Lacertae and to compensate for them by applying night corrections
deduced from the mean values of the luminosity ratio. This arbitrary correction
procedure automatically precludes the possibility of finding any light variation
which depends solely on the orbital motion.
When the velocity and light measures had been freed of the principal
slow variations by means of the known orbital motion (here represented as
a sinusoidal velocity variation with frequency n_0 = 0.08279 c/d) and the
night corrections, respectively, further periodogram analysis disclosed the
existence of two more periodic variations (frequencies n_2 = 5.8529 and n_3 =
= 5.4998 c/d, in addition to the primary frequency n_1 = 5.9113 c/d) in both
the light and velocity observations. The three photometric observing seasons
were from J.D. 2433504 to 2433536, 2433870 to 2433926, and 2434231 to
2434242, while we have divided the principal velocity observing season in
two halves running from 2433869 to 2433926 and 2433937 to 2433967. The
principal data relating to these variations is summarized in Tables 1 and 2,
in which it is seen that the velocity-to-light amplitude ratio is much larger
for n_1 than for n_2 and n_3 (about 6.0, 3.0, and 1.5 km/sec percent mean light,
respectively), and also that the amplitude of n_3 varies strongly and apparently
concordantly in both light and velocity measures. The former observation
is illustrated by Figures 2 and 3, which show from the results of fitting to
simultaneous light and velocity measures obtained on 11 nights that both
amplitude and phase perturbations of the primary pulsation are much stronger
in light than in velocity, while the latter conclusion suggests the possibility
of long period interference effects arising from a close frequency doublet.
Since the annual cycle count is uncertain due to the very short photometric
observing seasons, the pulsation frequencies derived by periodogram analysis
could be in error by one cycle per year = 0.0027 c/d, though they are otherwise
accurate to +-0.0002 c/d or better. A proper change of 0.0027 c/d in n_2 and
in n_3 would in each case produce a nearly perfect tidal resonance, so exact
resonances were assumed and subsequent periodogram analysis disclosed the
existence in the light and velocity variations of the corresponding doublet
components of frequencies n_2 and n_3, as shown in Table 3.
Table 1
Blue Light Variation of 16 Lacertae
Frequency Blue Light Range (%) Phase Zero Point (Periods) M. E.
Year 5.9113 5.8529 5.4998 5.9113 5.8529 5.4998 of 1 obs. No. of Obs.
1950 ........... 4.8 2.3 3.1 0.590 0.281 0.565 1.6 242
1951 ........... 4.6 2.4 0.3 0.617 0.242 0.567 0.7 473
1952 4.5 2.5 2.7 0.618 0.225 0.550 0.8 452
1950, 1952 4.5 2.5 2.7 0.611 0.231 0.560 1.1 694
1950, 51, 52 4.7 2.4 1.9 0.612 0.235 0.560 1.0 1167
Table 2
Velocity Variation of 16 Lacertae
Frequency Velocity Range (km/sec) Phase Zero Point (Periods) M. E.
Year 5.9113 5.8529 5.4998 5.9113 5.8529 5.4998 of 1 obs. No. of Obs.
1951-1st 1/2 27.5 6.8 0.8 0.857 0.503 0.895 3.5 234
1951-2nd 1/2 29.3 7.2 4.1 0.852 0.548 0.864 3.5 208
All 1951 28.3 6.9 2.2 0.854 0.516 0.876 3.6 442
1951, 1952 28.6 7.2 2.3 0.855 0.514 0.885 3.6 456
Fig. 1. The orbital radial velocity variation of the primary component of 16 Lacertae.
The plotted points are mean velocity measures for individual nights and the full curve
is the computed solution.
The nightly luminosity means vary strongly in an apparently erratic
fashion which we were unable to correlate with the orbital motion, and since
the comparison star 14 Lacertae has been reported to be variable (Walker
1952, 1953), it was necessary to attribute these variations in the mean light
level to 14 Lacertae and to compensate for them by applying night corrections
deduced from the mean values of the luminosity ratio. This arbitrary correction
procedure automatically precludes the possibility of finding any light variation
which depends solely on the orbital motion.
When the velocity and light measures had been freed of the principal
slow variations by means of the known orbital motion (here represented as
a sinusoidal velocity variation with frequency n_0 = 0.08279 c/d) and the
night corrections, respectively, further periodogram analysis disclosed the
existence of two more periodic variations (frequencies n_2 = 5.8529 and n_3 =
= 5.4998 c/d, in addition to the primary frequency n_1 = 5.9113 c/d) in both
the light and velocity observations. The three photometric observing seasons
were from J.D. 2433504 to 2433536, 2433870 to 2433926, and 2434231 to
2434242, while we have divided the principal velocity observing season in
two halves running from 2433869 to 2433926 and 2433937 to 2433967. The
principal data relating to these variations is summarized in Tables 1 and 2,
in which it is seen that the velocity-to-light amplitude ratio is much larger
for n_1 than for n_2 and n_3 (about 6.0, 3.0, and 1.5 km/sec percent mean light,
respectively), and also that the amplitude of n_3 varies strongly and apparently
concordantly in both light and velocity measures. The former observation
is illustrated by Figures 2 and 3, which show from the results of fitting to
simultaneous light and velocity measures obtained on 11 nights that both
amplitude and phase perturbations of the primary pulsation are much stronger
in light than in velocity, while the latter conclusion suggests the possibility
of long period interference effects arising from a close frequency doublet.
Since the annual cycle count is uncertain due to the very short photometric
observing seasons, the pulsation frequencies derived by periodogram analysis
could be in error by one cycle per year = 0.0027 c/d, though they are otherwise
accurate to +-0.0002 c/d or better. A proper change of 0.0027 c/d in n_2 and
in n_3 would in each case produce a nearly perfect tidal resonance, so exact
resonances were assumed and subsequent periodogram analysis disclosed the
existence in the light and velocity variations of the corresponding doublet
components of frequencies n_2 and n_3, as shown in Table 3.
Table 1
Blue Light Variation of 16 Lacertae
Frequency Blue Light Range (%) Phase Zero Point (Periods) M. E.
Year 5.9113 5.8529 5.4998 5.9113 5.8529 5.4998 of 1 obs. No. of Obs.
1950 ........... 4.8 2.3 3.1 0.590 0.281 0.565 1.6 242
1951 ........... 4.6 2.4 0.3 0.617 0.242 0.567 0.7 473
1952 4.5 2.5 2.7 0.618 0.225 0.550 0.8 452
1950, 1952 4.5 2.5 2.7 0.611 0.231 0.560 1.1 694
1950, 51, 52 4.7 2.4 1.9 0.612 0.235 0.560 1.0 1167
Table 2
Velocity Variation of 16 Lacertae
Frequency Velocity Range (km/sec) Phase Zero Point (Periods) M. E.
Year 5.9113 5.8529 5.4998 5.9113 5.8529 5.4998 of 1 obs. No. of Obs.
1951-1st 1/2 27.5 6.8 0.8 0.857 0.503 0.895 3.5 234
1951-2nd 1/2 29.3 7.2 4.1 0.852 0.548 0.864 3.5 208
All 1951 28.3 6.9 2.2 0.854 0.516 0.876 3.6 442
1951, 1952 28.6 7.2 2.3 0.855 0.514 0.885 3.6 456
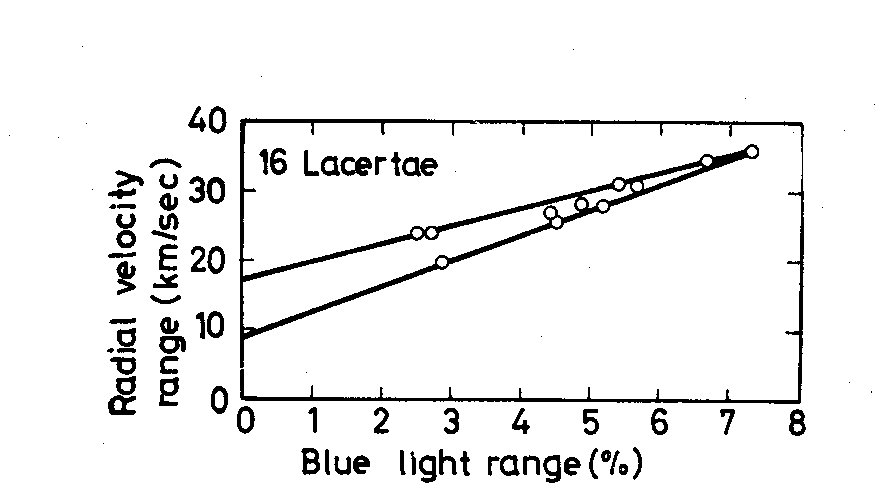 Fig. 2. A comparison of the variations
in radial velocity and blue light ranges
of the primary pulsation, as determined
by simultaneous observations on 11 nights.
Extrapolations of the straight lines bounding
the observed region do not enclose the origin.
Fig. 2. A comparison of the variations
in radial velocity and blue light ranges
of the primary pulsation, as determined
by simultaneous observations on 11 nights.
Extrapolations of the straight lines bounding
the observed region do not enclose the origin.
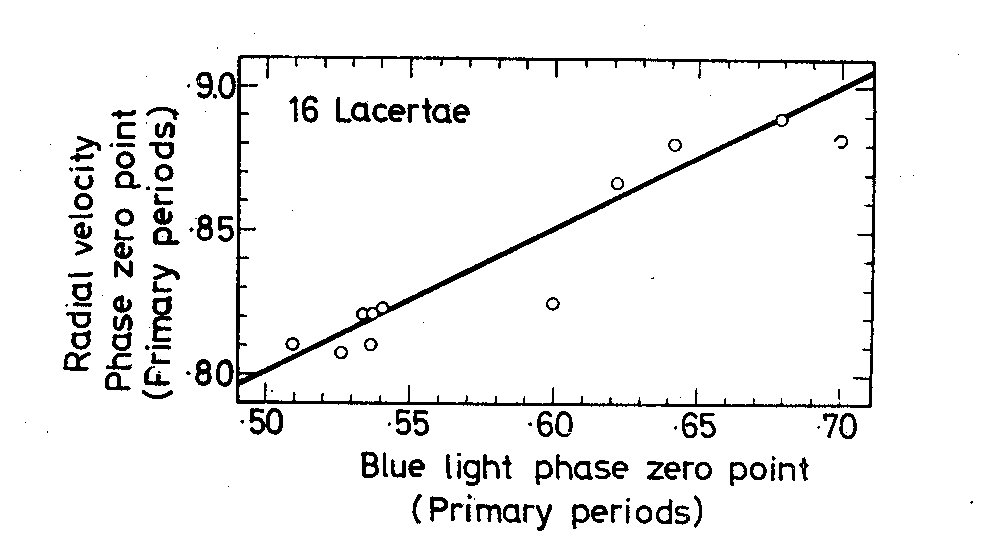 Fig. 3. A comparison of the variations in radial
velocity and blue light of the primary pulsation's
phase zero point, as determined by simultaneous
observations on 11 nights. The straight line was
drawn with slope 1/2.
Table 3.
Adopted Solution for 16 Lacertae
Frequency Description Half Range Phase Zero Point
(c/d) (km/sec) (% light) R. V. Light
5.9177 n_3 + 5n_0 0.3 0.26 0.11 0.41
5.9113 n_1 14.4 2.41 0.85 0.63
5.9048 n_2 + 2/3n_0 0.8 0.24 0.06 0.89
5.8561 n_1 - 2/3n_0 2.9 0.70 0.56 0.42
5.8496 n_2 2.2 0.76 0.57 0.20
5.5037 n_3 1.0 0.82 0.23 0.79
5.4973 n_1 - 5n_0 0.9 0.83 0.16 0.60
0.08279 n_0 22.9 0.88
0.1656 2n_0 0.7 0.21
0.2484 3n_0 0.5 0.39
0.3312 4n_0 1.2 0.08
To explain this result, we consider a system of N coupled linear oscillators,
in which the state of the k^th oscillator (of natural frequency n_k) is specified
by the generalized coordinate q_k, and on which an external periodic force F
of frequency n_0 (where n_0 << n_k) acts. We assume we can expand each
component of F in a Fourier series harmonic in n_0, so that, neglecting both
the direct response of the system to the imposed force F and non-linear terms
in the coordinates q_k, we have
Fig. 3. A comparison of the variations in radial
velocity and blue light of the primary pulsation's
phase zero point, as determined by simultaneous
observations on 11 nights. The straight line was
drawn with slope 1/2.
Table 3.
Adopted Solution for 16 Lacertae
Frequency Description Half Range Phase Zero Point
(c/d) (km/sec) (% light) R. V. Light
5.9177 n_3 + 5n_0 0.3 0.26 0.11 0.41
5.9113 n_1 14.4 2.41 0.85 0.63
5.9048 n_2 + 2/3n_0 0.8 0.24 0.06 0.89
5.8561 n_1 - 2/3n_0 2.9 0.70 0.56 0.42
5.8496 n_2 2.2 0.76 0.57 0.20
5.5037 n_3 1.0 0.82 0.23 0.79
5.4973 n_1 - 5n_0 0.9 0.83 0.16 0.60
0.08279 n_0 22.9 0.88
0.1656 2n_0 0.7 0.21
0.2484 3n_0 0.5 0.39
0.3312 4n_0 1.2 0.08
To explain this result, we consider a system of N coupled linear oscillators,
in which the state of the k^th oscillator (of natural frequency n_k) is specified
by the generalized coordinate q_k, and on which an external periodic force F
of frequency n_0 (where n_0 << n_k) acts. We assume we can expand each
component of F in a Fourier series harmonic in n_0, so that, neglecting both
the direct response of the system to the imposed force F and non-linear terms
in the coordinates q_k, we have
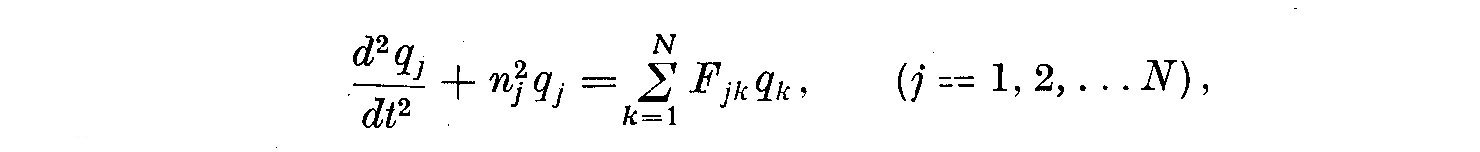 (1)
where
(1)
where
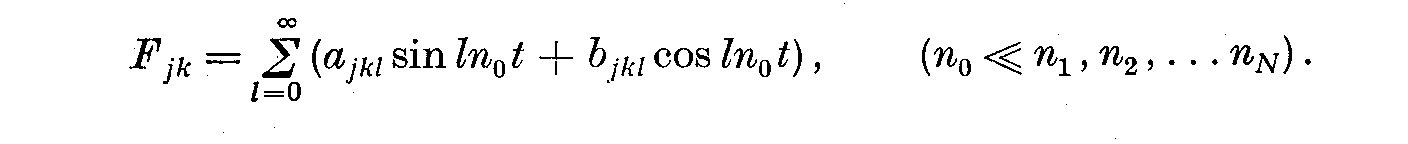 (2)
It is easily shown that the periodic solutions of these equations, complete to
the second order, may be written in the form
(2)
It is easily shown that the periodic solutions of these equations, complete to
the second order, may be written in the form
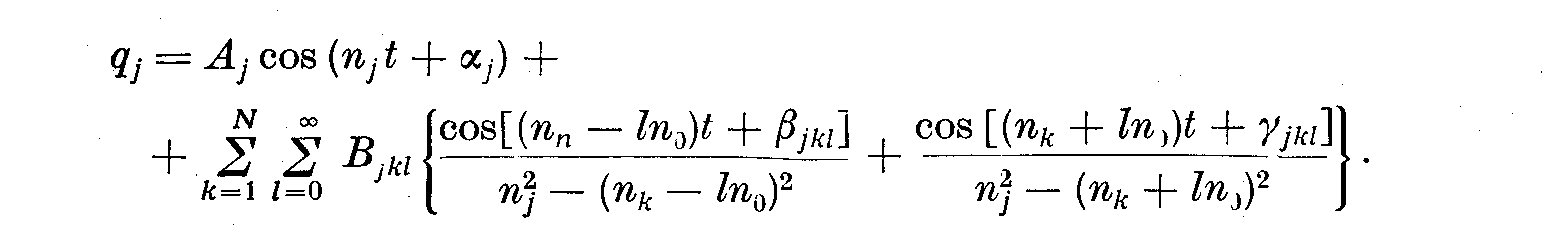 (3)
Thus the solution will contain both the natural frequencies n_k and also the
combination terms n_k +- ln_0 but of the latter the most important are likely
to be those (if any) for which a near resonance exists (i.e. [n_k +- ln_0]^2 ~~n^2_j).
Of course, terms with the forcing frequencies ln_0 which were neglected in
equations (1), will also exist. Our foregoing argument for the resonance case
requires, strictly speaking, that l be integer, but as is well known, resonance
often occurs when l is rational, provided it is the quotient of two small integers
(e.g. the Kirkwood gaps and the Hilda group in the case of the asteroids). In
the present case, with P_0 as the orbital period in a nearly (or perhaps exactly)
circular orbit, the tidal perturbations are nearly the same at intervals of
1/2 P_0, P_0 and 3/2 P_0, so that the strongest perturbing frequencies should be
2n_0, n_0, and 2/3 n_0.
Since the two resonance pairs of difference frequencies (n_2, n_1 - 2/3 n_0)
and (n_3, n_1 - 5n_0) had been observed, in accordance with the preceding analysis
the corresponding sum frequencies n_2 + 2/3 n_0 and n_3 + 5 n_0 were included
in the least squares fitting for the adopted solution displayed in Table 3.
That these sum terms are of very small amplitude (and perhaps not present)
is not surprising, since they arise from tidal action on the very weak terms
n_2 and n_3, whereas the difference terms here originate in the action of F on n_1.
The ordinary, non-resonant combination terms n_1 +- ln_0, were also included
in a fitting with l = 1, 2, and 3, and are probably present but are of too small
amplitude to be significant. We note that n_3 - (n_1 - 5n_0) = +0.0064 c/d and
n_2 - (n_1- 2/3 n_0) = -0.0065 c/d, with errors probably not exceeding
+- 0.0002 c/d, so that the detuning effect on the primary frequency n_1 is almost
exactly cancelled by the opposing actions of the two resonance terms.
In figures 4, 5 and 6 we illustrate the agreement between the adopted
radial velocity solution and the observations, and in figures 7, 8 and 9 the
same comparison is made for the light variation. For the velocities only on
the first night does the solution appear unsatisfactory, and it was just this
night that showed the large residual on the radial velocity curve. The representation
of the observed light variation appears generally satisfactory except for the
last night in the first (1950) observing season. But since the signalto-noise
ratio for this first season is much lower than in 1951 and 1952, it is not
certain that the discrepancies here are significant.
(3)
Thus the solution will contain both the natural frequencies n_k and also the
combination terms n_k +- ln_0 but of the latter the most important are likely
to be those (if any) for which a near resonance exists (i.e. [n_k +- ln_0]^2 ~~n^2_j).
Of course, terms with the forcing frequencies ln_0 which were neglected in
equations (1), will also exist. Our foregoing argument for the resonance case
requires, strictly speaking, that l be integer, but as is well known, resonance
often occurs when l is rational, provided it is the quotient of two small integers
(e.g. the Kirkwood gaps and the Hilda group in the case of the asteroids). In
the present case, with P_0 as the orbital period in a nearly (or perhaps exactly)
circular orbit, the tidal perturbations are nearly the same at intervals of
1/2 P_0, P_0 and 3/2 P_0, so that the strongest perturbing frequencies should be
2n_0, n_0, and 2/3 n_0.
Since the two resonance pairs of difference frequencies (n_2, n_1 - 2/3 n_0)
and (n_3, n_1 - 5n_0) had been observed, in accordance with the preceding analysis
the corresponding sum frequencies n_2 + 2/3 n_0 and n_3 + 5 n_0 were included
in the least squares fitting for the adopted solution displayed in Table 3.
That these sum terms are of very small amplitude (and perhaps not present)
is not surprising, since they arise from tidal action on the very weak terms
n_2 and n_3, whereas the difference terms here originate in the action of F on n_1.
The ordinary, non-resonant combination terms n_1 +- ln_0, were also included
in a fitting with l = 1, 2, and 3, and are probably present but are of too small
amplitude to be significant. We note that n_3 - (n_1 - 5n_0) = +0.0064 c/d and
n_2 - (n_1- 2/3 n_0) = -0.0065 c/d, with errors probably not exceeding
+- 0.0002 c/d, so that the detuning effect on the primary frequency n_1 is almost
exactly cancelled by the opposing actions of the two resonance terms.
In figures 4, 5 and 6 we illustrate the agreement between the adopted
radial velocity solution and the observations, and in figures 7, 8 and 9 the
same comparison is made for the light variation. For the velocities only on
the first night does the solution appear unsatisfactory, and it was just this
night that showed the large residual on the radial velocity curve. The representation
of the observed light variation appears generally satisfactory except for the
last night in the first (1950) observing season. But since the signalto-noise
ratio for this first season is much lower than in 1951 and 1952, it is not
certain that the discrepancies here are significant.
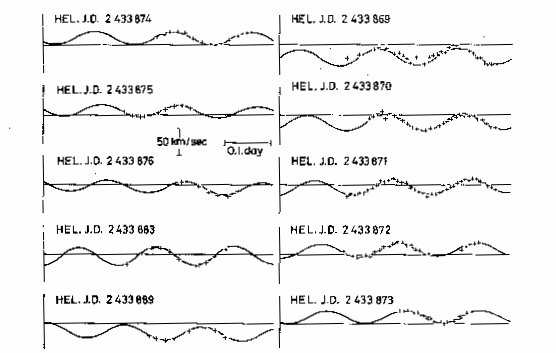 Fig. 4. A comparison of the observed (crosses) and computed (full curve) radial
velocity variation of 16 Lacertae.
Fig. 4. A comparison of the observed (crosses) and computed (full curve) radial
velocity variation of 16 Lacertae.
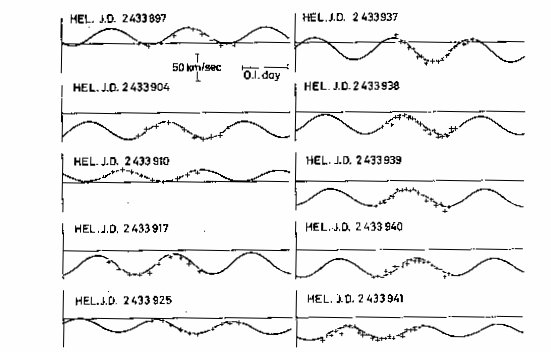 Fig. 5. Cont. of Fig. 4
Fig. 5. Cont. of Fig. 4
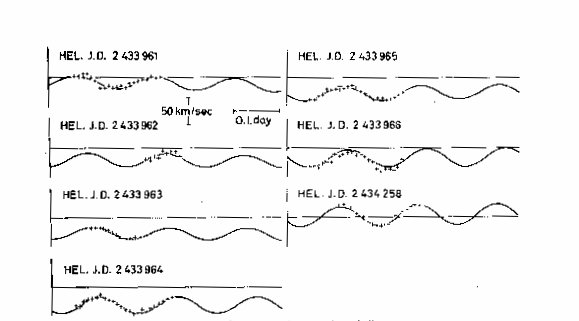 Fig. 6. Cont. of Figs. 4 and 5
Fig. 6. Cont. of Figs. 4 and 5
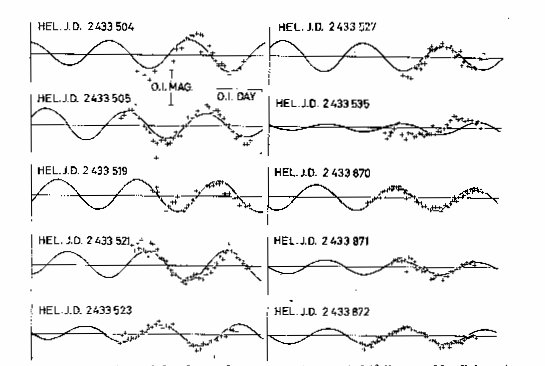 Fig. 7. A comparison of the observed (crosses) and computed (full curve)
blue lightvariation of 16 Lacertae.
Fig. 7. A comparison of the observed (crosses) and computed (full curve)
blue lightvariation of 16 Lacertae.
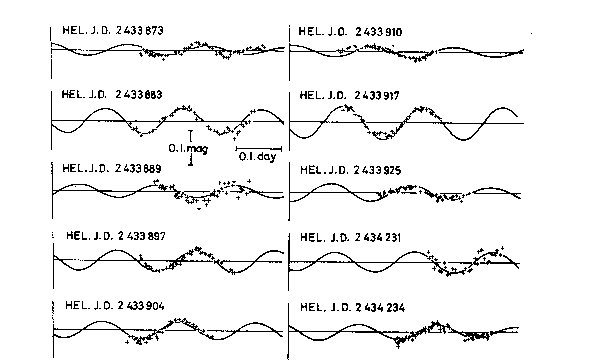 Fig. 8. Cont. of Fig. 7
Fig. 8. Cont. of Fig. 7
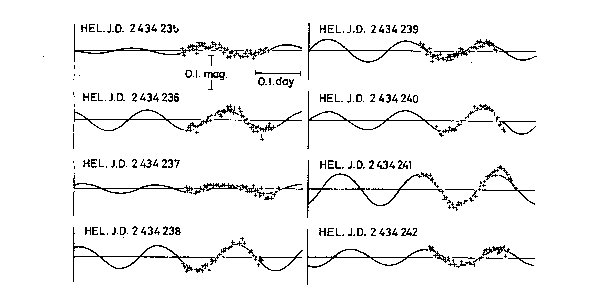 Fig. 9. Cont. of Figs. 7 and 8
It seems most likely that the beta Canis Majoris variation arises in rotating
stars caused to pulsate by a relatively short-lived instability associated with
core hydrogen exhaustion (Schmalberger 1960, Stothers 1965), and in order
to explain the spectral complexities observed during the pulsation cycle
(Huang and Struve 1955), it appears sufficient (Christy 1967) to identify the
primary pulsation with a P_2 non-radial mode (Ledoux 1951). Further, this
identification is consistent with theoretical expectation since in a star with
a significant rotation velocity a purely radial pulsation mode could probably
not exist (Chandrasekhar and Lebovitz 1962). In sigma Scorpii the modulation
of the primary pulsation has been shown to be associated with the orbital motion
in the binary system (van Hoof 1966, Fitch 1967), and the present results on
16 Lacertae indicate that here the n_2 and n_3 variations are non-radial modes
selectively excited by tidal resonances from the extremely numerous set of
possible rotational velocity dependent non-radial modes (Cowling and Newing 1949),
the rest of which are too highly damped to be significantly excited. We believe
that similar mechanisms of resonant and/or non-resonant tidal modulation
(cf. eqs. [1], [2], and [3]) exist in all other beta Canis Majoris and delta Scuti
stars that exhibit variable light or velocity curves (e.g. nu Andromedae,
sigma Scorpii, and CC Andromedae [Fitch 1967]), and we suggest the possibility
that the same cause also produces the long period modulation commonly observed
in RR Lyrae stars.
REFERENCES
Chandrasekhar, S., and Lebovitz, N. R., 1962, Astrophys. J., 136, 1105.
Christy, R. F., 1967, Astr. J., 72, 293.
Cowling, T. G. and Newing, R. A., 1949, Astrophys. J. 109, 149.
Fitch, W. S., 1967, Astrophys. J., 148, 481.
Hoof, A. van, 1966, Z. Astrophys., 64, 165.
Huang, S. S, and Struve, 0., 1955, Astrophys. J., 122, 103.
Ledoux, P., 1951, Astrophys. J., 114, 373.
Preston, G. W., 1966, Kleine Veröff. Remeis-Sternw. Bamberg, No. 40, p. 163.
Schmalberger, D. C., 1960, Astrophys. J., 132, 591.
Stothers, R., 1965, Astrophys. J., 141, 671.
Struve, O. and Bobrovnikoff, N. T., 1925, Astrophys. J., 62, 139.
Struve, 0., McNamara, D. H., Kraft, R. F., Kung, S. M, and Williams, A. D., 1952,
Astrophys. J., 116, 81.
Walker, M. F., 1951, Publ. astr. Soc. Pacific, 63, 35.
Walker, M. F., 1952, Astrophys. J., 116, 106.
Walker, M. F., 1953, Astrophys. J., 118, 481.
Walker, M. F., 1954, Astrophys. J., 120, 58.
Walker, M. F., 1967, (private communication).
Wehlau, W, and Leung, K. C., 1964, Astrophys. J., 139, 843.
DISCUSSION
Detre: Is the pulsation excited, or only influenced by the companion?
Fitch: No, the primary pulsation is not excited but only influenced by the
companion. It is caused by the evolution of the star carrying it into
either the beta Canis Majoris or Cepheid instability strip. However,
in 16 Lacertae it appears that two very weak pulsation modes which would
otherwise be changed out are excited by tidal resonances with the primary
pulsation.
Detre: Have beta CMa stars and delta Scuti stars erratic O-C diagrams, or smooth
ones? According to my opinion there may be some difference in the
behaviour of RR Lyrae variables and beta CMa stars, the former ones having
more erratic 0-C diagrams. Further, RR Lyrae stars with secondary
period have smaller amplitudes than RR Lyrae stars having stable lightcurve.
There is no such difference in the amplitudes of delta Sct stars and
dwarf Cepheids.
Fitch: As you have shown, the O-C diagrams of the RR Lyrae stars are quite
erratic, while so far as I am aware, the delta Scuti and beta Canis Majoris
stars have smooth O-C curves. However, this is not at all surprising, since
the beta Canis Majoris and delta Scuti stars are all very small amplitude
pulsators with behaviour probably governed by the linear wave equation
(they all have nearly sinusoidal, small amplitude variations), whereas
the RR Lyrae star pulsation is, as Christy has shown, governed by an
extremely non-linear set of equations. Therefore the amplitude, shape,
and frequency of an RR Lyrae star's pulsation must be very sensitively
determined by conditions in the outer layers of the star, and whenever
these layers are very slightly disturbed by evolutionary readjustment
(and perhaps also by the tides induced by a companion) the observed
pulsation characteristics must change - hence the erratic O-C behaviour
due to evolution and, perhaps, the long period modulation due to tides.
With regard to the dwarf Cepheid or AI Velorum stars, I know of none
that show long period modulation, though many have two pulsation
modes, simultaneously excited so that they show a very short period
beat. With regard to the small pulsation amplitude of RR Lyrae stars
having secondary periods, I think that probably when tides are present
the amplitude and phase of the normally radial pulsation vary in tidal
zones over the surface of the star, so that when the integrated light is
observed both light and velocity amplitudes will appear smaller than in
the normal case with no tides present.
Correction on March 7, 1969
I prepared for publication a paper which included an expanded version
of my Budapest lecture on 16 Lacertae, as well as an analysis of beta Cephei,
and then learned I'd overlooked some velocity measures of 16 Lacertae published
by Mc Namara. The addition of the new data and a more careful examination
of the errors involved has shown that only one of the two weak pulsation
modes has its apparently excitation due to tidal resonance, and that the other
is apparently excited by rotational coupling. This does not distress me, for
the original data used were consistent with my (erroneous) interpretation, and
the changes will be duly published.
However, in the course of this work I've re-calculated the orbital elements
with a new program we developed here, and found that there was an error in the
original program which we had copied from one then under development at
Kitt Peak National Observatory. I assume they now have a correct version, but
in the one we used a mistake had been made in programming the calculation of
phase from periastron for orbits of small eccentricity, with the result
that in my Figure 1 all phases are in error by 0.5 period.
Fig. 9. Cont. of Figs. 7 and 8
It seems most likely that the beta Canis Majoris variation arises in rotating
stars caused to pulsate by a relatively short-lived instability associated with
core hydrogen exhaustion (Schmalberger 1960, Stothers 1965), and in order
to explain the spectral complexities observed during the pulsation cycle
(Huang and Struve 1955), it appears sufficient (Christy 1967) to identify the
primary pulsation with a P_2 non-radial mode (Ledoux 1951). Further, this
identification is consistent with theoretical expectation since in a star with
a significant rotation velocity a purely radial pulsation mode could probably
not exist (Chandrasekhar and Lebovitz 1962). In sigma Scorpii the modulation
of the primary pulsation has been shown to be associated with the orbital motion
in the binary system (van Hoof 1966, Fitch 1967), and the present results on
16 Lacertae indicate that here the n_2 and n_3 variations are non-radial modes
selectively excited by tidal resonances from the extremely numerous set of
possible rotational velocity dependent non-radial modes (Cowling and Newing 1949),
the rest of which are too highly damped to be significantly excited. We believe
that similar mechanisms of resonant and/or non-resonant tidal modulation
(cf. eqs. [1], [2], and [3]) exist in all other beta Canis Majoris and delta Scuti
stars that exhibit variable light or velocity curves (e.g. nu Andromedae,
sigma Scorpii, and CC Andromedae [Fitch 1967]), and we suggest the possibility
that the same cause also produces the long period modulation commonly observed
in RR Lyrae stars.
REFERENCES
Chandrasekhar, S., and Lebovitz, N. R., 1962, Astrophys. J., 136, 1105.
Christy, R. F., 1967, Astr. J., 72, 293.
Cowling, T. G. and Newing, R. A., 1949, Astrophys. J. 109, 149.
Fitch, W. S., 1967, Astrophys. J., 148, 481.
Hoof, A. van, 1966, Z. Astrophys., 64, 165.
Huang, S. S, and Struve, 0., 1955, Astrophys. J., 122, 103.
Ledoux, P., 1951, Astrophys. J., 114, 373.
Preston, G. W., 1966, Kleine Veröff. Remeis-Sternw. Bamberg, No. 40, p. 163.
Schmalberger, D. C., 1960, Astrophys. J., 132, 591.
Stothers, R., 1965, Astrophys. J., 141, 671.
Struve, O. and Bobrovnikoff, N. T., 1925, Astrophys. J., 62, 139.
Struve, 0., McNamara, D. H., Kraft, R. F., Kung, S. M, and Williams, A. D., 1952,
Astrophys. J., 116, 81.
Walker, M. F., 1951, Publ. astr. Soc. Pacific, 63, 35.
Walker, M. F., 1952, Astrophys. J., 116, 106.
Walker, M. F., 1953, Astrophys. J., 118, 481.
Walker, M. F., 1954, Astrophys. J., 120, 58.
Walker, M. F., 1967, (private communication).
Wehlau, W, and Leung, K. C., 1964, Astrophys. J., 139, 843.
DISCUSSION
Detre: Is the pulsation excited, or only influenced by the companion?
Fitch: No, the primary pulsation is not excited but only influenced by the
companion. It is caused by the evolution of the star carrying it into
either the beta Canis Majoris or Cepheid instability strip. However,
in 16 Lacertae it appears that two very weak pulsation modes which would
otherwise be changed out are excited by tidal resonances with the primary
pulsation.
Detre: Have beta CMa stars and delta Scuti stars erratic O-C diagrams, or smooth
ones? According to my opinion there may be some difference in the
behaviour of RR Lyrae variables and beta CMa stars, the former ones having
more erratic 0-C diagrams. Further, RR Lyrae stars with secondary
period have smaller amplitudes than RR Lyrae stars having stable lightcurve.
There is no such difference in the amplitudes of delta Sct stars and
dwarf Cepheids.
Fitch: As you have shown, the O-C diagrams of the RR Lyrae stars are quite
erratic, while so far as I am aware, the delta Scuti and beta Canis Majoris
stars have smooth O-C curves. However, this is not at all surprising, since
the beta Canis Majoris and delta Scuti stars are all very small amplitude
pulsators with behaviour probably governed by the linear wave equation
(they all have nearly sinusoidal, small amplitude variations), whereas
the RR Lyrae star pulsation is, as Christy has shown, governed by an
extremely non-linear set of equations. Therefore the amplitude, shape,
and frequency of an RR Lyrae star's pulsation must be very sensitively
determined by conditions in the outer layers of the star, and whenever
these layers are very slightly disturbed by evolutionary readjustment
(and perhaps also by the tides induced by a companion) the observed
pulsation characteristics must change - hence the erratic O-C behaviour
due to evolution and, perhaps, the long period modulation due to tides.
With regard to the dwarf Cepheid or AI Velorum stars, I know of none
that show long period modulation, though many have two pulsation
modes, simultaneously excited so that they show a very short period
beat. With regard to the small pulsation amplitude of RR Lyrae stars
having secondary periods, I think that probably when tides are present
the amplitude and phase of the normally radial pulsation vary in tidal
zones over the surface of the star, so that when the integrated light is
observed both light and velocity amplitudes will appear smaller than in
the normal case with no tides present.
Correction on March 7, 1969
I prepared for publication a paper which included an expanded version
of my Budapest lecture on 16 Lacertae, as well as an analysis of beta Cephei,
and then learned I'd overlooked some velocity measures of 16 Lacertae published
by Mc Namara. The addition of the new data and a more careful examination
of the errors involved has shown that only one of the two weak pulsation
modes has its apparently excitation due to tidal resonance, and that the other
is apparently excited by rotational coupling. This does not distress me, for
the original data used were consistent with my (erroneous) interpretation, and
the changes will be duly published.
However, in the course of this work I've re-calculated the orbital elements
with a new program we developed here, and found that there was an error in the
original program which we had copied from one then under development at
Kitt Peak National Observatory. I assume they now have a correct version, but
in the one we used a mistake had been made in programming the calculation of
phase from periastron for orbits of small eccentricity, with the result
that in my Figure 1 all phases are in error by 0.5 period.
 Fig. 1. The orbital radial velocity variation of the primary component of 16 Lacertae.
The plotted points are mean velocity measures for individual nights and the full curve
is the computed solution.
The nightly luminosity means vary strongly in an apparently erratic
fashion which we were unable to correlate with the orbital motion, and since
the comparison star 14 Lacertae has been reported to be variable (Walker
1952, 1953), it was necessary to attribute these variations in the mean light
level to 14 Lacertae and to compensate for them by applying night corrections
deduced from the mean values of the luminosity ratio. This arbitrary correction
procedure automatically precludes the possibility of finding any light variation
which depends solely on the orbital motion.
When the velocity and light measures had been freed of the principal
slow variations by means of the known orbital motion (here represented as
a sinusoidal velocity variation with frequency n_0 = 0.08279 c/d) and the
night corrections, respectively, further periodogram analysis disclosed the
existence of two more periodic variations (frequencies n_2 = 5.8529 and n_3 =
= 5.4998 c/d, in addition to the primary frequency n_1 = 5.9113 c/d) in both
the light and velocity observations. The three photometric observing seasons
were from J.D. 2433504 to 2433536, 2433870 to 2433926, and 2434231 to
2434242, while we have divided the principal velocity observing season in
two halves running from 2433869 to 2433926 and 2433937 to 2433967. The
principal data relating to these variations is summarized in Tables 1 and 2,
in which it is seen that the velocity-to-light amplitude ratio is much larger
for n_1 than for n_2 and n_3 (about 6.0, 3.0, and 1.5 km/sec percent mean light,
respectively), and also that the amplitude of n_3 varies strongly and apparently
concordantly in both light and velocity measures. The former observation
is illustrated by Figures 2 and 3, which show from the results of fitting to
simultaneous light and velocity measures obtained on 11 nights that both
amplitude and phase perturbations of the primary pulsation are much stronger
in light than in velocity, while the latter conclusion suggests the possibility
of long period interference effects arising from a close frequency doublet.
Since the annual cycle count is uncertain due to the very short photometric
observing seasons, the pulsation frequencies derived by periodogram analysis
could be in error by one cycle per year = 0.0027 c/d, though they are otherwise
accurate to +-0.0002 c/d or better. A proper change of 0.0027 c/d in n_2 and
in n_3 would in each case produce a nearly perfect tidal resonance, so exact
resonances were assumed and subsequent periodogram analysis disclosed the
existence in the light and velocity variations of the corresponding doublet
components of frequencies n_2 and n_3, as shown in Table 3.
Table 1
Blue Light Variation of 16 Lacertae
Frequency Blue Light Range (%) Phase Zero Point (Periods) M. E.
Year 5.9113 5.8529 5.4998 5.9113 5.8529 5.4998 of 1 obs. No. of Obs.
1950 ........... 4.8 2.3 3.1 0.590 0.281 0.565 1.6 242
1951 ........... 4.6 2.4 0.3 0.617 0.242 0.567 0.7 473
1952 4.5 2.5 2.7 0.618 0.225 0.550 0.8 452
1950, 1952 4.5 2.5 2.7 0.611 0.231 0.560 1.1 694
1950, 51, 52 4.7 2.4 1.9 0.612 0.235 0.560 1.0 1167
Table 2
Velocity Variation of 16 Lacertae
Frequency Velocity Range (km/sec) Phase Zero Point (Periods) M. E.
Year 5.9113 5.8529 5.4998 5.9113 5.8529 5.4998 of 1 obs. No. of Obs.
1951-1st 1/2 27.5 6.8 0.8 0.857 0.503 0.895 3.5 234
1951-2nd 1/2 29.3 7.2 4.1 0.852 0.548 0.864 3.5 208
All 1951 28.3 6.9 2.2 0.854 0.516 0.876 3.6 442
1951, 1952 28.6 7.2 2.3 0.855 0.514 0.885 3.6 456
Fig. 1. The orbital radial velocity variation of the primary component of 16 Lacertae.
The plotted points are mean velocity measures for individual nights and the full curve
is the computed solution.
The nightly luminosity means vary strongly in an apparently erratic
fashion which we were unable to correlate with the orbital motion, and since
the comparison star 14 Lacertae has been reported to be variable (Walker
1952, 1953), it was necessary to attribute these variations in the mean light
level to 14 Lacertae and to compensate for them by applying night corrections
deduced from the mean values of the luminosity ratio. This arbitrary correction
procedure automatically precludes the possibility of finding any light variation
which depends solely on the orbital motion.
When the velocity and light measures had been freed of the principal
slow variations by means of the known orbital motion (here represented as
a sinusoidal velocity variation with frequency n_0 = 0.08279 c/d) and the
night corrections, respectively, further periodogram analysis disclosed the
existence of two more periodic variations (frequencies n_2 = 5.8529 and n_3 =
= 5.4998 c/d, in addition to the primary frequency n_1 = 5.9113 c/d) in both
the light and velocity observations. The three photometric observing seasons
were from J.D. 2433504 to 2433536, 2433870 to 2433926, and 2434231 to
2434242, while we have divided the principal velocity observing season in
two halves running from 2433869 to 2433926 and 2433937 to 2433967. The
principal data relating to these variations is summarized in Tables 1 and 2,
in which it is seen that the velocity-to-light amplitude ratio is much larger
for n_1 than for n_2 and n_3 (about 6.0, 3.0, and 1.5 km/sec percent mean light,
respectively), and also that the amplitude of n_3 varies strongly and apparently
concordantly in both light and velocity measures. The former observation
is illustrated by Figures 2 and 3, which show from the results of fitting to
simultaneous light and velocity measures obtained on 11 nights that both
amplitude and phase perturbations of the primary pulsation are much stronger
in light than in velocity, while the latter conclusion suggests the possibility
of long period interference effects arising from a close frequency doublet.
Since the annual cycle count is uncertain due to the very short photometric
observing seasons, the pulsation frequencies derived by periodogram analysis
could be in error by one cycle per year = 0.0027 c/d, though they are otherwise
accurate to +-0.0002 c/d or better. A proper change of 0.0027 c/d in n_2 and
in n_3 would in each case produce a nearly perfect tidal resonance, so exact
resonances were assumed and subsequent periodogram analysis disclosed the
existence in the light and velocity variations of the corresponding doublet
components of frequencies n_2 and n_3, as shown in Table 3.
Table 1
Blue Light Variation of 16 Lacertae
Frequency Blue Light Range (%) Phase Zero Point (Periods) M. E.
Year 5.9113 5.8529 5.4998 5.9113 5.8529 5.4998 of 1 obs. No. of Obs.
1950 ........... 4.8 2.3 3.1 0.590 0.281 0.565 1.6 242
1951 ........... 4.6 2.4 0.3 0.617 0.242 0.567 0.7 473
1952 4.5 2.5 2.7 0.618 0.225 0.550 0.8 452
1950, 1952 4.5 2.5 2.7 0.611 0.231 0.560 1.1 694
1950, 51, 52 4.7 2.4 1.9 0.612 0.235 0.560 1.0 1167
Table 2
Velocity Variation of 16 Lacertae
Frequency Velocity Range (km/sec) Phase Zero Point (Periods) M. E.
Year 5.9113 5.8529 5.4998 5.9113 5.8529 5.4998 of 1 obs. No. of Obs.
1951-1st 1/2 27.5 6.8 0.8 0.857 0.503 0.895 3.5 234
1951-2nd 1/2 29.3 7.2 4.1 0.852 0.548 0.864 3.5 208
All 1951 28.3 6.9 2.2 0.854 0.516 0.876 3.6 442
1951, 1952 28.6 7.2 2.3 0.855 0.514 0.885 3.6 456
 Fig. 2. A comparison of the variations
in radial velocity and blue light ranges
of the primary pulsation, as determined
by simultaneous observations on 11 nights.
Extrapolations of the straight lines bounding
the observed region do not enclose the origin.
Fig. 2. A comparison of the variations
in radial velocity and blue light ranges
of the primary pulsation, as determined
by simultaneous observations on 11 nights.
Extrapolations of the straight lines bounding
the observed region do not enclose the origin.
 Fig. 3. A comparison of the variations in radial
velocity and blue light of the primary pulsation's
phase zero point, as determined by simultaneous
observations on 11 nights. The straight line was
drawn with slope 1/2.
Table 3.
Adopted Solution for 16 Lacertae
Frequency Description Half Range Phase Zero Point
(c/d) (km/sec) (% light) R. V. Light
5.9177 n_3 + 5n_0 0.3 0.26 0.11 0.41
5.9113 n_1 14.4 2.41 0.85 0.63
5.9048 n_2 + 2/3n_0 0.8 0.24 0.06 0.89
5.8561 n_1 - 2/3n_0 2.9 0.70 0.56 0.42
5.8496 n_2 2.2 0.76 0.57 0.20
5.5037 n_3 1.0 0.82 0.23 0.79
5.4973 n_1 - 5n_0 0.9 0.83 0.16 0.60
0.08279 n_0 22.9 0.88
0.1656 2n_0 0.7 0.21
0.2484 3n_0 0.5 0.39
0.3312 4n_0 1.2 0.08
To explain this result, we consider a system of N coupled linear oscillators,
in which the state of the k^th oscillator (of natural frequency n_k) is specified
by the generalized coordinate q_k, and on which an external periodic force F
of frequency n_0 (where n_0 << n_k) acts. We assume we can expand each
component of F in a Fourier series harmonic in n_0, so that, neglecting both
the direct response of the system to the imposed force F and non-linear terms
in the coordinates q_k, we have
Fig. 3. A comparison of the variations in radial
velocity and blue light of the primary pulsation's
phase zero point, as determined by simultaneous
observations on 11 nights. The straight line was
drawn with slope 1/2.
Table 3.
Adopted Solution for 16 Lacertae
Frequency Description Half Range Phase Zero Point
(c/d) (km/sec) (% light) R. V. Light
5.9177 n_3 + 5n_0 0.3 0.26 0.11 0.41
5.9113 n_1 14.4 2.41 0.85 0.63
5.9048 n_2 + 2/3n_0 0.8 0.24 0.06 0.89
5.8561 n_1 - 2/3n_0 2.9 0.70 0.56 0.42
5.8496 n_2 2.2 0.76 0.57 0.20
5.5037 n_3 1.0 0.82 0.23 0.79
5.4973 n_1 - 5n_0 0.9 0.83 0.16 0.60
0.08279 n_0 22.9 0.88
0.1656 2n_0 0.7 0.21
0.2484 3n_0 0.5 0.39
0.3312 4n_0 1.2 0.08
To explain this result, we consider a system of N coupled linear oscillators,
in which the state of the k^th oscillator (of natural frequency n_k) is specified
by the generalized coordinate q_k, and on which an external periodic force F
of frequency n_0 (where n_0 << n_k) acts. We assume we can expand each
component of F in a Fourier series harmonic in n_0, so that, neglecting both
the direct response of the system to the imposed force F and non-linear terms
in the coordinates q_k, we have
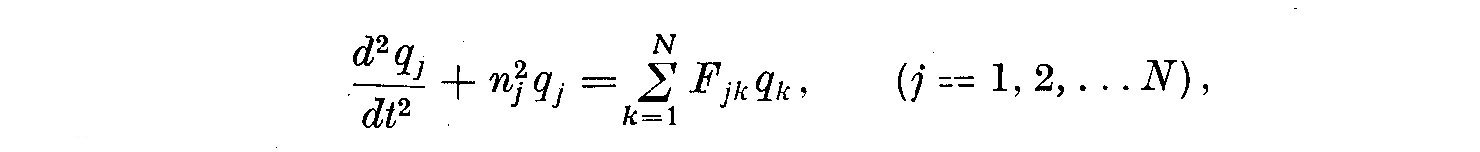 (1)
where
(1)
where
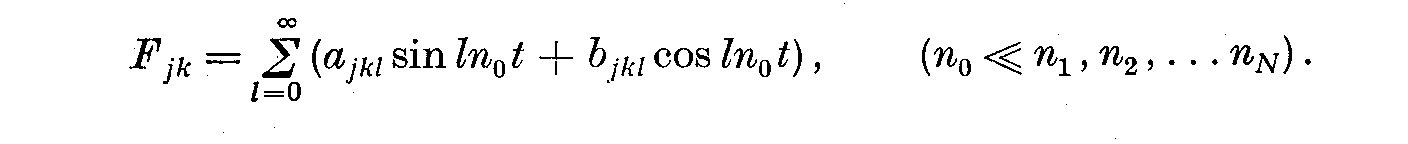 (2)
It is easily shown that the periodic solutions of these equations, complete to
the second order, may be written in the form
(2)
It is easily shown that the periodic solutions of these equations, complete to
the second order, may be written in the form
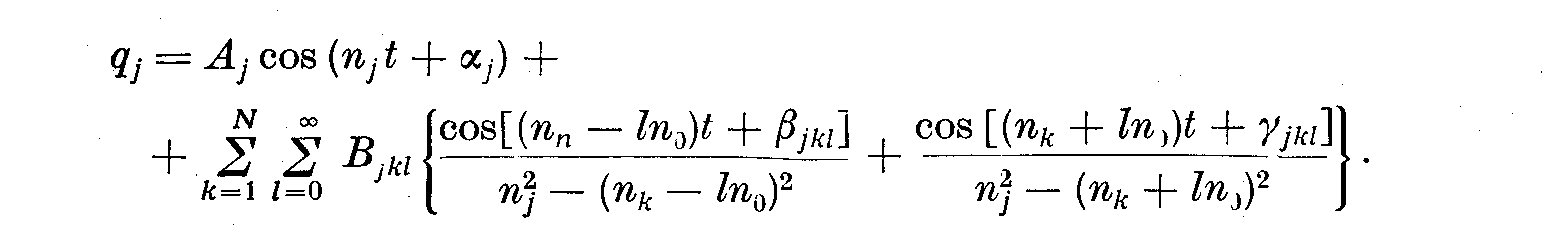 (3)
Thus the solution will contain both the natural frequencies n_k and also the
combination terms n_k +- ln_0 but of the latter the most important are likely
to be those (if any) for which a near resonance exists (i.e. [n_k +- ln_0]^2 ~~n^2_j).
Of course, terms with the forcing frequencies ln_0 which were neglected in
equations (1), will also exist. Our foregoing argument for the resonance case
requires, strictly speaking, that l be integer, but as is well known, resonance
often occurs when l is rational, provided it is the quotient of two small integers
(e.g. the Kirkwood gaps and the Hilda group in the case of the asteroids). In
the present case, with P_0 as the orbital period in a nearly (or perhaps exactly)
circular orbit, the tidal perturbations are nearly the same at intervals of
1/2 P_0, P_0 and 3/2 P_0, so that the strongest perturbing frequencies should be
2n_0, n_0, and 2/3 n_0.
Since the two resonance pairs of difference frequencies (n_2, n_1 - 2/3 n_0)
and (n_3, n_1 - 5n_0) had been observed, in accordance with the preceding analysis
the corresponding sum frequencies n_2 + 2/3 n_0 and n_3 + 5 n_0 were included
in the least squares fitting for the adopted solution displayed in Table 3.
That these sum terms are of very small amplitude (and perhaps not present)
is not surprising, since they arise from tidal action on the very weak terms
n_2 and n_3, whereas the difference terms here originate in the action of F on n_1.
The ordinary, non-resonant combination terms n_1 +- ln_0, were also included
in a fitting with l = 1, 2, and 3, and are probably present but are of too small
amplitude to be significant. We note that n_3 - (n_1 - 5n_0) = +0.0064 c/d and
n_2 - (n_1- 2/3 n_0) = -0.0065 c/d, with errors probably not exceeding
+- 0.0002 c/d, so that the detuning effect on the primary frequency n_1 is almost
exactly cancelled by the opposing actions of the two resonance terms.
In figures 4, 5 and 6 we illustrate the agreement between the adopted
radial velocity solution and the observations, and in figures 7, 8 and 9 the
same comparison is made for the light variation. For the velocities only on
the first night does the solution appear unsatisfactory, and it was just this
night that showed the large residual on the radial velocity curve. The representation
of the observed light variation appears generally satisfactory except for the
last night in the first (1950) observing season. But since the signalto-noise
ratio for this first season is much lower than in 1951 and 1952, it is not
certain that the discrepancies here are significant.
(3)
Thus the solution will contain both the natural frequencies n_k and also the
combination terms n_k +- ln_0 but of the latter the most important are likely
to be those (if any) for which a near resonance exists (i.e. [n_k +- ln_0]^2 ~~n^2_j).
Of course, terms with the forcing frequencies ln_0 which were neglected in
equations (1), will also exist. Our foregoing argument for the resonance case
requires, strictly speaking, that l be integer, but as is well known, resonance
often occurs when l is rational, provided it is the quotient of two small integers
(e.g. the Kirkwood gaps and the Hilda group in the case of the asteroids). In
the present case, with P_0 as the orbital period in a nearly (or perhaps exactly)
circular orbit, the tidal perturbations are nearly the same at intervals of
1/2 P_0, P_0 and 3/2 P_0, so that the strongest perturbing frequencies should be
2n_0, n_0, and 2/3 n_0.
Since the two resonance pairs of difference frequencies (n_2, n_1 - 2/3 n_0)
and (n_3, n_1 - 5n_0) had been observed, in accordance with the preceding analysis
the corresponding sum frequencies n_2 + 2/3 n_0 and n_3 + 5 n_0 were included
in the least squares fitting for the adopted solution displayed in Table 3.
That these sum terms are of very small amplitude (and perhaps not present)
is not surprising, since they arise from tidal action on the very weak terms
n_2 and n_3, whereas the difference terms here originate in the action of F on n_1.
The ordinary, non-resonant combination terms n_1 +- ln_0, were also included
in a fitting with l = 1, 2, and 3, and are probably present but are of too small
amplitude to be significant. We note that n_3 - (n_1 - 5n_0) = +0.0064 c/d and
n_2 - (n_1- 2/3 n_0) = -0.0065 c/d, with errors probably not exceeding
+- 0.0002 c/d, so that the detuning effect on the primary frequency n_1 is almost
exactly cancelled by the opposing actions of the two resonance terms.
In figures 4, 5 and 6 we illustrate the agreement between the adopted
radial velocity solution and the observations, and in figures 7, 8 and 9 the
same comparison is made for the light variation. For the velocities only on
the first night does the solution appear unsatisfactory, and it was just this
night that showed the large residual on the radial velocity curve. The representation
of the observed light variation appears generally satisfactory except for the
last night in the first (1950) observing season. But since the signalto-noise
ratio for this first season is much lower than in 1951 and 1952, it is not
certain that the discrepancies here are significant.
 Fig. 4. A comparison of the observed (crosses) and computed (full curve) radial
velocity variation of 16 Lacertae.
Fig. 4. A comparison of the observed (crosses) and computed (full curve) radial
velocity variation of 16 Lacertae.
 Fig. 5. Cont. of Fig. 4
Fig. 5. Cont. of Fig. 4
 Fig. 6. Cont. of Figs. 4 and 5
Fig. 6. Cont. of Figs. 4 and 5
 Fig. 7. A comparison of the observed (crosses) and computed (full curve)
blue lightvariation of 16 Lacertae.
Fig. 7. A comparison of the observed (crosses) and computed (full curve)
blue lightvariation of 16 Lacertae.
 Fig. 8. Cont. of Fig. 7
Fig. 8. Cont. of Fig. 7
 Fig. 9. Cont. of Figs. 7 and 8
It seems most likely that the beta Canis Majoris variation arises in rotating
stars caused to pulsate by a relatively short-lived instability associated with
core hydrogen exhaustion (Schmalberger 1960, Stothers 1965), and in order
to explain the spectral complexities observed during the pulsation cycle
(Huang and Struve 1955), it appears sufficient (Christy 1967) to identify the
primary pulsation with a P_2 non-radial mode (Ledoux 1951). Further, this
identification is consistent with theoretical expectation since in a star with
a significant rotation velocity a purely radial pulsation mode could probably
not exist (Chandrasekhar and Lebovitz 1962). In sigma Scorpii the modulation
of the primary pulsation has been shown to be associated with the orbital motion
in the binary system (van Hoof 1966, Fitch 1967), and the present results on
16 Lacertae indicate that here the n_2 and n_3 variations are non-radial modes
selectively excited by tidal resonances from the extremely numerous set of
possible rotational velocity dependent non-radial modes (Cowling and Newing 1949),
the rest of which are too highly damped to be significantly excited. We believe
that similar mechanisms of resonant and/or non-resonant tidal modulation
(cf. eqs. [1], [2], and [3]) exist in all other beta Canis Majoris and delta Scuti
stars that exhibit variable light or velocity curves (e.g. nu Andromedae,
sigma Scorpii, and CC Andromedae [Fitch 1967]), and we suggest the possibility
that the same cause also produces the long period modulation commonly observed
in RR Lyrae stars.
REFERENCES
Chandrasekhar, S., and Lebovitz, N. R., 1962, Astrophys. J., 136, 1105.
Christy, R. F., 1967, Astr. J., 72, 293.
Cowling, T. G. and Newing, R. A., 1949, Astrophys. J. 109, 149.
Fitch, W. S., 1967, Astrophys. J., 148, 481.
Hoof, A. van, 1966, Z. Astrophys., 64, 165.
Huang, S. S, and Struve, 0., 1955, Astrophys. J., 122, 103.
Ledoux, P., 1951, Astrophys. J., 114, 373.
Preston, G. W., 1966, Kleine Veröff. Remeis-Sternw. Bamberg, No. 40, p. 163.
Schmalberger, D. C., 1960, Astrophys. J., 132, 591.
Stothers, R., 1965, Astrophys. J., 141, 671.
Struve, O. and Bobrovnikoff, N. T., 1925, Astrophys. J., 62, 139.
Struve, 0., McNamara, D. H., Kraft, R. F., Kung, S. M, and Williams, A. D., 1952,
Astrophys. J., 116, 81.
Walker, M. F., 1951, Publ. astr. Soc. Pacific, 63, 35.
Walker, M. F., 1952, Astrophys. J., 116, 106.
Walker, M. F., 1953, Astrophys. J., 118, 481.
Walker, M. F., 1954, Astrophys. J., 120, 58.
Walker, M. F., 1967, (private communication).
Wehlau, W, and Leung, K. C., 1964, Astrophys. J., 139, 843.
DISCUSSION
Detre: Is the pulsation excited, or only influenced by the companion?
Fitch: No, the primary pulsation is not excited but only influenced by the
companion. It is caused by the evolution of the star carrying it into
either the beta Canis Majoris or Cepheid instability strip. However,
in 16 Lacertae it appears that two very weak pulsation modes which would
otherwise be changed out are excited by tidal resonances with the primary
pulsation.
Detre: Have beta CMa stars and delta Scuti stars erratic O-C diagrams, or smooth
ones? According to my opinion there may be some difference in the
behaviour of RR Lyrae variables and beta CMa stars, the former ones having
more erratic 0-C diagrams. Further, RR Lyrae stars with secondary
period have smaller amplitudes than RR Lyrae stars having stable lightcurve.
There is no such difference in the amplitudes of delta Sct stars and
dwarf Cepheids.
Fitch: As you have shown, the O-C diagrams of the RR Lyrae stars are quite
erratic, while so far as I am aware, the delta Scuti and beta Canis Majoris
stars have smooth O-C curves. However, this is not at all surprising, since
the beta Canis Majoris and delta Scuti stars are all very small amplitude
pulsators with behaviour probably governed by the linear wave equation
(they all have nearly sinusoidal, small amplitude variations), whereas
the RR Lyrae star pulsation is, as Christy has shown, governed by an
extremely non-linear set of equations. Therefore the amplitude, shape,
and frequency of an RR Lyrae star's pulsation must be very sensitively
determined by conditions in the outer layers of the star, and whenever
these layers are very slightly disturbed by evolutionary readjustment
(and perhaps also by the tides induced by a companion) the observed
pulsation characteristics must change - hence the erratic O-C behaviour
due to evolution and, perhaps, the long period modulation due to tides.
With regard to the dwarf Cepheid or AI Velorum stars, I know of none
that show long period modulation, though many have two pulsation
modes, simultaneously excited so that they show a very short period
beat. With regard to the small pulsation amplitude of RR Lyrae stars
having secondary periods, I think that probably when tides are present
the amplitude and phase of the normally radial pulsation vary in tidal
zones over the surface of the star, so that when the integrated light is
observed both light and velocity amplitudes will appear smaller than in
the normal case with no tides present.
Correction on March 7, 1969
I prepared for publication a paper which included an expanded version
of my Budapest lecture on 16 Lacertae, as well as an analysis of beta Cephei,
and then learned I'd overlooked some velocity measures of 16 Lacertae published
by Mc Namara. The addition of the new data and a more careful examination
of the errors involved has shown that only one of the two weak pulsation
modes has its apparently excitation due to tidal resonance, and that the other
is apparently excited by rotational coupling. This does not distress me, for
the original data used were consistent with my (erroneous) interpretation, and
the changes will be duly published.
However, in the course of this work I've re-calculated the orbital elements
with a new program we developed here, and found that there was an error in the
original program which we had copied from one then under development at
Kitt Peak National Observatory. I assume they now have a correct version, but
in the one we used a mistake had been made in programming the calculation of
phase from periastron for orbits of small eccentricity, with the result
that in my Figure 1 all phases are in error by 0.5 period.
Fig. 9. Cont. of Figs. 7 and 8
It seems most likely that the beta Canis Majoris variation arises in rotating
stars caused to pulsate by a relatively short-lived instability associated with
core hydrogen exhaustion (Schmalberger 1960, Stothers 1965), and in order
to explain the spectral complexities observed during the pulsation cycle
(Huang and Struve 1955), it appears sufficient (Christy 1967) to identify the
primary pulsation with a P_2 non-radial mode (Ledoux 1951). Further, this
identification is consistent with theoretical expectation since in a star with
a significant rotation velocity a purely radial pulsation mode could probably
not exist (Chandrasekhar and Lebovitz 1962). In sigma Scorpii the modulation
of the primary pulsation has been shown to be associated with the orbital motion
in the binary system (van Hoof 1966, Fitch 1967), and the present results on
16 Lacertae indicate that here the n_2 and n_3 variations are non-radial modes
selectively excited by tidal resonances from the extremely numerous set of
possible rotational velocity dependent non-radial modes (Cowling and Newing 1949),
the rest of which are too highly damped to be significantly excited. We believe
that similar mechanisms of resonant and/or non-resonant tidal modulation
(cf. eqs. [1], [2], and [3]) exist in all other beta Canis Majoris and delta Scuti
stars that exhibit variable light or velocity curves (e.g. nu Andromedae,
sigma Scorpii, and CC Andromedae [Fitch 1967]), and we suggest the possibility
that the same cause also produces the long period modulation commonly observed
in RR Lyrae stars.
REFERENCES
Chandrasekhar, S., and Lebovitz, N. R., 1962, Astrophys. J., 136, 1105.
Christy, R. F., 1967, Astr. J., 72, 293.
Cowling, T. G. and Newing, R. A., 1949, Astrophys. J. 109, 149.
Fitch, W. S., 1967, Astrophys. J., 148, 481.
Hoof, A. van, 1966, Z. Astrophys., 64, 165.
Huang, S. S, and Struve, 0., 1955, Astrophys. J., 122, 103.
Ledoux, P., 1951, Astrophys. J., 114, 373.
Preston, G. W., 1966, Kleine Veröff. Remeis-Sternw. Bamberg, No. 40, p. 163.
Schmalberger, D. C., 1960, Astrophys. J., 132, 591.
Stothers, R., 1965, Astrophys. J., 141, 671.
Struve, O. and Bobrovnikoff, N. T., 1925, Astrophys. J., 62, 139.
Struve, 0., McNamara, D. H., Kraft, R. F., Kung, S. M, and Williams, A. D., 1952,
Astrophys. J., 116, 81.
Walker, M. F., 1951, Publ. astr. Soc. Pacific, 63, 35.
Walker, M. F., 1952, Astrophys. J., 116, 106.
Walker, M. F., 1953, Astrophys. J., 118, 481.
Walker, M. F., 1954, Astrophys. J., 120, 58.
Walker, M. F., 1967, (private communication).
Wehlau, W, and Leung, K. C., 1964, Astrophys. J., 139, 843.
DISCUSSION
Detre: Is the pulsation excited, or only influenced by the companion?
Fitch: No, the primary pulsation is not excited but only influenced by the
companion. It is caused by the evolution of the star carrying it into
either the beta Canis Majoris or Cepheid instability strip. However,
in 16 Lacertae it appears that two very weak pulsation modes which would
otherwise be changed out are excited by tidal resonances with the primary
pulsation.
Detre: Have beta CMa stars and delta Scuti stars erratic O-C diagrams, or smooth
ones? According to my opinion there may be some difference in the
behaviour of RR Lyrae variables and beta CMa stars, the former ones having
more erratic 0-C diagrams. Further, RR Lyrae stars with secondary
period have smaller amplitudes than RR Lyrae stars having stable lightcurve.
There is no such difference in the amplitudes of delta Sct stars and
dwarf Cepheids.
Fitch: As you have shown, the O-C diagrams of the RR Lyrae stars are quite
erratic, while so far as I am aware, the delta Scuti and beta Canis Majoris
stars have smooth O-C curves. However, this is not at all surprising, since
the beta Canis Majoris and delta Scuti stars are all very small amplitude
pulsators with behaviour probably governed by the linear wave equation
(they all have nearly sinusoidal, small amplitude variations), whereas
the RR Lyrae star pulsation is, as Christy has shown, governed by an
extremely non-linear set of equations. Therefore the amplitude, shape,
and frequency of an RR Lyrae star's pulsation must be very sensitively
determined by conditions in the outer layers of the star, and whenever
these layers are very slightly disturbed by evolutionary readjustment
(and perhaps also by the tides induced by a companion) the observed
pulsation characteristics must change - hence the erratic O-C behaviour
due to evolution and, perhaps, the long period modulation due to tides.
With regard to the dwarf Cepheid or AI Velorum stars, I know of none
that show long period modulation, though many have two pulsation
modes, simultaneously excited so that they show a very short period
beat. With regard to the small pulsation amplitude of RR Lyrae stars
having secondary periods, I think that probably when tides are present
the amplitude and phase of the normally radial pulsation vary in tidal
zones over the surface of the star, so that when the integrated light is
observed both light and velocity amplitudes will appear smaller than in
the normal case with no tides present.
Correction on March 7, 1969
I prepared for publication a paper which included an expanded version
of my Budapest lecture on 16 Lacertae, as well as an analysis of beta Cephei,
and then learned I'd overlooked some velocity measures of 16 Lacertae published
by Mc Namara. The addition of the new data and a more careful examination
of the errors involved has shown that only one of the two weak pulsation
modes has its apparently excitation due to tidal resonance, and that the other
is apparently excited by rotational coupling. This does not distress me, for
the original data used were consistent with my (erroneous) interpretation, and
the changes will be duly published.
However, in the course of this work I've re-calculated the orbital elements
with a new program we developed here, and found that there was an error in the
original program which we had copied from one then under development at
Kitt Peak National Observatory. I assume they now have a correct version, but
in the one we used a mistake had been made in programming the calculation of
phase from periastron for orbits of small eccentricity, with the result
that in my Figure 1 all phases are in error by 0.5 period.