Non-Periodic Phenomena in Variable Stars
IAU Colloquium, Budapest, 1968
PHOTOMETRIC EFFECTS FOR HIGHLY DISTORTED WHITE DWARF
SECONDARIES IN CLOSE BINARY SYSTEMS
S. M. RUCINSKI
Astronomical Observatory, University of Warsaw, Warsaw, Poland
As a by-product of an analysis of the light curves of the early-type
close binary systems (Rucinski 1969a), similar computations for the
highly distorted white dwarf hypothetical secondaries of certain
peculiar systems were made. The computations were carried out
numerically by integrating the monochromatic fluxes emerging from the
atmosphere over the visible surface of the star. The effects of eclipses
were not taken into account; the reflection effect was also excluded at
this step of analysis. A slightly different model atmosphere was used at
each point of the star's surface depending on the local effective
temperature (with the assumption of von Zeipel proportionality T_e ~ g^1/4).
The shape, variations of the effective gravity g, and the
cosine of the angle between the local normal to the surface and the
direction to the observer, mu, were described using the first order
perturbation theory for close binary systems (Chandrasekhar 1933). In
that theory the Legendre polynomial P_2 gives the ellipticity of the
star; the next P_3 and P_4 polynomials describe respectively the
non-symmetric and symmetric deviations from ellipticity.
By integrating over the visible surface S of the star we obtain a quantity
proportional to the total monochromatic energy radiated by the star in a
given direction:
L_nu= integral from S integral I_nu(mu,T_e)*mu*dS. (1)
The product L_nuA^2, where A is the separation of the binary components,
is the total energy radiated by the star in the observer's direction per
unit of frequency and per unit of time. L_nu evaluated as a function of
the phase angle describes the light changes caused by the distortion of
the star. More detailed description of the methods of computation will
be published elsewhere.
The emerging intensities I_nu at lambda = 5000 A were computed on the
basis of the white dwarf model atmospheres (Terashita, Matsushima 1966)
for the effective temperatures 8000deg and 10700deg and for the gravity
g = 10^7. These intensities were represented by the series:
I_nu (mu, T_e) = Summa from n=0 to 3 I_nu n(T_e)*mu^n. (2)
As the mean effective temperature of the white dwarf secondary was taken near
7800deg in computing the integral (1) the values of I_nu (mu, T_e) in
particular points of the star's surface were found either by interpolation or
by extrapolation of both the model atmospheres depending whether the effective
temperature was in or out of the range 8000deg -10700deg.
The following assumptions were made: the inclination of the orbit
i = 90deg, the synchronism of the star's rotation and the orbital revolution,
and the Roche model for the concentration of mass towards the centre.
Two cases were computed with two different mass ratios. In each case the
dimensions of the stars were chosen in such way as to fit the corresponding
Roche lobe (Plavec, Krotochvil 1964; Kuiper, Johnson 1956) in the direction
of the y-axis which lies in the orbital plane and is perpendicular to the
x-axis joining the centres of the stars. The mass ratios and the respective
dimensions (in units of the separation of the components, A) are:
Case M_pri/M_WD x_a x_b y z
1 10 .226 .219 .197 .187
2 19 .187 .182 .162 .154
Because of the simplified description of the stars the conical parts directed
towards the Lagrangian L_1 point are obviously not filled, but elsewhere the
approximation of the Roche lobes is relatively good (Fig. 1); in any case we
might expect that the photometric effects caused by the distortion of the star
will be rather under-estimated than over-estimated in this way. The changes
in L_nu are given by the formula:
L_nu = C_0 * (1 + Summa from n=1 to 3 C_n * cos (n * Phase)) (3)
where the Fourier coefficients C_n for the computed cases (the accuracy
being approximately 0.0005) are:
Case C_0 C_1 C_2 C_3
1 7.62X10^-6 -0.0132 -0.2278 -0.0112
2 5.16x10^-6 -0.0122 -0.2467 -0.0099
In both cases the full amplitude of the light variations amounts to almost
three quarters of a magnitude. This implies, therefore, that a strongly
distorted white dwarf secondary whose contribution to the total brightness
of the system may be quite low, might easily account for the quasi-sinusoidal
variations observed in such systems as WZ Sge (Krzeminski, Kraft 1964) and,
perhaps, BD +14deg 341 (Smak, Stepien 1968).
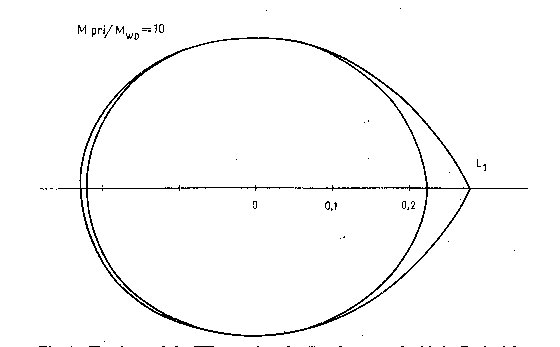 Fig. 1a. The shape of the WD secondary for Case 1 compared with its Roche lobe
(orbital plane section).
Fig. 1a. The shape of the WD secondary for Case 1 compared with its Roche lobe
(orbital plane section).
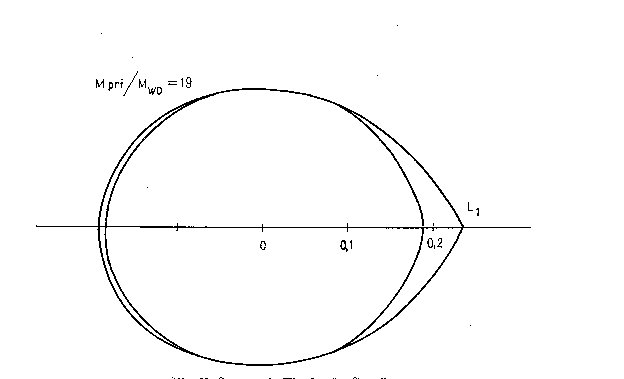 Fig. 1b. Same as in Fig. 1a. for Case 2.
There is no theory which could be used to evaluate the expected values of
the coefficients C_1 and C_3, both the coefficients giving the asymmetry of the
light curve. The largest coefficient C_2, however, can be estimated on the
basis of the geometric parameters of the star and the limb (u) and gravity (y)
darkening coefficients determined from the same previously used model
atmospheres. The theoretical value of C_2 will be:
C'_2 = 15+u/10*(3-u)*(1+y)*epsilon,
where epsilon describes the shape of the star under the assumption of its
pure ellipticity. epsilon might be approximated by (Russell, Merrill 1952):
a) epsilon = (a - b)/a, where a and b are the two axes of the ellipsoid
lying in the orbital plane,
b) epsilon = 3/2 * (M_pri/M_WD) * (r/A)^3, where r is the mean radius of
the star, equal to the radius of a sphere of the same volume.
Comparing C'_2 computed in this way (for T_e = 7800deg, u = 0.627, and y =
= 0.785) with C_2 obtained previously, we have the following ratios C_2/C'_2:
a) b)
Case 1 1.70 1.60
Case 2 1.74 1.62
The simpler theory leads therefore to the value of C_2 which is 60-70 per cent
smaller than that obtained from the model described above.
As a check a modification of Case 1 was computed by assuming T_e = constant
over the whole surface of the star; that is, only the geometrical and limb
darkening effects were taken into account. The ratio C_2/C'_2 was then:
a) b)
C_2/C'_2 1.05 0.98
in general agreement with the rather approximate theory.
As we see the main effect increasing the observable amplitude of the
light variations is the strong dependence of the emerging intensity on
the gravitation via the effective temperature; this dependence cannot be
fully described by a simple gravity darkening coefficient. The dependence
also manifests itself in the distribution of the emerging intensity over
the star's disc and spots of different brightness are formed on it. The shape,
dimensions and intensity of these spots depend strongly on the orientation
relative to the observer (Fig. 2 and the following) and in the case of an
eclipsing system they might complicate very much the interpretation of the
light variations resulting from the eclipses.
More detailed description of the results presented here will be given
elsewhere (Rucinski 1969b).
The author is indebted to Dr. J. Smak for arousing his interest in the
subject.
Fig. 1b. Same as in Fig. 1a. for Case 2.
There is no theory which could be used to evaluate the expected values of
the coefficients C_1 and C_3, both the coefficients giving the asymmetry of the
light curve. The largest coefficient C_2, however, can be estimated on the
basis of the geometric parameters of the star and the limb (u) and gravity (y)
darkening coefficients determined from the same previously used model
atmospheres. The theoretical value of C_2 will be:
C'_2 = 15+u/10*(3-u)*(1+y)*epsilon,
where epsilon describes the shape of the star under the assumption of its
pure ellipticity. epsilon might be approximated by (Russell, Merrill 1952):
a) epsilon = (a - b)/a, where a and b are the two axes of the ellipsoid
lying in the orbital plane,
b) epsilon = 3/2 * (M_pri/M_WD) * (r/A)^3, where r is the mean radius of
the star, equal to the radius of a sphere of the same volume.
Comparing C'_2 computed in this way (for T_e = 7800deg, u = 0.627, and y =
= 0.785) with C_2 obtained previously, we have the following ratios C_2/C'_2:
a) b)
Case 1 1.70 1.60
Case 2 1.74 1.62
The simpler theory leads therefore to the value of C_2 which is 60-70 per cent
smaller than that obtained from the model described above.
As a check a modification of Case 1 was computed by assuming T_e = constant
over the whole surface of the star; that is, only the geometrical and limb
darkening effects were taken into account. The ratio C_2/C'_2 was then:
a) b)
C_2/C'_2 1.05 0.98
in general agreement with the rather approximate theory.
As we see the main effect increasing the observable amplitude of the
light variations is the strong dependence of the emerging intensity on
the gravitation via the effective temperature; this dependence cannot be
fully described by a simple gravity darkening coefficient. The dependence
also manifests itself in the distribution of the emerging intensity over
the star's disc and spots of different brightness are formed on it. The shape,
dimensions and intensity of these spots depend strongly on the orientation
relative to the observer (Fig. 2 and the following) and in the case of an
eclipsing system they might complicate very much the interpretation of the
light variations resulting from the eclipses.
More detailed description of the results presented here will be given
elsewhere (Rucinski 1969b).
The author is indebted to Dr. J. Smak for arousing his interest in the
subject.
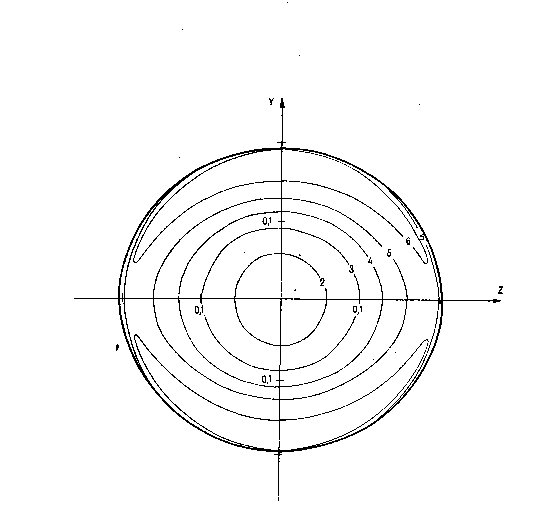 Fig. 2. The distribution of the emerging intensity over the visible disc
of the WD secondary. The mass ratio is 10 (Case 1). The isophotes are labelled
with numbers which should be multiplied by 10^-5 to give the intensity I_nu
in cgs units. The X-axis is directed towards the observer and the rotation
axis lies in the XZ-plane. The inclination of the orbit is i = 90deg;
the phase phi = 0deg, i.e, the star is viewed from the primary
component.
Fig. 2. The distribution of the emerging intensity over the visible disc
of the WD secondary. The mass ratio is 10 (Case 1). The isophotes are labelled
with numbers which should be multiplied by 10^-5 to give the intensity I_nu
in cgs units. The X-axis is directed towards the observer and the rotation
axis lies in the XZ-plane. The inclination of the orbit is i = 90deg;
the phase phi = 0deg, i.e, the star is viewed from the primary
component.
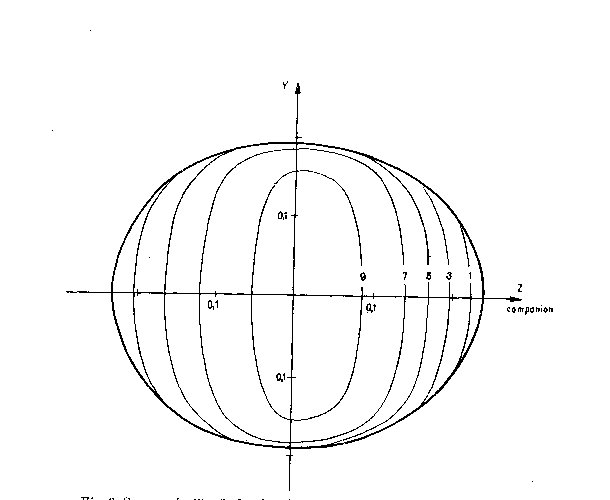 Fig. 3. Same as in Fig. 2, for the phase phi = 90deg, i.e. the star is
viewed side-on.
Fig. 3. Same as in Fig. 2, for the phase phi = 90deg, i.e. the star is
viewed side-on.
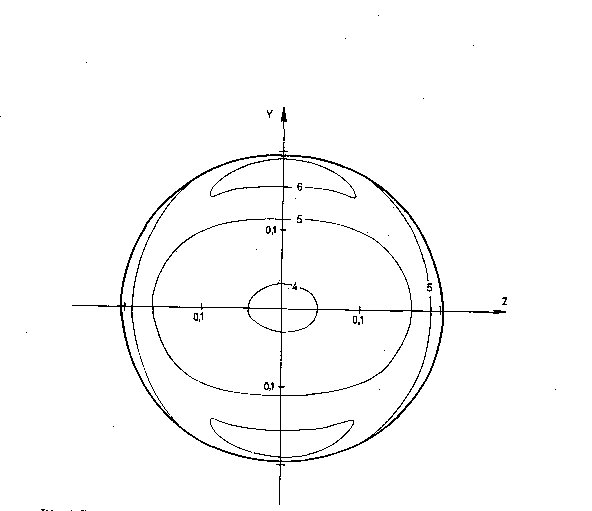 Fig. 4. Same as in Fig. 2, for the phase phi = 180deg, i.e. the opposite
side of the star is viewed.
Fig. 4. Same as in Fig. 2, for the phase phi = 180deg, i.e. the opposite
side of the star is viewed.
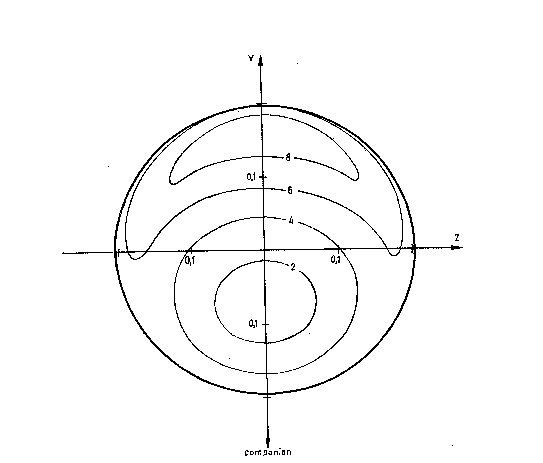 Fig. 5. Same as in Fig. 2, for the phase phi = 0deg but for the inclination
i = 75deg.
Fig. 5. Same as in Fig. 2, for the phase phi = 0deg but for the inclination
i = 75deg.
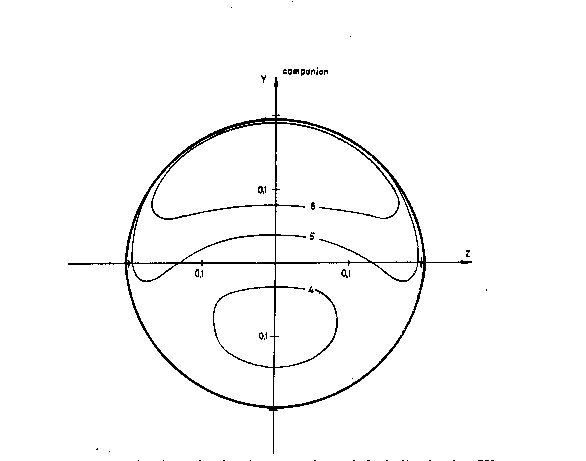 Fig. 6. Same as in Fig. 2, for the phase phi = 180deg and the
inclination i = 75deg.
REFERENCES
Chandrasekhar, S., 1933, Mon. Not. R. astr. Soc. 93, 462 and 539.
Krzeminski, W., Kraft, R. P., 1964, Astrophys. J. 140, 921.
Kuiper, G. P., Johnson, J. R., 1956, Astrophys. J. 123, 90.
Plavec, M., Krotochvil, P., 1964, Bull. astr. Inst. Csl. 5, 165.
Rucinski, S. M., 1969a, Acta Astr. in preparation.
Rucinski, S. M., 1969b, Acta Astr. in preparation.
Russell, H. N., Merrill, J. E., 1952, Contr. Princ. Univ. Obs., 26, 32.
Smak, J., Stepien, K., 1968, this Colloquium. CoKon 65-46
Terashita, Y., Matsushima, S., 1966, Astrophys. J. Suppl., 13, 461.
Fig. 6. Same as in Fig. 2, for the phase phi = 180deg and the
inclination i = 75deg.
REFERENCES
Chandrasekhar, S., 1933, Mon. Not. R. astr. Soc. 93, 462 and 539.
Krzeminski, W., Kraft, R. P., 1964, Astrophys. J. 140, 921.
Kuiper, G. P., Johnson, J. R., 1956, Astrophys. J. 123, 90.
Plavec, M., Krotochvil, P., 1964, Bull. astr. Inst. Csl. 5, 165.
Rucinski, S. M., 1969a, Acta Astr. in preparation.
Rucinski, S. M., 1969b, Acta Astr. in preparation.
Russell, H. N., Merrill, J. E., 1952, Contr. Princ. Univ. Obs., 26, 32.
Smak, J., Stepien, K., 1968, this Colloquium. CoKon 65-46
Terashita, Y., Matsushima, S., 1966, Astrophys. J. Suppl., 13, 461.
 Fig. 1a. The shape of the WD secondary for Case 1 compared with its Roche lobe
(orbital plane section).
Fig. 1a. The shape of the WD secondary for Case 1 compared with its Roche lobe
(orbital plane section).
 Fig. 1b. Same as in Fig. 1a. for Case 2.
There is no theory which could be used to evaluate the expected values of
the coefficients C_1 and C_3, both the coefficients giving the asymmetry of the
light curve. The largest coefficient C_2, however, can be estimated on the
basis of the geometric parameters of the star and the limb (u) and gravity (y)
darkening coefficients determined from the same previously used model
atmospheres. The theoretical value of C_2 will be:
C'_2 = 15+u/10*(3-u)*(1+y)*epsilon,
where epsilon describes the shape of the star under the assumption of its
pure ellipticity. epsilon might be approximated by (Russell, Merrill 1952):
a) epsilon = (a - b)/a, where a and b are the two axes of the ellipsoid
lying in the orbital plane,
b) epsilon = 3/2 * (M_pri/M_WD) * (r/A)^3, where r is the mean radius of
the star, equal to the radius of a sphere of the same volume.
Comparing C'_2 computed in this way (for T_e = 7800deg, u = 0.627, and y =
= 0.785) with C_2 obtained previously, we have the following ratios C_2/C'_2:
a) b)
Case 1 1.70 1.60
Case 2 1.74 1.62
The simpler theory leads therefore to the value of C_2 which is 60-70 per cent
smaller than that obtained from the model described above.
As a check a modification of Case 1 was computed by assuming T_e = constant
over the whole surface of the star; that is, only the geometrical and limb
darkening effects were taken into account. The ratio C_2/C'_2 was then:
a) b)
C_2/C'_2 1.05 0.98
in general agreement with the rather approximate theory.
As we see the main effect increasing the observable amplitude of the
light variations is the strong dependence of the emerging intensity on
the gravitation via the effective temperature; this dependence cannot be
fully described by a simple gravity darkening coefficient. The dependence
also manifests itself in the distribution of the emerging intensity over
the star's disc and spots of different brightness are formed on it. The shape,
dimensions and intensity of these spots depend strongly on the orientation
relative to the observer (Fig. 2 and the following) and in the case of an
eclipsing system they might complicate very much the interpretation of the
light variations resulting from the eclipses.
More detailed description of the results presented here will be given
elsewhere (Rucinski 1969b).
The author is indebted to Dr. J. Smak for arousing his interest in the
subject.
Fig. 1b. Same as in Fig. 1a. for Case 2.
There is no theory which could be used to evaluate the expected values of
the coefficients C_1 and C_3, both the coefficients giving the asymmetry of the
light curve. The largest coefficient C_2, however, can be estimated on the
basis of the geometric parameters of the star and the limb (u) and gravity (y)
darkening coefficients determined from the same previously used model
atmospheres. The theoretical value of C_2 will be:
C'_2 = 15+u/10*(3-u)*(1+y)*epsilon,
where epsilon describes the shape of the star under the assumption of its
pure ellipticity. epsilon might be approximated by (Russell, Merrill 1952):
a) epsilon = (a - b)/a, where a and b are the two axes of the ellipsoid
lying in the orbital plane,
b) epsilon = 3/2 * (M_pri/M_WD) * (r/A)^3, where r is the mean radius of
the star, equal to the radius of a sphere of the same volume.
Comparing C'_2 computed in this way (for T_e = 7800deg, u = 0.627, and y =
= 0.785) with C_2 obtained previously, we have the following ratios C_2/C'_2:
a) b)
Case 1 1.70 1.60
Case 2 1.74 1.62
The simpler theory leads therefore to the value of C_2 which is 60-70 per cent
smaller than that obtained from the model described above.
As a check a modification of Case 1 was computed by assuming T_e = constant
over the whole surface of the star; that is, only the geometrical and limb
darkening effects were taken into account. The ratio C_2/C'_2 was then:
a) b)
C_2/C'_2 1.05 0.98
in general agreement with the rather approximate theory.
As we see the main effect increasing the observable amplitude of the
light variations is the strong dependence of the emerging intensity on
the gravitation via the effective temperature; this dependence cannot be
fully described by a simple gravity darkening coefficient. The dependence
also manifests itself in the distribution of the emerging intensity over
the star's disc and spots of different brightness are formed on it. The shape,
dimensions and intensity of these spots depend strongly on the orientation
relative to the observer (Fig. 2 and the following) and in the case of an
eclipsing system they might complicate very much the interpretation of the
light variations resulting from the eclipses.
More detailed description of the results presented here will be given
elsewhere (Rucinski 1969b).
The author is indebted to Dr. J. Smak for arousing his interest in the
subject.
 Fig. 2. The distribution of the emerging intensity over the visible disc
of the WD secondary. The mass ratio is 10 (Case 1). The isophotes are labelled
with numbers which should be multiplied by 10^-5 to give the intensity I_nu
in cgs units. The X-axis is directed towards the observer and the rotation
axis lies in the XZ-plane. The inclination of the orbit is i = 90deg;
the phase phi = 0deg, i.e, the star is viewed from the primary
component.
Fig. 2. The distribution of the emerging intensity over the visible disc
of the WD secondary. The mass ratio is 10 (Case 1). The isophotes are labelled
with numbers which should be multiplied by 10^-5 to give the intensity I_nu
in cgs units. The X-axis is directed towards the observer and the rotation
axis lies in the XZ-plane. The inclination of the orbit is i = 90deg;
the phase phi = 0deg, i.e, the star is viewed from the primary
component.
 Fig. 3. Same as in Fig. 2, for the phase phi = 90deg, i.e. the star is
viewed side-on.
Fig. 3. Same as in Fig. 2, for the phase phi = 90deg, i.e. the star is
viewed side-on.
 Fig. 4. Same as in Fig. 2, for the phase phi = 180deg, i.e. the opposite
side of the star is viewed.
Fig. 4. Same as in Fig. 2, for the phase phi = 180deg, i.e. the opposite
side of the star is viewed.
 Fig. 5. Same as in Fig. 2, for the phase phi = 0deg but for the inclination
i = 75deg.
Fig. 5. Same as in Fig. 2, for the phase phi = 0deg but for the inclination
i = 75deg.
 Fig. 6. Same as in Fig. 2, for the phase phi = 180deg and the
inclination i = 75deg.
REFERENCES
Chandrasekhar, S., 1933, Mon. Not. R. astr. Soc. 93, 462 and 539.
Krzeminski, W., Kraft, R. P., 1964, Astrophys. J. 140, 921.
Kuiper, G. P., Johnson, J. R., 1956, Astrophys. J. 123, 90.
Plavec, M., Krotochvil, P., 1964, Bull. astr. Inst. Csl. 5, 165.
Rucinski, S. M., 1969a, Acta Astr. in preparation.
Rucinski, S. M., 1969b, Acta Astr. in preparation.
Russell, H. N., Merrill, J. E., 1952, Contr. Princ. Univ. Obs., 26, 32.
Smak, J., Stepien, K., 1968, this Colloquium. CoKon 65-46
Terashita, Y., Matsushima, S., 1966, Astrophys. J. Suppl., 13, 461.
Fig. 6. Same as in Fig. 2, for the phase phi = 180deg and the
inclination i = 75deg.
REFERENCES
Chandrasekhar, S., 1933, Mon. Not. R. astr. Soc. 93, 462 and 539.
Krzeminski, W., Kraft, R. P., 1964, Astrophys. J. 140, 921.
Kuiper, G. P., Johnson, J. R., 1956, Astrophys. J. 123, 90.
Plavec, M., Krotochvil, P., 1964, Bull. astr. Inst. Csl. 5, 165.
Rucinski, S. M., 1969a, Acta Astr. in preparation.
Rucinski, S. M., 1969b, Acta Astr. in preparation.
Russell, H. N., Merrill, J. E., 1952, Contr. Princ. Univ. Obs., 26, 32.
Smak, J., Stepien, K., 1968, this Colloquium. CoKon 65-46
Terashita, Y., Matsushima, S., 1966, Astrophys. J. Suppl., 13, 461.