Non-Periodic Phenomena in Variable Stars
IAU Colloquium, Budapest, 1968
ANALYSE DES COURBES DE LUMIERE DES ETOILES DU TYPE
U GEMINORUM
MICHEL PETIT
Depuis 1963, j'ai cherche, en collaboration avec Mr Leon Menager, a
analyser les courbes de lumiere de plusieurs etoiles du type U Geminorum
suffisamment observees. De nombreux resultats ont ete publies, ou le
seront ulterieurement. Nous n'envisageons ici que les methodes
applicables a l'etude des liaisons et a l'analyse chronologique des
courbes de lumiere. Les resultats concernant la classification des
maxima et l'etude statistique des criteres de classification seront
publies par ailleurs.
ETUDE DES CORRELATIONS
Rappelons brievement le principe de la methode du calcul des
correlations pouvant exister entre deux donnees, par exemple entre deux
elements de la courbe de lumiere.
Soient n donnees de la variable xi et n' donnees de la variable yi ;
on nomme mx et my leurs moyennes. Le coefficient de correlation r se
definit comme suit:
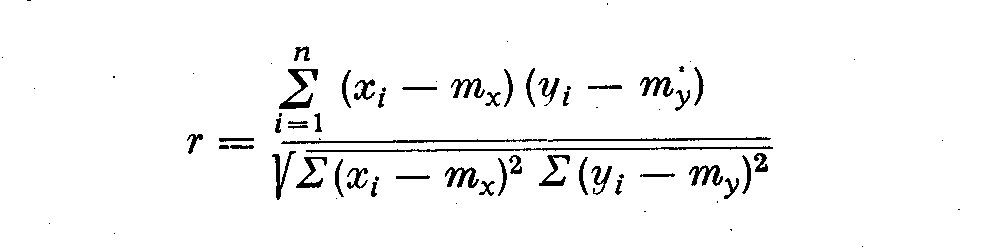 ou xi - mx et yi - my sont les ecarts par rapport aux moyennes mx et my .
Les ecarts-types se definissent par:
ou xi - mx et yi - my sont les ecarts par rapport aux moyennes mx et my .
Les ecarts-types se definissent par:
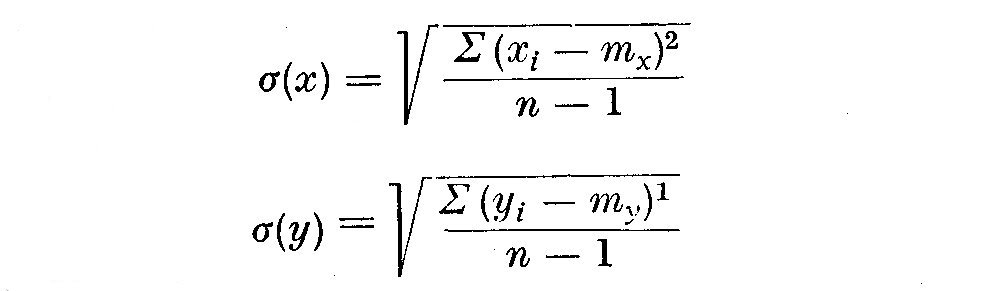 On peut demontrer que
-1 < = r < = +1
Pour juger de la valeur d'une correlation, on peut calculer l'ecart a la
valeur vraie:
On peut demontrer que
-1 < = r < = +1
Pour juger de la valeur d'une correlation, on peut calculer l'ecart a la
valeur vraie:
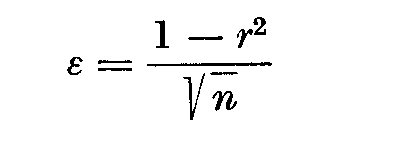 et considerer que la correlation est bonne, on pas, selon des valeurs
arbitraires de epsilon. Nous avons prefere uliliser la methode du
coefficient de Pearson. Il s'ecrit:
et considerer que la correlation est bonne, on pas, selon des valeurs
arbitraires de epsilon. Nous avons prefere uliliser la methode du
coefficient de Pearson. Il s'ecrit:
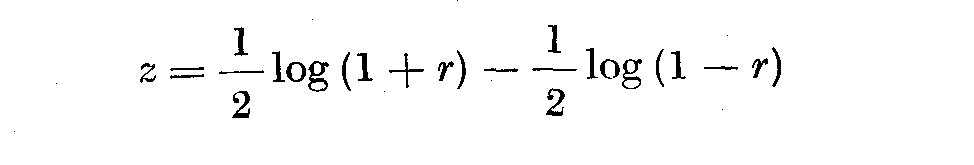 L'ecart reduit ti se calcule par la methode des chi2, t2i correspondant aux
differences Sigma(xi - xth)2.
Dans le cas d'une fausse liaison, on a t2 = 0, aux fluctuations aleatoires
pres, et la distribution est la meme que celle des chi2. Comme t n'est pas
lie a la moyenne des zi il est possible d'apprecier la signification d'un
groupe de correlation.
Menager et moi-meme avons calcule des coefficients de correlation entre
la magnitude, au maximum et au minimum, la largeur (1) des maxima et des
minima et deux autres donnees:
- l'energie totale E, calculee en prenant pour unite l'energie degagee
en un jour au minimum d'eclat (et exprimee en intensite lumineuse)
L'ecart reduit ti se calcule par la methode des chi2, t2i correspondant aux
differences Sigma(xi - xth)2.
Dans le cas d'une fausse liaison, on a t2 = 0, aux fluctuations aleatoires
pres, et la distribution est la meme que celle des chi2. Comme t n'est pas
lie a la moyenne des zi il est possible d'apprecier la signification d'un
groupe de correlation.
Menager et moi-meme avons calcule des coefficients de correlation entre
la magnitude, au maximum et au minimum, la largeur (1) des maxima et des
minima et deux autres donnees:
- l'energie totale E, calculee en prenant pour unite l'energie degagee
en un jour au minimum d'eclat (et exprimee en intensite lumineuse)
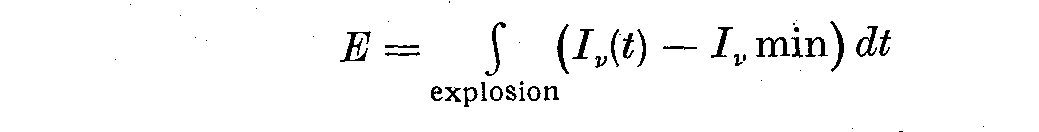 - la vitesse de croissance de l'eclat pendant la montee au maximum
- la vitesse de croissance de l'eclat pendant la montee au maximum
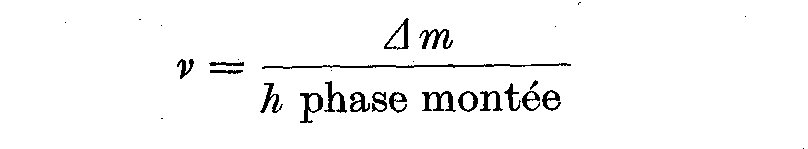 Le tableau suivant resume l'analyse faite pour quelques correlations
(n est le nombre d'etoiles etudiees)
Correlations n chi2 p(chi2 > chi02) Valeur
1 max-V 9 8,23 0,50 faible
1 max-E 9 84,79 <0,01 bonne
E-V 9 22,86 0,06 moyenne
1 max-mv max 15 74,04 <=0,001 bonne
1 min-mv min 5 24,52 0,04 moyenne
La liaison entre 1 min t mv min, signalee par Campbell (1933) sur
SS Cygni, confirmee par Martel (1961) a ete retrouvee par l'auteur sur cinq
autres etoiles observees au minimum. Sa valeur moyenne, relativement
faible, est probablement due a l'incertitude des observations utilisees.
ANALYSE DES SUITES DE MAXIMA
Soient mx et my les valeurs moyennes des intervalles et des largeurs
des maxima, nx et nx le nombre des echantillons, sigmax t sigmay les
dispersions correspondantes. Si ces valeurs sont distribuees au hasard,
nous aurons, puisque les moyennes sorit independantes:
mx - my = 0
L'ecart reduit t vaut:
Le tableau suivant resume l'analyse faite pour quelques correlations
(n est le nombre d'etoiles etudiees)
Correlations n chi2 p(chi2 > chi02) Valeur
1 max-V 9 8,23 0,50 faible
1 max-E 9 84,79 <0,01 bonne
E-V 9 22,86 0,06 moyenne
1 max-mv max 15 74,04 <=0,001 bonne
1 min-mv min 5 24,52 0,04 moyenne
La liaison entre 1 min t mv min, signalee par Campbell (1933) sur
SS Cygni, confirmee par Martel (1961) a ete retrouvee par l'auteur sur cinq
autres etoiles observees au minimum. Sa valeur moyenne, relativement
faible, est probablement due a l'incertitude des observations utilisees.
ANALYSE DES SUITES DE MAXIMA
Soient mx et my les valeurs moyennes des intervalles et des largeurs
des maxima, nx et nx le nombre des echantillons, sigmax t sigmay les
dispersions correspondantes. Si ces valeurs sont distribuees au hasard,
nous aurons, puisque les moyennes sorit independantes:
mx - my = 0
L'ecart reduit t vaut:
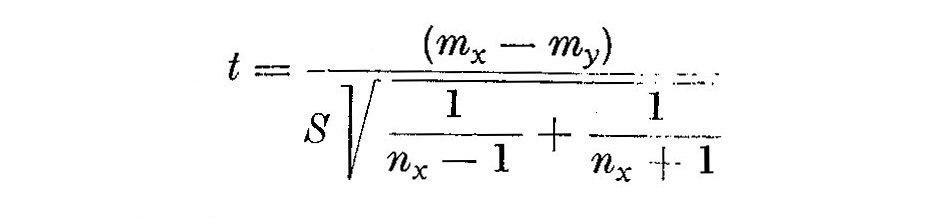 ou S, degre de liberte totale, s'exprime par
ou S, degre de liberte totale, s'exprime par
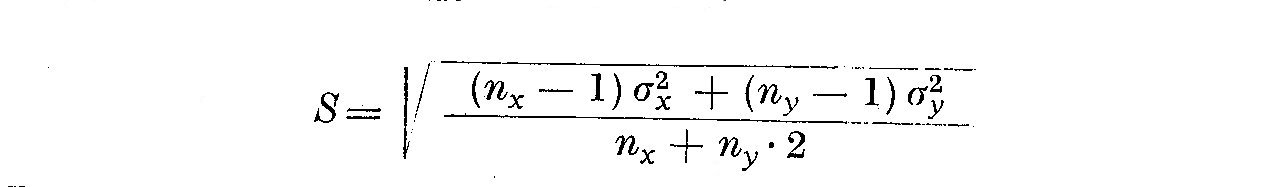 Les ecarts-types sont
Les ecarts-types sont
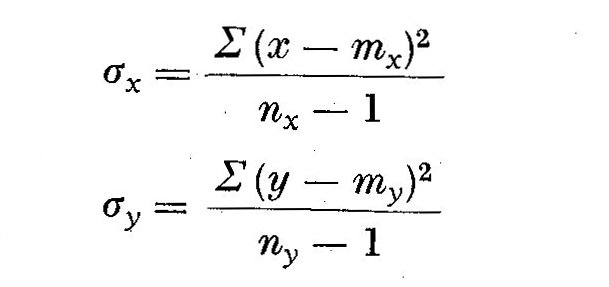 On demontre ainsi que les families dc maxima se groupent en deux
classes, selon les valeurs de t, l'une comprenant les maxima d'ordre
court (C ou SC), l'autre les maxima d'ordre long (L ou SL).*
-----------------------------------------------------------------
* La classification adoptee par l'auteur, tres proche de celle etablie
par Mme Lortet-Zuckermann (1961), (1964) est la suivante:
maxima normaux longs L
maxima normaux courts C
maxima symetriques longs SL
maxima symetriques courts SC
maxima faibles F
-----------------------------------------------------------------
Appelons evenement A les maxima d'ordre court, et B les maxima d'ordre
long des observations fournissent de A t B disposees comme la suivante:
3A 5A 2A 1A 3A etc...
1B 1B 2B 1B 1B
Soit une serie chronologique comprenant m fois A et n fois B. Cet ensemble
peut etre considere comme une suite de tirages independants d'elements
distincts. Un schema d'urne montre que le nombre de variations d'une
teile suite est une variable aleatoire de moyenne Rth, dans le cas
d'une variable gaussienne, telle que:
On demontre ainsi que les families dc maxima se groupent en deux
classes, selon les valeurs de t, l'une comprenant les maxima d'ordre
court (C ou SC), l'autre les maxima d'ordre long (L ou SL).*
-----------------------------------------------------------------
* La classification adoptee par l'auteur, tres proche de celle etablie
par Mme Lortet-Zuckermann (1961), (1964) est la suivante:
maxima normaux longs L
maxima normaux courts C
maxima symetriques longs SL
maxima symetriques courts SC
maxima faibles F
-----------------------------------------------------------------
Appelons evenement A les maxima d'ordre court, et B les maxima d'ordre
long des observations fournissent de A t B disposees comme la suivante:
3A 5A 2A 1A 3A etc...
1B 1B 2B 1B 1B
Soit une serie chronologique comprenant m fois A et n fois B. Cet ensemble
peut etre considere comme une suite de tirages independants d'elements
distincts. Un schema d'urne montre que le nombre de variations d'une
teile suite est une variable aleatoire de moyenne Rth, dans le cas
d'une variable gaussienne, telle que:
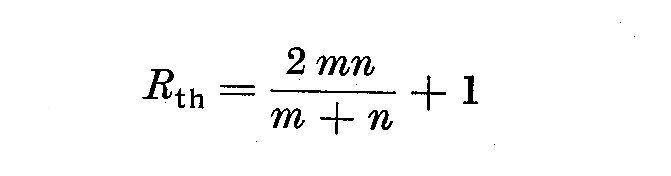 de variance
de variance
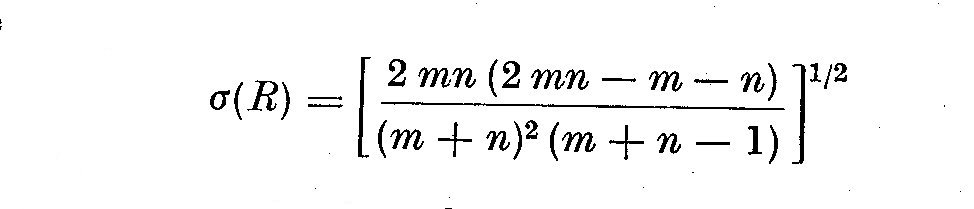 L'ecart reduit t, qui suit la loi de Gauss, s'ecrit:
L'ecart reduit t, qui suit la loi de Gauss, s'ecrit:
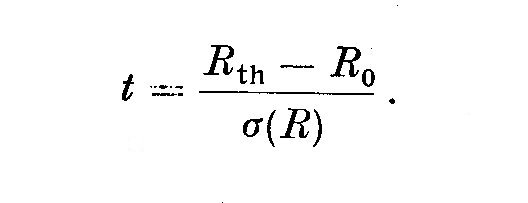 Si la serie est aleatoire, la probabilite de trouver t > t, s'ecrit:
Si la serie est aleatoire, la probabilite de trouver t > t, s'ecrit:
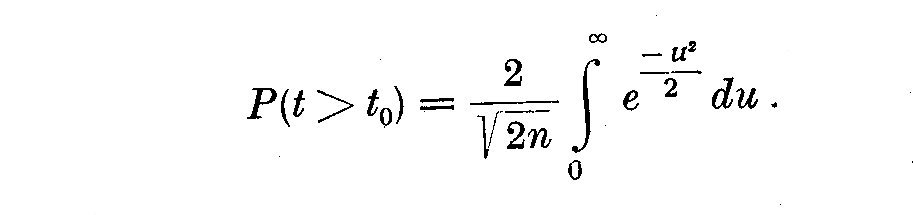 Une telle analyse a ete faite pour six etoiles (tableau suivant);
Lorsque est positif, les evenements A et B ont tendance a se grouper,
quand t este negativ, ils ont tendance a alterner
Etoiles R_0 sigma(R) t P(t>t0) Auteur
SS Aur 32,1 3,3 -3,7 0,0001 Menager
Z Cam 23 2,4 4,1 0,00002 Menager
U Gem 53,2 5,5 3,3 0,0001 Petit
VW Hyi 42,9 4,1 2,6 0,009 Menager
CN Ori 97 8,5 3,2 0,0001 Petit
TZ Per 45 4,1 3,6 0,0001 Petit
La meme methode permet de mettre en evidence la tendance au groupement
des maxima symetriques, des maxima faibles des oscillations (Lortet,
1964) et d'autres epoques erratiques.
Cette methode a ete aussi utilisee pour l'etude des variations non
normales de deux etoiles du groupe Z Camelopardalis; noun appelons
evenement A les suites variations normales-variations erratiques,
evenement B les suites variations normales-paliers. On obtient:
R_0 sigma(R) t P(t0 > t0)
Z Cam 13,4 1,9 3,9 0,0001
TZ Per 23,5 3,4 3,3 0,001
Menager et Petit (5) ont montre, pour VW Hyi, que pour les series de
maxima d'ordre court, les largeurs des minima sont d'autant plus petites que
le nombre de maxima courts successifs est plus eleve. J'ai verifie ser une
douzaine d'etoiles que ce phenomene existe dans tous les cas. Il semble
done que, lorsque des maxima d'ordre courts se surcedent, leur processus
de formation a tendance a s'accelerer. L'etude approfondie de ce
phenomene reste a faire, mais on note que les distributions de mv max, l
max et E sont sensiblement les memes pour les maxima d'ordre C alternes
avec des maxima d'ordre L et pour des maxima C formant une serie.
ANALYSE CHRONOLOGIQUE DES VARIATIONS LUMINEUSES
Nous avons utilise quatre methodes d'etude, que voici:
1. Les chaines de Markov
Considerons une suite chronologique d'etats E, observes a des instants
t, tels que l'on ait E(i1, t1), E(i2, t2) ... E(in, tn) ou i = 1, 2, ... n.
Par definition, une telle suite obeit a une chaine de Markov simple si, quels que soient
n et j, la probabilite d'observer un etat donne E(j) a l'instant tn + 1 ne depend
que de l'etat precedent E (in, tn) et non pas des etats anterieurs.
L'observation permet d'etablir une matrice carree d'ordre r, dite matrice
de transition |PK|
La probabilite P[E(j,tn+1)/E(in, tn)] est appelee probabilite de
transition en une epreuve. Elle est representee par une matrice [P1](ou k = 1).
On peut aussi calculer des matrices de transition en p epreuves, pour
lesquelles:
P[E(j, tn+1)/E(i, tn-p+1)] = [P1]pj
Dans la pratique on calcule des matrices de transition en deux et trois
epreuves, [P2] et [P3] et on les compare avee le carre et le cube de la
matrice [P1] observee.
Si l'on a:
[P1]2~=[P2]
[P1]2~=[P3]
(relation de Chapman-Kolmogorov) c'est que les maxima evoluent suivant
une chaine de Markov simple: la nature d'un maximum depend alors du maximum
precedent et seulement de celui-ci.
Martel (1961) avait signale que c'est le cas de SS Cygni, mais Mme Lortet
(1964, 1966) appliquant divers tests sur le caractere aleatoire d'une serie de
deux ou trois parametres, arrive aux conclusions suivantes:
- la succession des maxima de caractere long et non-long est assez
bien representee par une chaine de Markov d'ordre 1, mais notons que SS Cygni
a une nette tendance a l'alternance reguliere des deux types, ce qui
n'est pas le cas de toutes les etoiles que nous avons etudie.
- la succession des maxima faibles (F) et non faibles peut se representer
par une chaine de Markov d'ordre 2.
- un schema markovien d'ordre 1, 2 ou plus n'explique pas l'existance
des series de maxima courts, ou des periodes erratiques, riches en variations
irregulieres.
Mme Lortet a donc propose un schema d'evenement recurrent ou les structures
successives sont independantes, ont chacune une certaine probabilite, et
ou l'evenement est constitute par un changement de structure. Ces structures
cycliques peuvent etre, soit les suites long-court, les suites
court-court et les variations non normales (oscillations, paliers, etc ...).
Pour plusieurs etoiles, Menager et moi avons applique deux tests, l'un
en calculant des matrices theoriques normalisees, et en appliquant a ces
matrices normalisees |Pk| un test en chi2 des transitions en une epreuve, l'autre
en calculant des matrices [P1]2 et [P1]3, deduites de [P1], malgre la
difficulte de leur attribuer un intervalle de confiance, et en les
comparant aux matrices [P2] et [P3].
Les resultats obtenus sont resumes par le tableau suivant:
Variables m chi[P2] P(chi2>chi02) chi[P3] P(chi2>chi02) Auteur
SS Aur 4 11,54 0,02 5,19 0,25 (7)
Z Cam 1 5,30 0,025 Menager
U Gem 1 10,8 0,01 4,7 0,16 Petit
VW Hyi 1 3,44 0,07 3,2 0,08 Menager
CN Ori 1 4,7 0,04 Petit
Dans tous les cas il n'apparait pas que l'on soit devant une chain de
Markov simple.
2. La fonction d'autocorrelation
Il faut remarquer que la suite des intervalles peut etre markovienne
sans que la suite des maxima le soit. Menager a repris l'analyse, en
calculant une fonction d'autocorrelation, ou le coefficient
d'autocorrelation r(p) est defini par:
Une telle analyse a ete faite pour six etoiles (tableau suivant);
Lorsque est positif, les evenements A et B ont tendance a se grouper,
quand t este negativ, ils ont tendance a alterner
Etoiles R_0 sigma(R) t P(t>t0) Auteur
SS Aur 32,1 3,3 -3,7 0,0001 Menager
Z Cam 23 2,4 4,1 0,00002 Menager
U Gem 53,2 5,5 3,3 0,0001 Petit
VW Hyi 42,9 4,1 2,6 0,009 Menager
CN Ori 97 8,5 3,2 0,0001 Petit
TZ Per 45 4,1 3,6 0,0001 Petit
La meme methode permet de mettre en evidence la tendance au groupement
des maxima symetriques, des maxima faibles des oscillations (Lortet,
1964) et d'autres epoques erratiques.
Cette methode a ete aussi utilisee pour l'etude des variations non
normales de deux etoiles du groupe Z Camelopardalis; noun appelons
evenement A les suites variations normales-variations erratiques,
evenement B les suites variations normales-paliers. On obtient:
R_0 sigma(R) t P(t0 > t0)
Z Cam 13,4 1,9 3,9 0,0001
TZ Per 23,5 3,4 3,3 0,001
Menager et Petit (5) ont montre, pour VW Hyi, que pour les series de
maxima d'ordre court, les largeurs des minima sont d'autant plus petites que
le nombre de maxima courts successifs est plus eleve. J'ai verifie ser une
douzaine d'etoiles que ce phenomene existe dans tous les cas. Il semble
done que, lorsque des maxima d'ordre courts se surcedent, leur processus
de formation a tendance a s'accelerer. L'etude approfondie de ce
phenomene reste a faire, mais on note que les distributions de mv max, l
max et E sont sensiblement les memes pour les maxima d'ordre C alternes
avec des maxima d'ordre L et pour des maxima C formant une serie.
ANALYSE CHRONOLOGIQUE DES VARIATIONS LUMINEUSES
Nous avons utilise quatre methodes d'etude, que voici:
1. Les chaines de Markov
Considerons une suite chronologique d'etats E, observes a des instants
t, tels que l'on ait E(i1, t1), E(i2, t2) ... E(in, tn) ou i = 1, 2, ... n.
Par definition, une telle suite obeit a une chaine de Markov simple si, quels que soient
n et j, la probabilite d'observer un etat donne E(j) a l'instant tn + 1 ne depend
que de l'etat precedent E (in, tn) et non pas des etats anterieurs.
L'observation permet d'etablir une matrice carree d'ordre r, dite matrice
de transition |PK|
La probabilite P[E(j,tn+1)/E(in, tn)] est appelee probabilite de
transition en une epreuve. Elle est representee par une matrice [P1](ou k = 1).
On peut aussi calculer des matrices de transition en p epreuves, pour
lesquelles:
P[E(j, tn+1)/E(i, tn-p+1)] = [P1]pj
Dans la pratique on calcule des matrices de transition en deux et trois
epreuves, [P2] et [P3] et on les compare avee le carre et le cube de la
matrice [P1] observee.
Si l'on a:
[P1]2~=[P2]
[P1]2~=[P3]
(relation de Chapman-Kolmogorov) c'est que les maxima evoluent suivant
une chaine de Markov simple: la nature d'un maximum depend alors du maximum
precedent et seulement de celui-ci.
Martel (1961) avait signale que c'est le cas de SS Cygni, mais Mme Lortet
(1964, 1966) appliquant divers tests sur le caractere aleatoire d'une serie de
deux ou trois parametres, arrive aux conclusions suivantes:
- la succession des maxima de caractere long et non-long est assez
bien representee par une chaine de Markov d'ordre 1, mais notons que SS Cygni
a une nette tendance a l'alternance reguliere des deux types, ce qui
n'est pas le cas de toutes les etoiles que nous avons etudie.
- la succession des maxima faibles (F) et non faibles peut se representer
par une chaine de Markov d'ordre 2.
- un schema markovien d'ordre 1, 2 ou plus n'explique pas l'existance
des series de maxima courts, ou des periodes erratiques, riches en variations
irregulieres.
Mme Lortet a donc propose un schema d'evenement recurrent ou les structures
successives sont independantes, ont chacune une certaine probabilite, et
ou l'evenement est constitute par un changement de structure. Ces structures
cycliques peuvent etre, soit les suites long-court, les suites
court-court et les variations non normales (oscillations, paliers, etc ...).
Pour plusieurs etoiles, Menager et moi avons applique deux tests, l'un
en calculant des matrices theoriques normalisees, et en appliquant a ces
matrices normalisees |Pk| un test en chi2 des transitions en une epreuve, l'autre
en calculant des matrices [P1]2 et [P1]3, deduites de [P1], malgre la
difficulte de leur attribuer un intervalle de confiance, et en les
comparant aux matrices [P2] et [P3].
Les resultats obtenus sont resumes par le tableau suivant:
Variables m chi[P2] P(chi2>chi02) chi[P3] P(chi2>chi02) Auteur
SS Aur 4 11,54 0,02 5,19 0,25 (7)
Z Cam 1 5,30 0,025 Menager
U Gem 1 10,8 0,01 4,7 0,16 Petit
VW Hyi 1 3,44 0,07 3,2 0,08 Menager
CN Ori 1 4,7 0,04 Petit
Dans tous les cas il n'apparait pas que l'on soit devant une chain de
Markov simple.
2. La fonction d'autocorrelation
Il faut remarquer que la suite des intervalles peut etre markovienne
sans que la suite des maxima le soit. Menager a repris l'analyse, en
calculant une fonction d'autocorrelation, ou le coefficient
d'autocorrelation r(p) est defini par:
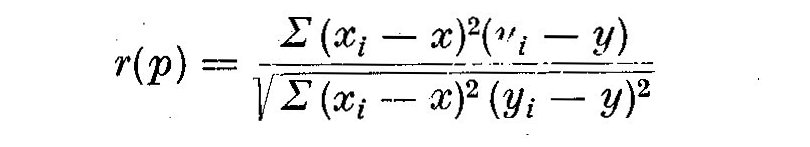 ou p est l'ordre du maximum suivant, et ou
ou p est l'ordre du maximum suivant, et ou
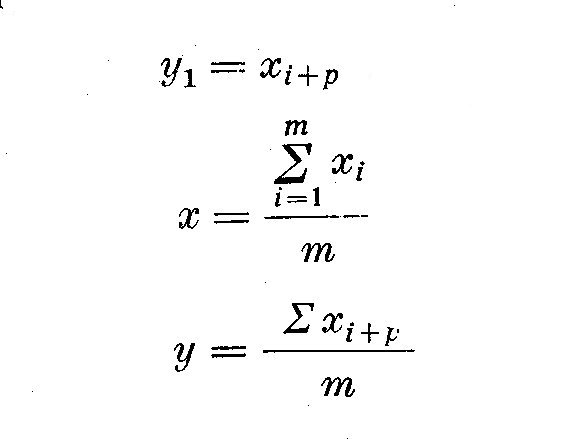 On a
On a
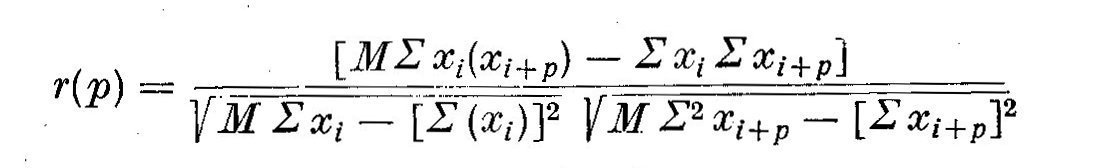 m etant le nombre de termes et N le nombre de couples observes (M = N + p).
On calcule ensuite lea variances en chaque point par
m etant le nombre de termes et N le nombre de couples observes (M = N + p).
On calcule ensuite lea variances en chaque point par
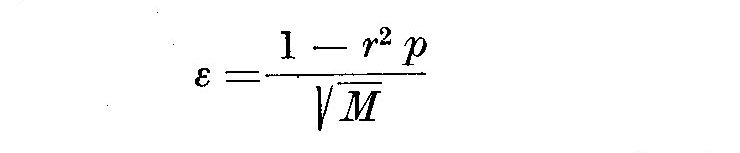 Pour SS Aur et pour Z Cam l'autocorrelogramme des intervalles suggere
une chaine de Markov d'ordre 4 ou plus; pour V W Hyi, la suite des intervalles
semble suivre un processus markovien simple, tandis que la suite des maxima
obeit a un processes d'ordre >=4.
3. Calcul du temps de retour
Le temps de retour est le nombre d'epreuves necessaires pour le retour a
un etat specifie, c'est a dire le nombre theorique de suites long-non long
que l'on compare ensuite aux nombres observes.
Pour Z Cam on observe, par rapport au calcul d'une matrice theorique,
un deficit de transition pour les suites de maxima courts d'ordre 1, ou d'ordre
>4, et un exces de transition pour les valeurs moyennes.
On conclut que lea suites de maxima longs suivent un schema conforme
a celui de la matrice [P1] en une epreuve, tandis que les suites de maxima
courts se rapprochent du schema d'un tirage exhaustif d'evenements A et B
absolument aleatoires.
4. Test de recurrence
Cette methode a ete utilisee pour l'analyse des l min. On pose
Pour SS Aur et pour Z Cam l'autocorrelogramme des intervalles suggere
une chaine de Markov d'ordre 4 ou plus; pour V W Hyi, la suite des intervalles
semble suivre un processus markovien simple, tandis que la suite des maxima
obeit a un processes d'ordre >=4.
3. Calcul du temps de retour
Le temps de retour est le nombre d'epreuves necessaires pour le retour a
un etat specifie, c'est a dire le nombre theorique de suites long-non long
que l'on compare ensuite aux nombres observes.
Pour Z Cam on observe, par rapport au calcul d'une matrice theorique,
un deficit de transition pour les suites de maxima courts d'ordre 1, ou d'ordre
>4, et un exces de transition pour les valeurs moyennes.
On conclut que lea suites de maxima longs suivent un schema conforme
a celui de la matrice [P1] en une epreuve, tandis que les suites de maxima
courts se rapprochent du schema d'un tirage exhaustif d'evenements A et B
absolument aleatoires.
4. Test de recurrence
Cette methode a ete utilisee pour l'analyse des l min. On pose
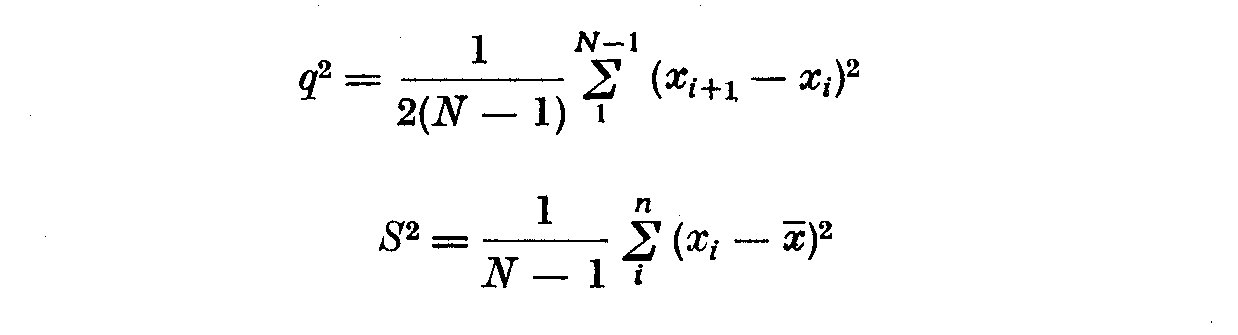 q2 etant la variance de 2 valeurs successives de la variable x et S2 la
variance de x. Soit
q2 etant la variance de 2 valeurs successives de la variable x et S2 la
variance de x. Soit
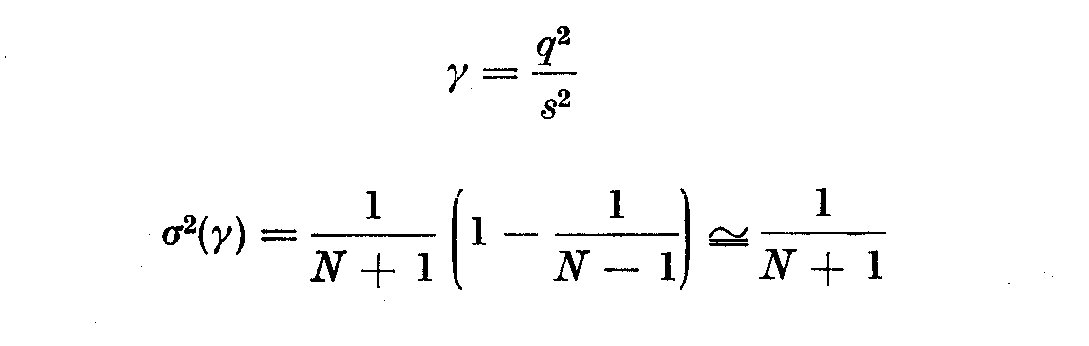 Pour Z Cam on obtient q2 = 25, S2 = 36,2 gamma = 0,69. Le test de Student
nous donne:
t = 1-gamma/sigma gamma = 5.1 p(t>t0)<10^-6
ce qui indique une tendance a la recurrence. Les calculs effectues sur SS Aur
et U Gem confirment ce phenomene; dans ces deux cas p(t>t0)<10^-5.
Ainsi notre analyse confirme qu'un schema de chaine markovienne, s'il
suffit dans certains cas, a l'etude de la succession des intervalles n'explique
ni la tendance au groupement des maxima faibles ou symetriques, ni l'existence
de periodes erratiques diverses. Il semble donc preferable d'adopter un
schema d'evenement recurrent, mais une analyse complete demandera de disposer
de series de maxima longues et continues et d'une bonne classification
des phenomenes observes.
REFERENCES
Campbell, L., 1933, Ann. Harv. Coll. Obs., 90, No. 3.
Lortet-Zuckermann, M. C., 1964, Ann. Astrophys. 27, 65.
Lortet-Zuckermann, M. C., 1966, Ann. Astrophys. 29, 205.
Martel, L., 1961, Ann. Astrophys. 24, 267.
Menager, L. et Petit, M., (a paraitre).
Petit, M. et Menager, L., 1963, Ciel Terre 79, 407.
Zuckermann, M. C., 1961, Ann. Astrophys. 24, 431.
Pour Z Cam on obtient q2 = 25, S2 = 36,2 gamma = 0,69. Le test de Student
nous donne:
t = 1-gamma/sigma gamma = 5.1 p(t>t0)<10^-6
ce qui indique une tendance a la recurrence. Les calculs effectues sur SS Aur
et U Gem confirment ce phenomene; dans ces deux cas p(t>t0)<10^-5.
Ainsi notre analyse confirme qu'un schema de chaine markovienne, s'il
suffit dans certains cas, a l'etude de la succession des intervalles n'explique
ni la tendance au groupement des maxima faibles ou symetriques, ni l'existence
de periodes erratiques diverses. Il semble donc preferable d'adopter un
schema d'evenement recurrent, mais une analyse complete demandera de disposer
de series de maxima longues et continues et d'une bonne classification
des phenomenes observes.
REFERENCES
Campbell, L., 1933, Ann. Harv. Coll. Obs., 90, No. 3.
Lortet-Zuckermann, M. C., 1964, Ann. Astrophys. 27, 65.
Lortet-Zuckermann, M. C., 1966, Ann. Astrophys. 29, 205.
Martel, L., 1961, Ann. Astrophys. 24, 267.
Menager, L. et Petit, M., (a paraitre).
Petit, M. et Menager, L., 1963, Ciel Terre 79, 407.
Zuckermann, M. C., 1961, Ann. Astrophys. 24, 431.
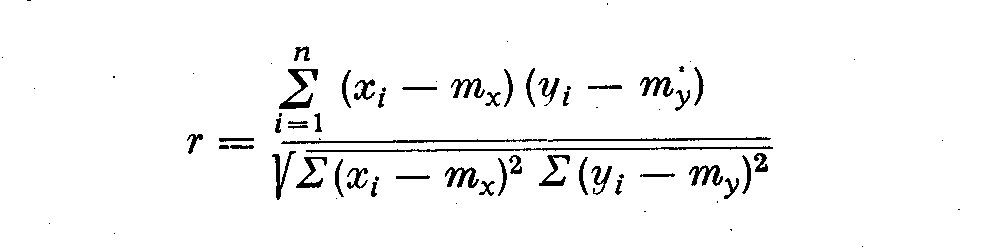 ou xi - mx et yi - my sont les ecarts par rapport aux moyennes mx et my .
Les ecarts-types se definissent par:
ou xi - mx et yi - my sont les ecarts par rapport aux moyennes mx et my .
Les ecarts-types se definissent par:
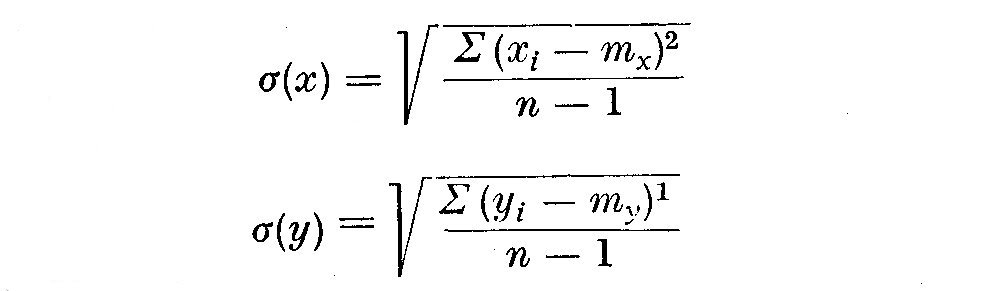 On peut demontrer que
-1 < = r < = +1
Pour juger de la valeur d'une correlation, on peut calculer l'ecart a la
valeur vraie:
On peut demontrer que
-1 < = r < = +1
Pour juger de la valeur d'une correlation, on peut calculer l'ecart a la
valeur vraie:
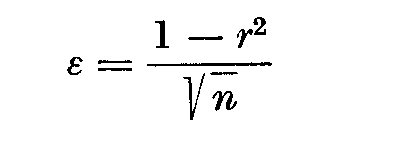 et considerer que la correlation est bonne, on pas, selon des valeurs
arbitraires de epsilon. Nous avons prefere uliliser la methode du
coefficient de Pearson. Il s'ecrit:
et considerer que la correlation est bonne, on pas, selon des valeurs
arbitraires de epsilon. Nous avons prefere uliliser la methode du
coefficient de Pearson. Il s'ecrit:
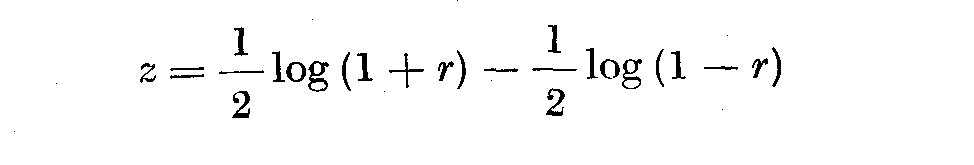 L'ecart reduit ti se calcule par la methode des chi2, t2i correspondant aux
differences Sigma(xi - xth)2.
Dans le cas d'une fausse liaison, on a t2 = 0, aux fluctuations aleatoires
pres, et la distribution est la meme que celle des chi2. Comme t n'est pas
lie a la moyenne des zi il est possible d'apprecier la signification d'un
groupe de correlation.
Menager et moi-meme avons calcule des coefficients de correlation entre
la magnitude, au maximum et au minimum, la largeur (1) des maxima et des
minima et deux autres donnees:
- l'energie totale E, calculee en prenant pour unite l'energie degagee
en un jour au minimum d'eclat (et exprimee en intensite lumineuse)
L'ecart reduit ti se calcule par la methode des chi2, t2i correspondant aux
differences Sigma(xi - xth)2.
Dans le cas d'une fausse liaison, on a t2 = 0, aux fluctuations aleatoires
pres, et la distribution est la meme que celle des chi2. Comme t n'est pas
lie a la moyenne des zi il est possible d'apprecier la signification d'un
groupe de correlation.
Menager et moi-meme avons calcule des coefficients de correlation entre
la magnitude, au maximum et au minimum, la largeur (1) des maxima et des
minima et deux autres donnees:
- l'energie totale E, calculee en prenant pour unite l'energie degagee
en un jour au minimum d'eclat (et exprimee en intensite lumineuse)
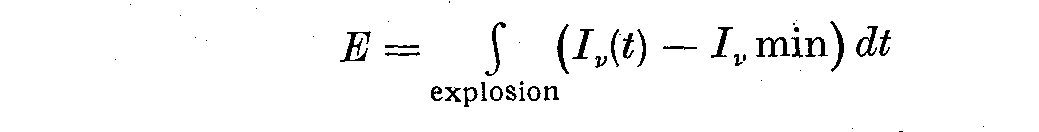 - la vitesse de croissance de l'eclat pendant la montee au maximum
- la vitesse de croissance de l'eclat pendant la montee au maximum
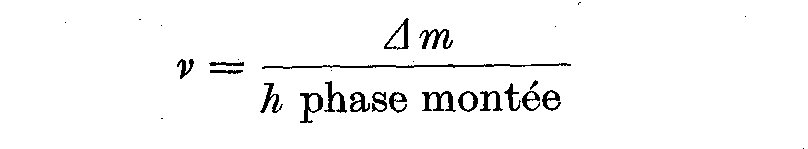 Le tableau suivant resume l'analyse faite pour quelques correlations
(n est le nombre d'etoiles etudiees)
Correlations n chi2 p(chi2 > chi02) Valeur
1 max-V 9 8,23 0,50 faible
1 max-E 9 84,79 <0,01 bonne
E-V 9 22,86 0,06 moyenne
1 max-mv max 15 74,04 <=0,001 bonne
1 min-mv min 5 24,52 0,04 moyenne
La liaison entre 1 min t mv min, signalee par Campbell (1933) sur
SS Cygni, confirmee par Martel (1961) a ete retrouvee par l'auteur sur cinq
autres etoiles observees au minimum. Sa valeur moyenne, relativement
faible, est probablement due a l'incertitude des observations utilisees.
ANALYSE DES SUITES DE MAXIMA
Soient mx et my les valeurs moyennes des intervalles et des largeurs
des maxima, nx et nx le nombre des echantillons, sigmax t sigmay les
dispersions correspondantes. Si ces valeurs sont distribuees au hasard,
nous aurons, puisque les moyennes sorit independantes:
mx - my = 0
L'ecart reduit t vaut:
Le tableau suivant resume l'analyse faite pour quelques correlations
(n est le nombre d'etoiles etudiees)
Correlations n chi2 p(chi2 > chi02) Valeur
1 max-V 9 8,23 0,50 faible
1 max-E 9 84,79 <0,01 bonne
E-V 9 22,86 0,06 moyenne
1 max-mv max 15 74,04 <=0,001 bonne
1 min-mv min 5 24,52 0,04 moyenne
La liaison entre 1 min t mv min, signalee par Campbell (1933) sur
SS Cygni, confirmee par Martel (1961) a ete retrouvee par l'auteur sur cinq
autres etoiles observees au minimum. Sa valeur moyenne, relativement
faible, est probablement due a l'incertitude des observations utilisees.
ANALYSE DES SUITES DE MAXIMA
Soient mx et my les valeurs moyennes des intervalles et des largeurs
des maxima, nx et nx le nombre des echantillons, sigmax t sigmay les
dispersions correspondantes. Si ces valeurs sont distribuees au hasard,
nous aurons, puisque les moyennes sorit independantes:
mx - my = 0
L'ecart reduit t vaut:
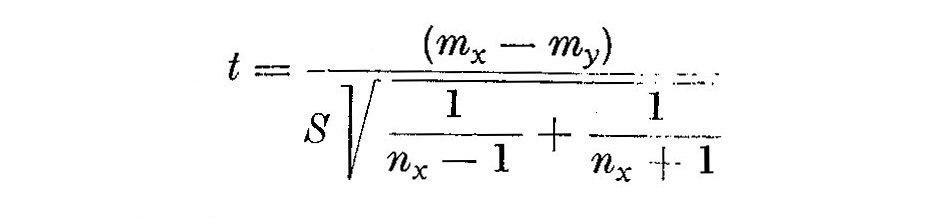 ou S, degre de liberte totale, s'exprime par
ou S, degre de liberte totale, s'exprime par
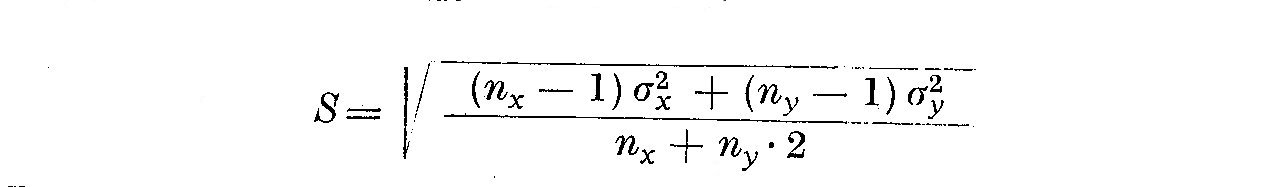 Les ecarts-types sont
Les ecarts-types sont
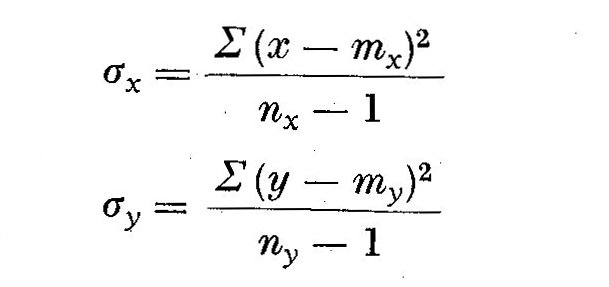 On demontre ainsi que les families dc maxima se groupent en deux
classes, selon les valeurs de t, l'une comprenant les maxima d'ordre
court (C ou SC), l'autre les maxima d'ordre long (L ou SL).*
-----------------------------------------------------------------
* La classification adoptee par l'auteur, tres proche de celle etablie
par Mme Lortet-Zuckermann (1961), (1964) est la suivante:
maxima normaux longs L
maxima normaux courts C
maxima symetriques longs SL
maxima symetriques courts SC
maxima faibles F
-----------------------------------------------------------------
Appelons evenement A les maxima d'ordre court, et B les maxima d'ordre
long des observations fournissent de A t B disposees comme la suivante:
3A 5A 2A 1A 3A etc...
1B 1B 2B 1B 1B
Soit une serie chronologique comprenant m fois A et n fois B. Cet ensemble
peut etre considere comme une suite de tirages independants d'elements
distincts. Un schema d'urne montre que le nombre de variations d'une
teile suite est une variable aleatoire de moyenne Rth, dans le cas
d'une variable gaussienne, telle que:
On demontre ainsi que les families dc maxima se groupent en deux
classes, selon les valeurs de t, l'une comprenant les maxima d'ordre
court (C ou SC), l'autre les maxima d'ordre long (L ou SL).*
-----------------------------------------------------------------
* La classification adoptee par l'auteur, tres proche de celle etablie
par Mme Lortet-Zuckermann (1961), (1964) est la suivante:
maxima normaux longs L
maxima normaux courts C
maxima symetriques longs SL
maxima symetriques courts SC
maxima faibles F
-----------------------------------------------------------------
Appelons evenement A les maxima d'ordre court, et B les maxima d'ordre
long des observations fournissent de A t B disposees comme la suivante:
3A 5A 2A 1A 3A etc...
1B 1B 2B 1B 1B
Soit une serie chronologique comprenant m fois A et n fois B. Cet ensemble
peut etre considere comme une suite de tirages independants d'elements
distincts. Un schema d'urne montre que le nombre de variations d'une
teile suite est une variable aleatoire de moyenne Rth, dans le cas
d'une variable gaussienne, telle que:
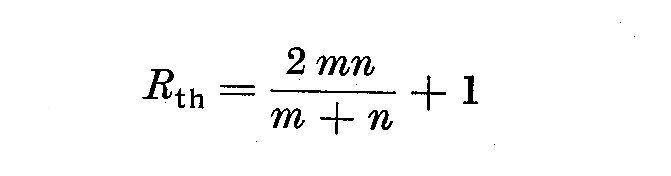 de variance
de variance
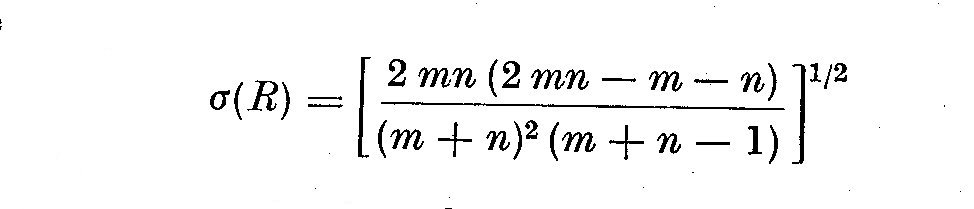 L'ecart reduit t, qui suit la loi de Gauss, s'ecrit:
L'ecart reduit t, qui suit la loi de Gauss, s'ecrit:
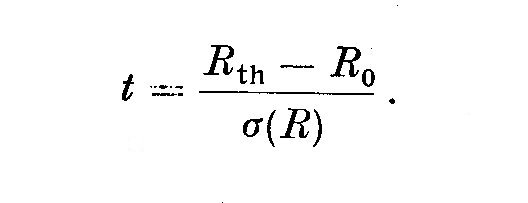 Si la serie est aleatoire, la probabilite de trouver t > t, s'ecrit:
Si la serie est aleatoire, la probabilite de trouver t > t, s'ecrit:
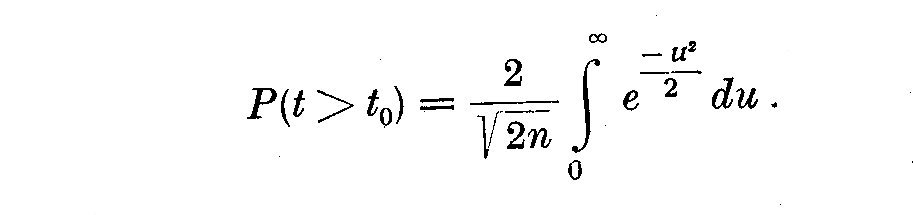 Une telle analyse a ete faite pour six etoiles (tableau suivant);
Lorsque est positif, les evenements A et B ont tendance a se grouper,
quand t este negativ, ils ont tendance a alterner
Etoiles R_0 sigma(R) t P(t>t0) Auteur
SS Aur 32,1 3,3 -3,7 0,0001 Menager
Z Cam 23 2,4 4,1 0,00002 Menager
U Gem 53,2 5,5 3,3 0,0001 Petit
VW Hyi 42,9 4,1 2,6 0,009 Menager
CN Ori 97 8,5 3,2 0,0001 Petit
TZ Per 45 4,1 3,6 0,0001 Petit
La meme methode permet de mettre en evidence la tendance au groupement
des maxima symetriques, des maxima faibles des oscillations (Lortet,
1964) et d'autres epoques erratiques.
Cette methode a ete aussi utilisee pour l'etude des variations non
normales de deux etoiles du groupe Z Camelopardalis; noun appelons
evenement A les suites variations normales-variations erratiques,
evenement B les suites variations normales-paliers. On obtient:
R_0 sigma(R) t P(t0 > t0)
Z Cam 13,4 1,9 3,9 0,0001
TZ Per 23,5 3,4 3,3 0,001
Menager et Petit (5) ont montre, pour VW Hyi, que pour les series de
maxima d'ordre court, les largeurs des minima sont d'autant plus petites que
le nombre de maxima courts successifs est plus eleve. J'ai verifie ser une
douzaine d'etoiles que ce phenomene existe dans tous les cas. Il semble
done que, lorsque des maxima d'ordre courts se surcedent, leur processus
de formation a tendance a s'accelerer. L'etude approfondie de ce
phenomene reste a faire, mais on note que les distributions de mv max, l
max et E sont sensiblement les memes pour les maxima d'ordre C alternes
avec des maxima d'ordre L et pour des maxima C formant une serie.
ANALYSE CHRONOLOGIQUE DES VARIATIONS LUMINEUSES
Nous avons utilise quatre methodes d'etude, que voici:
1. Les chaines de Markov
Considerons une suite chronologique d'etats E, observes a des instants
t, tels que l'on ait E(i1, t1), E(i2, t2) ... E(in, tn) ou i = 1, 2, ... n.
Par definition, une telle suite obeit a une chaine de Markov simple si, quels que soient
n et j, la probabilite d'observer un etat donne E(j) a l'instant tn + 1 ne depend
que de l'etat precedent E (in, tn) et non pas des etats anterieurs.
L'observation permet d'etablir une matrice carree d'ordre r, dite matrice
de transition |PK|
La probabilite P[E(j,tn+1)/E(in, tn)] est appelee probabilite de
transition en une epreuve. Elle est representee par une matrice [P1](ou k = 1).
On peut aussi calculer des matrices de transition en p epreuves, pour
lesquelles:
P[E(j, tn+1)/E(i, tn-p+1)] = [P1]pj
Dans la pratique on calcule des matrices de transition en deux et trois
epreuves, [P2] et [P3] et on les compare avee le carre et le cube de la
matrice [P1] observee.
Si l'on a:
[P1]2~=[P2]
[P1]2~=[P3]
(relation de Chapman-Kolmogorov) c'est que les maxima evoluent suivant
une chaine de Markov simple: la nature d'un maximum depend alors du maximum
precedent et seulement de celui-ci.
Martel (1961) avait signale que c'est le cas de SS Cygni, mais Mme Lortet
(1964, 1966) appliquant divers tests sur le caractere aleatoire d'une serie de
deux ou trois parametres, arrive aux conclusions suivantes:
- la succession des maxima de caractere long et non-long est assez
bien representee par une chaine de Markov d'ordre 1, mais notons que SS Cygni
a une nette tendance a l'alternance reguliere des deux types, ce qui
n'est pas le cas de toutes les etoiles que nous avons etudie.
- la succession des maxima faibles (F) et non faibles peut se representer
par une chaine de Markov d'ordre 2.
- un schema markovien d'ordre 1, 2 ou plus n'explique pas l'existance
des series de maxima courts, ou des periodes erratiques, riches en variations
irregulieres.
Mme Lortet a donc propose un schema d'evenement recurrent ou les structures
successives sont independantes, ont chacune une certaine probabilite, et
ou l'evenement est constitute par un changement de structure. Ces structures
cycliques peuvent etre, soit les suites long-court, les suites
court-court et les variations non normales (oscillations, paliers, etc ...).
Pour plusieurs etoiles, Menager et moi avons applique deux tests, l'un
en calculant des matrices theoriques normalisees, et en appliquant a ces
matrices normalisees |Pk| un test en chi2 des transitions en une epreuve, l'autre
en calculant des matrices [P1]2 et [P1]3, deduites de [P1], malgre la
difficulte de leur attribuer un intervalle de confiance, et en les
comparant aux matrices [P2] et [P3].
Les resultats obtenus sont resumes par le tableau suivant:
Variables m chi[P2] P(chi2>chi02) chi[P3] P(chi2>chi02) Auteur
SS Aur 4 11,54 0,02 5,19 0,25 (7)
Z Cam 1 5,30 0,025 Menager
U Gem 1 10,8 0,01 4,7 0,16 Petit
VW Hyi 1 3,44 0,07 3,2 0,08 Menager
CN Ori 1 4,7 0,04 Petit
Dans tous les cas il n'apparait pas que l'on soit devant une chain de
Markov simple.
2. La fonction d'autocorrelation
Il faut remarquer que la suite des intervalles peut etre markovienne
sans que la suite des maxima le soit. Menager a repris l'analyse, en
calculant une fonction d'autocorrelation, ou le coefficient
d'autocorrelation r(p) est defini par:
Une telle analyse a ete faite pour six etoiles (tableau suivant);
Lorsque est positif, les evenements A et B ont tendance a se grouper,
quand t este negativ, ils ont tendance a alterner
Etoiles R_0 sigma(R) t P(t>t0) Auteur
SS Aur 32,1 3,3 -3,7 0,0001 Menager
Z Cam 23 2,4 4,1 0,00002 Menager
U Gem 53,2 5,5 3,3 0,0001 Petit
VW Hyi 42,9 4,1 2,6 0,009 Menager
CN Ori 97 8,5 3,2 0,0001 Petit
TZ Per 45 4,1 3,6 0,0001 Petit
La meme methode permet de mettre en evidence la tendance au groupement
des maxima symetriques, des maxima faibles des oscillations (Lortet,
1964) et d'autres epoques erratiques.
Cette methode a ete aussi utilisee pour l'etude des variations non
normales de deux etoiles du groupe Z Camelopardalis; noun appelons
evenement A les suites variations normales-variations erratiques,
evenement B les suites variations normales-paliers. On obtient:
R_0 sigma(R) t P(t0 > t0)
Z Cam 13,4 1,9 3,9 0,0001
TZ Per 23,5 3,4 3,3 0,001
Menager et Petit (5) ont montre, pour VW Hyi, que pour les series de
maxima d'ordre court, les largeurs des minima sont d'autant plus petites que
le nombre de maxima courts successifs est plus eleve. J'ai verifie ser une
douzaine d'etoiles que ce phenomene existe dans tous les cas. Il semble
done que, lorsque des maxima d'ordre courts se surcedent, leur processus
de formation a tendance a s'accelerer. L'etude approfondie de ce
phenomene reste a faire, mais on note que les distributions de mv max, l
max et E sont sensiblement les memes pour les maxima d'ordre C alternes
avec des maxima d'ordre L et pour des maxima C formant une serie.
ANALYSE CHRONOLOGIQUE DES VARIATIONS LUMINEUSES
Nous avons utilise quatre methodes d'etude, que voici:
1. Les chaines de Markov
Considerons une suite chronologique d'etats E, observes a des instants
t, tels que l'on ait E(i1, t1), E(i2, t2) ... E(in, tn) ou i = 1, 2, ... n.
Par definition, une telle suite obeit a une chaine de Markov simple si, quels que soient
n et j, la probabilite d'observer un etat donne E(j) a l'instant tn + 1 ne depend
que de l'etat precedent E (in, tn) et non pas des etats anterieurs.
L'observation permet d'etablir une matrice carree d'ordre r, dite matrice
de transition |PK|
La probabilite P[E(j,tn+1)/E(in, tn)] est appelee probabilite de
transition en une epreuve. Elle est representee par une matrice [P1](ou k = 1).
On peut aussi calculer des matrices de transition en p epreuves, pour
lesquelles:
P[E(j, tn+1)/E(i, tn-p+1)] = [P1]pj
Dans la pratique on calcule des matrices de transition en deux et trois
epreuves, [P2] et [P3] et on les compare avee le carre et le cube de la
matrice [P1] observee.
Si l'on a:
[P1]2~=[P2]
[P1]2~=[P3]
(relation de Chapman-Kolmogorov) c'est que les maxima evoluent suivant
une chaine de Markov simple: la nature d'un maximum depend alors du maximum
precedent et seulement de celui-ci.
Martel (1961) avait signale que c'est le cas de SS Cygni, mais Mme Lortet
(1964, 1966) appliquant divers tests sur le caractere aleatoire d'une serie de
deux ou trois parametres, arrive aux conclusions suivantes:
- la succession des maxima de caractere long et non-long est assez
bien representee par une chaine de Markov d'ordre 1, mais notons que SS Cygni
a une nette tendance a l'alternance reguliere des deux types, ce qui
n'est pas le cas de toutes les etoiles que nous avons etudie.
- la succession des maxima faibles (F) et non faibles peut se representer
par une chaine de Markov d'ordre 2.
- un schema markovien d'ordre 1, 2 ou plus n'explique pas l'existance
des series de maxima courts, ou des periodes erratiques, riches en variations
irregulieres.
Mme Lortet a donc propose un schema d'evenement recurrent ou les structures
successives sont independantes, ont chacune une certaine probabilite, et
ou l'evenement est constitute par un changement de structure. Ces structures
cycliques peuvent etre, soit les suites long-court, les suites
court-court et les variations non normales (oscillations, paliers, etc ...).
Pour plusieurs etoiles, Menager et moi avons applique deux tests, l'un
en calculant des matrices theoriques normalisees, et en appliquant a ces
matrices normalisees |Pk| un test en chi2 des transitions en une epreuve, l'autre
en calculant des matrices [P1]2 et [P1]3, deduites de [P1], malgre la
difficulte de leur attribuer un intervalle de confiance, et en les
comparant aux matrices [P2] et [P3].
Les resultats obtenus sont resumes par le tableau suivant:
Variables m chi[P2] P(chi2>chi02) chi[P3] P(chi2>chi02) Auteur
SS Aur 4 11,54 0,02 5,19 0,25 (7)
Z Cam 1 5,30 0,025 Menager
U Gem 1 10,8 0,01 4,7 0,16 Petit
VW Hyi 1 3,44 0,07 3,2 0,08 Menager
CN Ori 1 4,7 0,04 Petit
Dans tous les cas il n'apparait pas que l'on soit devant une chain de
Markov simple.
2. La fonction d'autocorrelation
Il faut remarquer que la suite des intervalles peut etre markovienne
sans que la suite des maxima le soit. Menager a repris l'analyse, en
calculant une fonction d'autocorrelation, ou le coefficient
d'autocorrelation r(p) est defini par:
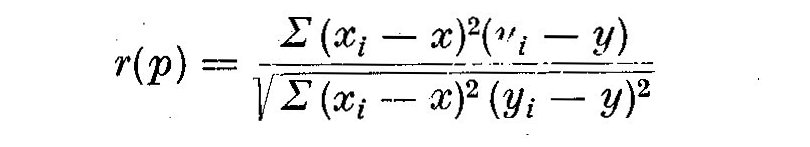 ou p est l'ordre du maximum suivant, et ou
ou p est l'ordre du maximum suivant, et ou
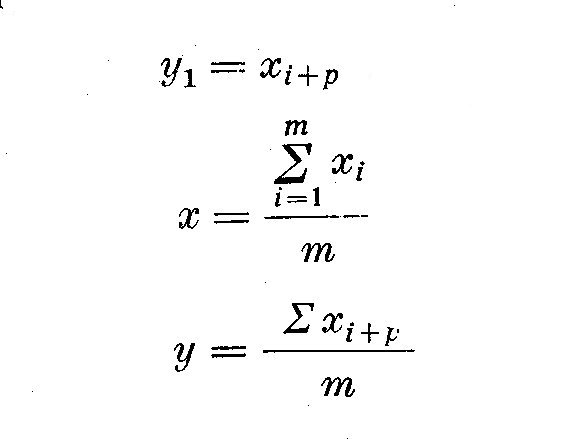 On a
On a
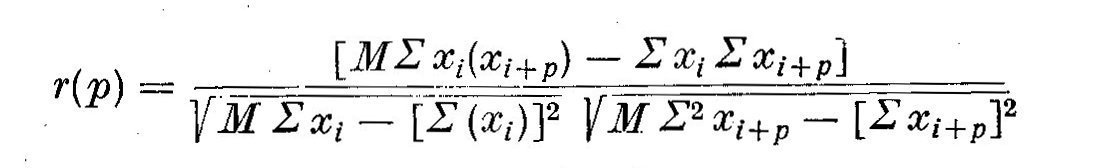 m etant le nombre de termes et N le nombre de couples observes (M = N + p).
On calcule ensuite lea variances en chaque point par
m etant le nombre de termes et N le nombre de couples observes (M = N + p).
On calcule ensuite lea variances en chaque point par
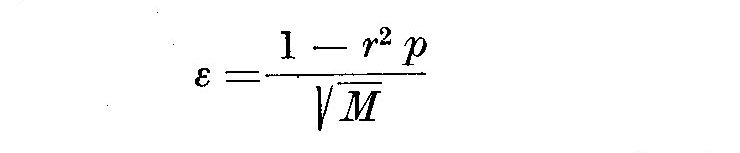 Pour SS Aur et pour Z Cam l'autocorrelogramme des intervalles suggere
une chaine de Markov d'ordre 4 ou plus; pour V W Hyi, la suite des intervalles
semble suivre un processus markovien simple, tandis que la suite des maxima
obeit a un processes d'ordre >=4.
3. Calcul du temps de retour
Le temps de retour est le nombre d'epreuves necessaires pour le retour a
un etat specifie, c'est a dire le nombre theorique de suites long-non long
que l'on compare ensuite aux nombres observes.
Pour Z Cam on observe, par rapport au calcul d'une matrice theorique,
un deficit de transition pour les suites de maxima courts d'ordre 1, ou d'ordre
>4, et un exces de transition pour les valeurs moyennes.
On conclut que lea suites de maxima longs suivent un schema conforme
a celui de la matrice [P1] en une epreuve, tandis que les suites de maxima
courts se rapprochent du schema d'un tirage exhaustif d'evenements A et B
absolument aleatoires.
4. Test de recurrence
Cette methode a ete utilisee pour l'analyse des l min. On pose
Pour SS Aur et pour Z Cam l'autocorrelogramme des intervalles suggere
une chaine de Markov d'ordre 4 ou plus; pour V W Hyi, la suite des intervalles
semble suivre un processus markovien simple, tandis que la suite des maxima
obeit a un processes d'ordre >=4.
3. Calcul du temps de retour
Le temps de retour est le nombre d'epreuves necessaires pour le retour a
un etat specifie, c'est a dire le nombre theorique de suites long-non long
que l'on compare ensuite aux nombres observes.
Pour Z Cam on observe, par rapport au calcul d'une matrice theorique,
un deficit de transition pour les suites de maxima courts d'ordre 1, ou d'ordre
>4, et un exces de transition pour les valeurs moyennes.
On conclut que lea suites de maxima longs suivent un schema conforme
a celui de la matrice [P1] en une epreuve, tandis que les suites de maxima
courts se rapprochent du schema d'un tirage exhaustif d'evenements A et B
absolument aleatoires.
4. Test de recurrence
Cette methode a ete utilisee pour l'analyse des l min. On pose
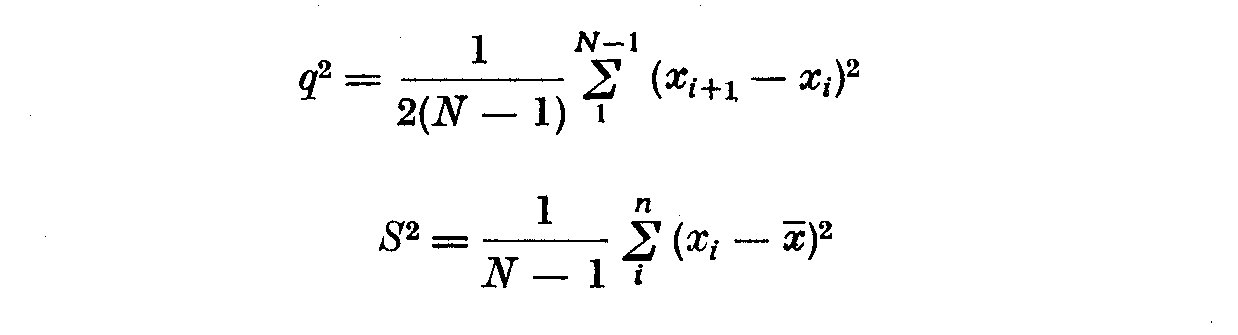 q2 etant la variance de 2 valeurs successives de la variable x et S2 la
variance de x. Soit
q2 etant la variance de 2 valeurs successives de la variable x et S2 la
variance de x. Soit
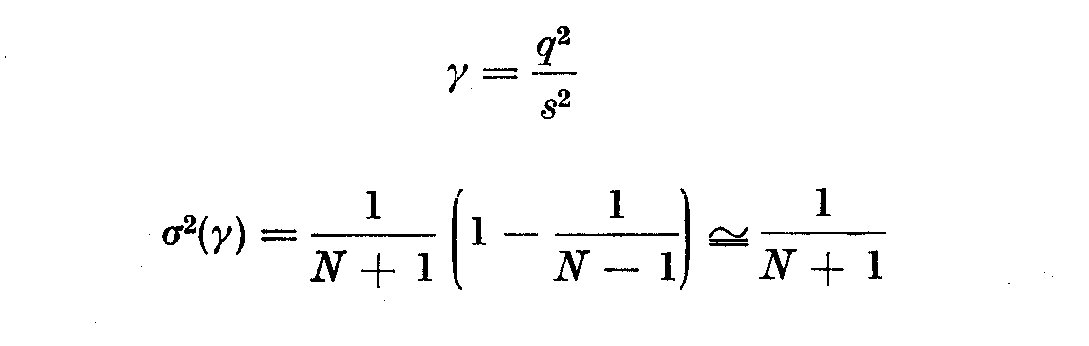 Pour Z Cam on obtient q2 = 25, S2 = 36,2 gamma = 0,69. Le test de Student
nous donne:
t = 1-gamma/sigma gamma = 5.1 p(t>t0)<10^-6
ce qui indique une tendance a la recurrence. Les calculs effectues sur SS Aur
et U Gem confirment ce phenomene; dans ces deux cas p(t>t0)<10^-5.
Ainsi notre analyse confirme qu'un schema de chaine markovienne, s'il
suffit dans certains cas, a l'etude de la succession des intervalles n'explique
ni la tendance au groupement des maxima faibles ou symetriques, ni l'existence
de periodes erratiques diverses. Il semble donc preferable d'adopter un
schema d'evenement recurrent, mais une analyse complete demandera de disposer
de series de maxima longues et continues et d'une bonne classification
des phenomenes observes.
REFERENCES
Campbell, L., 1933, Ann. Harv. Coll. Obs., 90, No. 3.
Lortet-Zuckermann, M. C., 1964, Ann. Astrophys. 27, 65.
Lortet-Zuckermann, M. C., 1966, Ann. Astrophys. 29, 205.
Martel, L., 1961, Ann. Astrophys. 24, 267.
Menager, L. et Petit, M., (a paraitre).
Petit, M. et Menager, L., 1963, Ciel Terre 79, 407.
Zuckermann, M. C., 1961, Ann. Astrophys. 24, 431.
Pour Z Cam on obtient q2 = 25, S2 = 36,2 gamma = 0,69. Le test de Student
nous donne:
t = 1-gamma/sigma gamma = 5.1 p(t>t0)<10^-6
ce qui indique une tendance a la recurrence. Les calculs effectues sur SS Aur
et U Gem confirment ce phenomene; dans ces deux cas p(t>t0)<10^-5.
Ainsi notre analyse confirme qu'un schema de chaine markovienne, s'il
suffit dans certains cas, a l'etude de la succession des intervalles n'explique
ni la tendance au groupement des maxima faibles ou symetriques, ni l'existence
de periodes erratiques diverses. Il semble donc preferable d'adopter un
schema d'evenement recurrent, mais une analyse complete demandera de disposer
de series de maxima longues et continues et d'une bonne classification
des phenomenes observes.
REFERENCES
Campbell, L., 1933, Ann. Harv. Coll. Obs., 90, No. 3.
Lortet-Zuckermann, M. C., 1964, Ann. Astrophys. 27, 65.
Lortet-Zuckermann, M. C., 1966, Ann. Astrophys. 29, 205.
Martel, L., 1961, Ann. Astrophys. 24, 267.
Menager, L. et Petit, M., (a paraitre).
Petit, M. et Menager, L., 1963, Ciel Terre 79, 407.
Zuckermann, M. C., 1961, Ann. Astrophys. 24, 431.