Non-Periodic Phenomena in Variable Stars
IAU Colloquium, Budapest, 1968
ON A POSSIBLE CAUSE OF BRIGHTNESS FLUCTUATIONS IN
CLOSE BINARY SYSTEMS OF DWARF STARS
by V. G. GORBATZKY
Leningrad University Observatory, USSR.
The observational data on novae, recurrent novae and U Gem stars
recently obtained (Kraft, 1963) show that most of these stars and very
likely all of them are binary systems. They consist of dwarf stars and
some of these systems are observed as eclipsing ones. In this case the
light curve of the system has the following peculiarities:
1. Short periods, usually near to 6h.
2. The primary light minimum is asymmetrical.
3. The secondary light minimum is very shallow or unobservable.
4. Brightness fluctuations, superposed on the eclipse light curve, are
observed. Their amplitude is about 0.05m and their time scale is of the
order of 1 min. The fluctuations are more outstanding near the phase
0.25 P and before the primary light minimum. They are smallest on the
descending branch to the light minimum.
A possible explanation of these brightness fluctuations is proposed in
this note. As it is well known from spectroscopic observations, the
primaries of the close binaries of the type considered here have
disk-like gaseous envelopes. It was found from theoretical study of gas
motions in a close system of two gravitating points (Prendergast, 1960),
that in the vicinity of each point these motions differ only a little
from the circular Keplerian ones. Consequently, an azimuthal velocity
gradient must exist in the disk-like envelope.
The flow of gas in the envelope towards the stellar surface is caused by
turbulent viscosity. If there is no permanent supply of gas, the
envelope will vanish. All the matter it contains will join the star.
Estimates show (Gorbatzky, 1968) that this will occur within one day or
even at a shorter time. However, we observe the envelopes over long time
intervals, and this must be considered as an evidence of the supply of
the envelopes with gas. This supply may be realized only by gaseous
streams flowing from the other star of the binary system. In the case of
WZ Sge the stream ("jet") that transfers the matter to the envelope of
the primary star, can be detected directly (Krzeminsky and Kraft, 1964)
by spectroscopic observations.
The gaseous jet must be accelerated by the star's gravitational field.
If the initial velocity of the gas is small enough, its radial velocity
v near the envelope is of the order
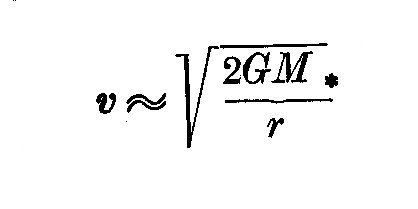 (1)
Taking the mass of the star M_*~~M_Sun, and the radius of the envelope
r~~10^10 cm, as found from observations, we get v~5*10^7 cm sec^-1.
A more precise calculation, making allowance for the gas pressure as well
as for the effects caused by the rotation of the stars around their
common center of gravity, leads to values of V of the same order.
The disk-like envelope emits the radiation not only in discrete
frequencies but also in the continuum. As it may be inferred from
photometric data, the brightness of the system diminishes substantially
even during the eclipse of the envelope. Consequently, the observable
continuous radiation of the envelope is significant, sometimes it may
give the main contribution to the total radiation of the system.
The kinetic energy of the gas flowing into the envelope must be one of
the main sources of the radiation emitted by the envelope. The heated region is
formed at the place where the gas flow encounters the envelope. The radiation
of this region is more intense than that of the other parts of the envelope.
Apparently just in this place we observe the so called "hot spot", the
presence of which has been supposed in some studies to explain the
peculiarities of the light curve. The "shoulder" on the light curve that
precedes the primary minimum corresponds to phases of best visibility of
the spot. During this light minimum the hot spot is eclipsed by the cold
secondary star.
The calculations show that almost half of the total kinetic energy of
the gaseous streams will be transformed into the radiation of the hot
spot region (the rest of the energy dissipates in other regions of the
envelope later). Hence the energy E radiated by the envelope is
(1)
Taking the mass of the star M_*~~M_Sun, and the radius of the envelope
r~~10^10 cm, as found from observations, we get v~5*10^7 cm sec^-1.
A more precise calculation, making allowance for the gas pressure as well
as for the effects caused by the rotation of the stars around their
common center of gravity, leads to values of V of the same order.
The disk-like envelope emits the radiation not only in discrete
frequencies but also in the continuum. As it may be inferred from
photometric data, the brightness of the system diminishes substantially
even during the eclipse of the envelope. Consequently, the observable
continuous radiation of the envelope is significant, sometimes it may
give the main contribution to the total radiation of the system.
The kinetic energy of the gas flowing into the envelope must be one of
the main sources of the radiation emitted by the envelope. The heated region is
formed at the place where the gas flow encounters the envelope. The radiation
of this region is more intense than that of the other parts of the envelope.
Apparently just in this place we observe the so called "hot spot", the
presence of which has been supposed in some studies to explain the
peculiarities of the light curve. The "shoulder" on the light curve that
precedes the primary minimum corresponds to phases of best visibility of
the spot. During this light minimum the hot spot is eclipsed by the cold
secondary star.
The calculations show that almost half of the total kinetic energy of
the gaseous streams will be transformed into the radiation of the hot
spot region (the rest of the energy dissipates in other regions of the
envelope later). Hence the energy E radiated by the envelope is
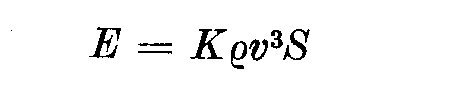 (2)
Here rho is the gas density, v the gas velocity, K is a coefficient of
the order of unity.
In theoretical studies the gaseous stream is usually considered as a
continuous jet flowing from point L_1 and having constant velocity and
constant capacity. The envelope is assumed to be a homogeneous disk.
There are no observational data which confirm the validity of such a
simple model. On the contrary, the observed differences in the depths of
light minima in different cycles are evidences of rapid changes in the
dimensions of the envelope. Hence the capacity of the gaseous flow also
changes. Variations in the velocity of the jet are observed in case of
WZ Sge.
A variation of not more than 10 per cent in the density of the jet, or a
change of a few per cent in the velocity of the gaseous streams is sufficient
to change the luminosity of the envelope by about ten per cent and,
correspondingly, the brightness of the system changes by several hundredths
of a magnitude. Apparently, inhomogeneity of the jet on such a scale is quite
possible and it may be the main cause of the observed brightness fluctuations.
The stream seems to flow out from its envelope and not from the
secondary star. There are spectroscopic evidences of the presence of
envelopes around the cool secondaries (Greenstein, 1960). Since well
developed turbulence must exist in such an envelope, the stream flowing
out from it cannot be fully homogeneous. The scale of inhomogeneities in
the stream and in the envelope must be of the same order.
If the brightness fluctuations are caused by inhomogeneity of the
gaseous stream, one can estimate the size d of the largest inhomogeneities in
the envelope of the secondary star. Using data on the duration (Delta t) of
the brightness fluctuations and taking into account that d ~ v Delta t,
we find that d is of the order of 10^9 cm. On the other hand, we have
earlier estimated (Gorbatzky, 1965) the scale (l) of the turbulence in a
disk-like envelope. It can be found from the equation, that
(2)
Here rho is the gas density, v the gas velocity, K is a coefficient of
the order of unity.
In theoretical studies the gaseous stream is usually considered as a
continuous jet flowing from point L_1 and having constant velocity and
constant capacity. The envelope is assumed to be a homogeneous disk.
There are no observational data which confirm the validity of such a
simple model. On the contrary, the observed differences in the depths of
light minima in different cycles are evidences of rapid changes in the
dimensions of the envelope. Hence the capacity of the gaseous flow also
changes. Variations in the velocity of the jet are observed in case of
WZ Sge.
A variation of not more than 10 per cent in the density of the jet, or a
change of a few per cent in the velocity of the gaseous streams is sufficient
to change the luminosity of the envelope by about ten per cent and,
correspondingly, the brightness of the system changes by several hundredths
of a magnitude. Apparently, inhomogeneity of the jet on such a scale is quite
possible and it may be the main cause of the observed brightness fluctuations.
The stream seems to flow out from its envelope and not from the
secondary star. There are spectroscopic evidences of the presence of
envelopes around the cool secondaries (Greenstein, 1960). Since well
developed turbulence must exist in such an envelope, the stream flowing
out from it cannot be fully homogeneous. The scale of inhomogeneities in
the stream and in the envelope must be of the same order.
If the brightness fluctuations are caused by inhomogeneity of the
gaseous stream, one can estimate the size d of the largest inhomogeneities in
the envelope of the secondary star. Using data on the duration (Delta t) of
the brightness fluctuations and taking into account that d ~ v Delta t,
we find that d is of the order of 10^9 cm. On the other hand, we have
earlier estimated (Gorbatzky, 1965) the scale (l) of the turbulence in a
disk-like envelope. It can be found from the equation, that
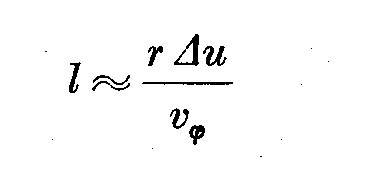 (3)
where Delta u is the velocity of the turbulent pulsations and v_phi is the
azimuthal velocity. The value of Delta u cannot be higher than some tens of
km/sec and v_phi~~5.10^7 cm/sec. Therefore, taking r~~10^10 cm we
have l <= 10^9 cm. In this way we found that the size of inhomogeneities in the
envelope of the secondary star and correspondingly the scale of non-uniformity
in the stream are of the same order as the main scale of turbulent motions in
the envelope. The turbulence in the envelope of the secondary star can result
in inhomogeneity of the gaseous jet flowing into the envelope of the primary.
The fact, that d~~l, seems to confirm our assumption on the cause of brightness
fluctuations in close binary systems of dwarf stars.
The inhomogeneity of the stream combined with the rotation of the
envelope makes the envelope structure rather complex. Densities in the
envelope in the same distance from the primary star may be different.
This must result in different emissivity. As the envelope rotates, this
may also cause brightness fluctuations. In both cases changes in the
capacity of a gaseous flow give rise to brightness fluctuations in the
systems considered.
REFERENCES
Gorbatzky, V. G., 1965, Trudy astr. Obs. Leningr. gos. Univ. 23, 15.
Gorbatzky, V. G., 1968, Report Trieste Symp. (in press).
Greenstein, J. L., 1960, Stellar Atmospheres, ed. by J. L. Greenstein
(Univ. of Chicago Press. Ch. 19).
Kraft, R., 1963, Cataclysmic Variables as Binary Stars. Adv. Astr. Astrophys. 2, p. 43.
Krzeminsky, W. and Kraft, R., 1964, Astrophys. J., 140, 921.
Prendergast, K., 1960, Astrophys. J., 132, 162.
(3)
where Delta u is the velocity of the turbulent pulsations and v_phi is the
azimuthal velocity. The value of Delta u cannot be higher than some tens of
km/sec and v_phi~~5.10^7 cm/sec. Therefore, taking r~~10^10 cm we
have l <= 10^9 cm. In this way we found that the size of inhomogeneities in the
envelope of the secondary star and correspondingly the scale of non-uniformity
in the stream are of the same order as the main scale of turbulent motions in
the envelope. The turbulence in the envelope of the secondary star can result
in inhomogeneity of the gaseous jet flowing into the envelope of the primary.
The fact, that d~~l, seems to confirm our assumption on the cause of brightness
fluctuations in close binary systems of dwarf stars.
The inhomogeneity of the stream combined with the rotation of the
envelope makes the envelope structure rather complex. Densities in the
envelope in the same distance from the primary star may be different.
This must result in different emissivity. As the envelope rotates, this
may also cause brightness fluctuations. In both cases changes in the
capacity of a gaseous flow give rise to brightness fluctuations in the
systems considered.
REFERENCES
Gorbatzky, V. G., 1965, Trudy astr. Obs. Leningr. gos. Univ. 23, 15.
Gorbatzky, V. G., 1968, Report Trieste Symp. (in press).
Greenstein, J. L., 1960, Stellar Atmospheres, ed. by J. L. Greenstein
(Univ. of Chicago Press. Ch. 19).
Kraft, R., 1963, Cataclysmic Variables as Binary Stars. Adv. Astr. Astrophys. 2, p. 43.
Krzeminsky, W. and Kraft, R., 1964, Astrophys. J., 140, 921.
Prendergast, K., 1960, Astrophys. J., 132, 162.
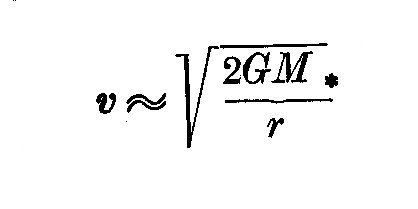 (1)
Taking the mass of the star M_*~~M_Sun, and the radius of the envelope
r~~10^10 cm, as found from observations, we get v~5*10^7 cm sec^-1.
A more precise calculation, making allowance for the gas pressure as well
as for the effects caused by the rotation of the stars around their
common center of gravity, leads to values of V of the same order.
The disk-like envelope emits the radiation not only in discrete
frequencies but also in the continuum. As it may be inferred from
photometric data, the brightness of the system diminishes substantially
even during the eclipse of the envelope. Consequently, the observable
continuous radiation of the envelope is significant, sometimes it may
give the main contribution to the total radiation of the system.
The kinetic energy of the gas flowing into the envelope must be one of
the main sources of the radiation emitted by the envelope. The heated region is
formed at the place where the gas flow encounters the envelope. The radiation
of this region is more intense than that of the other parts of the envelope.
Apparently just in this place we observe the so called "hot spot", the
presence of which has been supposed in some studies to explain the
peculiarities of the light curve. The "shoulder" on the light curve that
precedes the primary minimum corresponds to phases of best visibility of
the spot. During this light minimum the hot spot is eclipsed by the cold
secondary star.
The calculations show that almost half of the total kinetic energy of
the gaseous streams will be transformed into the radiation of the hot
spot region (the rest of the energy dissipates in other regions of the
envelope later). Hence the energy E radiated by the envelope is
(1)
Taking the mass of the star M_*~~M_Sun, and the radius of the envelope
r~~10^10 cm, as found from observations, we get v~5*10^7 cm sec^-1.
A more precise calculation, making allowance for the gas pressure as well
as for the effects caused by the rotation of the stars around their
common center of gravity, leads to values of V of the same order.
The disk-like envelope emits the radiation not only in discrete
frequencies but also in the continuum. As it may be inferred from
photometric data, the brightness of the system diminishes substantially
even during the eclipse of the envelope. Consequently, the observable
continuous radiation of the envelope is significant, sometimes it may
give the main contribution to the total radiation of the system.
The kinetic energy of the gas flowing into the envelope must be one of
the main sources of the radiation emitted by the envelope. The heated region is
formed at the place where the gas flow encounters the envelope. The radiation
of this region is more intense than that of the other parts of the envelope.
Apparently just in this place we observe the so called "hot spot", the
presence of which has been supposed in some studies to explain the
peculiarities of the light curve. The "shoulder" on the light curve that
precedes the primary minimum corresponds to phases of best visibility of
the spot. During this light minimum the hot spot is eclipsed by the cold
secondary star.
The calculations show that almost half of the total kinetic energy of
the gaseous streams will be transformed into the radiation of the hot
spot region (the rest of the energy dissipates in other regions of the
envelope later). Hence the energy E radiated by the envelope is
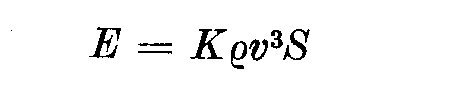 (2)
Here rho is the gas density, v the gas velocity, K is a coefficient of
the order of unity.
In theoretical studies the gaseous stream is usually considered as a
continuous jet flowing from point L_1 and having constant velocity and
constant capacity. The envelope is assumed to be a homogeneous disk.
There are no observational data which confirm the validity of such a
simple model. On the contrary, the observed differences in the depths of
light minima in different cycles are evidences of rapid changes in the
dimensions of the envelope. Hence the capacity of the gaseous flow also
changes. Variations in the velocity of the jet are observed in case of
WZ Sge.
A variation of not more than 10 per cent in the density of the jet, or a
change of a few per cent in the velocity of the gaseous streams is sufficient
to change the luminosity of the envelope by about ten per cent and,
correspondingly, the brightness of the system changes by several hundredths
of a magnitude. Apparently, inhomogeneity of the jet on such a scale is quite
possible and it may be the main cause of the observed brightness fluctuations.
The stream seems to flow out from its envelope and not from the
secondary star. There are spectroscopic evidences of the presence of
envelopes around the cool secondaries (Greenstein, 1960). Since well
developed turbulence must exist in such an envelope, the stream flowing
out from it cannot be fully homogeneous. The scale of inhomogeneities in
the stream and in the envelope must be of the same order.
If the brightness fluctuations are caused by inhomogeneity of the
gaseous stream, one can estimate the size d of the largest inhomogeneities in
the envelope of the secondary star. Using data on the duration (Delta t) of
the brightness fluctuations and taking into account that d ~ v Delta t,
we find that d is of the order of 10^9 cm. On the other hand, we have
earlier estimated (Gorbatzky, 1965) the scale (l) of the turbulence in a
disk-like envelope. It can be found from the equation, that
(2)
Here rho is the gas density, v the gas velocity, K is a coefficient of
the order of unity.
In theoretical studies the gaseous stream is usually considered as a
continuous jet flowing from point L_1 and having constant velocity and
constant capacity. The envelope is assumed to be a homogeneous disk.
There are no observational data which confirm the validity of such a
simple model. On the contrary, the observed differences in the depths of
light minima in different cycles are evidences of rapid changes in the
dimensions of the envelope. Hence the capacity of the gaseous flow also
changes. Variations in the velocity of the jet are observed in case of
WZ Sge.
A variation of not more than 10 per cent in the density of the jet, or a
change of a few per cent in the velocity of the gaseous streams is sufficient
to change the luminosity of the envelope by about ten per cent and,
correspondingly, the brightness of the system changes by several hundredths
of a magnitude. Apparently, inhomogeneity of the jet on such a scale is quite
possible and it may be the main cause of the observed brightness fluctuations.
The stream seems to flow out from its envelope and not from the
secondary star. There are spectroscopic evidences of the presence of
envelopes around the cool secondaries (Greenstein, 1960). Since well
developed turbulence must exist in such an envelope, the stream flowing
out from it cannot be fully homogeneous. The scale of inhomogeneities in
the stream and in the envelope must be of the same order.
If the brightness fluctuations are caused by inhomogeneity of the
gaseous stream, one can estimate the size d of the largest inhomogeneities in
the envelope of the secondary star. Using data on the duration (Delta t) of
the brightness fluctuations and taking into account that d ~ v Delta t,
we find that d is of the order of 10^9 cm. On the other hand, we have
earlier estimated (Gorbatzky, 1965) the scale (l) of the turbulence in a
disk-like envelope. It can be found from the equation, that
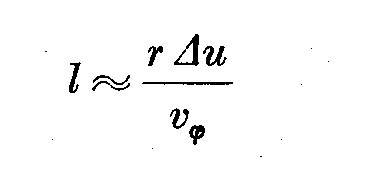 (3)
where Delta u is the velocity of the turbulent pulsations and v_phi is the
azimuthal velocity. The value of Delta u cannot be higher than some tens of
km/sec and v_phi~~5.10^7 cm/sec. Therefore, taking r~~10^10 cm we
have l <= 10^9 cm. In this way we found that the size of inhomogeneities in the
envelope of the secondary star and correspondingly the scale of non-uniformity
in the stream are of the same order as the main scale of turbulent motions in
the envelope. The turbulence in the envelope of the secondary star can result
in inhomogeneity of the gaseous jet flowing into the envelope of the primary.
The fact, that d~~l, seems to confirm our assumption on the cause of brightness
fluctuations in close binary systems of dwarf stars.
The inhomogeneity of the stream combined with the rotation of the
envelope makes the envelope structure rather complex. Densities in the
envelope in the same distance from the primary star may be different.
This must result in different emissivity. As the envelope rotates, this
may also cause brightness fluctuations. In both cases changes in the
capacity of a gaseous flow give rise to brightness fluctuations in the
systems considered.
REFERENCES
Gorbatzky, V. G., 1965, Trudy astr. Obs. Leningr. gos. Univ. 23, 15.
Gorbatzky, V. G., 1968, Report Trieste Symp. (in press).
Greenstein, J. L., 1960, Stellar Atmospheres, ed. by J. L. Greenstein
(Univ. of Chicago Press. Ch. 19).
Kraft, R., 1963, Cataclysmic Variables as Binary Stars. Adv. Astr. Astrophys. 2, p. 43.
Krzeminsky, W. and Kraft, R., 1964, Astrophys. J., 140, 921.
Prendergast, K., 1960, Astrophys. J., 132, 162.
(3)
where Delta u is the velocity of the turbulent pulsations and v_phi is the
azimuthal velocity. The value of Delta u cannot be higher than some tens of
km/sec and v_phi~~5.10^7 cm/sec. Therefore, taking r~~10^10 cm we
have l <= 10^9 cm. In this way we found that the size of inhomogeneities in the
envelope of the secondary star and correspondingly the scale of non-uniformity
in the stream are of the same order as the main scale of turbulent motions in
the envelope. The turbulence in the envelope of the secondary star can result
in inhomogeneity of the gaseous jet flowing into the envelope of the primary.
The fact, that d~~l, seems to confirm our assumption on the cause of brightness
fluctuations in close binary systems of dwarf stars.
The inhomogeneity of the stream combined with the rotation of the
envelope makes the envelope structure rather complex. Densities in the
envelope in the same distance from the primary star may be different.
This must result in different emissivity. As the envelope rotates, this
may also cause brightness fluctuations. In both cases changes in the
capacity of a gaseous flow give rise to brightness fluctuations in the
systems considered.
REFERENCES
Gorbatzky, V. G., 1965, Trudy astr. Obs. Leningr. gos. Univ. 23, 15.
Gorbatzky, V. G., 1968, Report Trieste Symp. (in press).
Greenstein, J. L., 1960, Stellar Atmospheres, ed. by J. L. Greenstein
(Univ. of Chicago Press. Ch. 19).
Kraft, R., 1963, Cataclysmic Variables as Binary Stars. Adv. Astr. Astrophys. 2, p. 43.
Krzeminsky, W. and Kraft, R., 1964, Astrophys. J., 140, 921.
Prendergast, K., 1960, Astrophys. J., 132, 162.