Non-Periodic Phenomena in Variable Stars
IAU Colloquium, Budapest, 1968
THEORETICAL LIGHT CHANGES OF W UMa STARS WITH LOW
MASS RATIO
H. MAUDER
Remeis Sternwarte, Bamberg, Germany
The main obstacle in calculating reliable elements for W UMa-stars is
due to the fact that these stars are highly distorted. Therefore one
should carefully take into account the influence of distortion on the
light curves of these stars. Usually this is done by a rectification
process which transforms the observed light curve to the equivalent
light curve of a pair of spherical stars. There are two assumptions that
make this process inadequate in the case of very close binaries. The
first assumption is that both stars are ellipsoidals of equal shape. The
second assumption is following from the first, namely that it should be
possible to extrapolate the light changes of the rotating deformed stars
which are observable outside the eclipses to the whole cycle and
especially to the minima.
At the last Colloquium on variable stars at Bamberg in 1965 Binnendijk
presented a paper on W UMa stars. It was impossible to derive elements
for the first four systems he had shown. This is due not only to the
shallowness of the eclipses but to another effect. One should take
attention of the fact that there is a remarkable change of light outside
the eclipses and a large period of constant brightness during secondary
minimum, especially in the case of AW UMa. This star was observed by
Paczynski and later on by Kalish who confirmed this effect. Any
rectification based on the light changes outside the eclipses will lead
to a rectified light curve which cannot be attributed to any pair of
spheroidal stars. In Fig. 1 one can see a fairly trustworthy primary
minimum and a totally unfamiliar secondary minimum. Reaching the
secondary minimum the star brightens, then decreases a little in brightness
and than shows a large hump around the middle of the minimum that makes the
system actually brighter than its rectified maximum brightness. This effect
is present though less pronounced in the case of the other three stars, too.
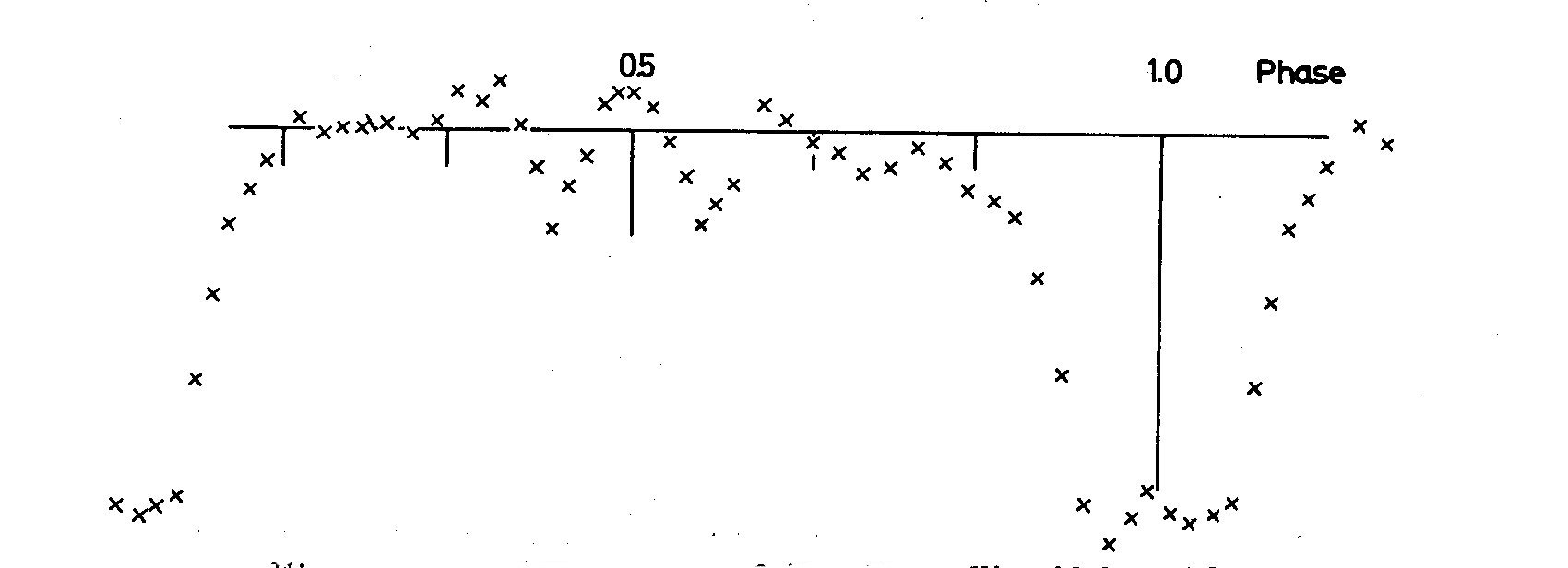 Fig. 1. Rectified light curve of AW UMa, ellipsoidal model
Fig. 1. Rectified light curve of AW UMa, ellipsoidal model
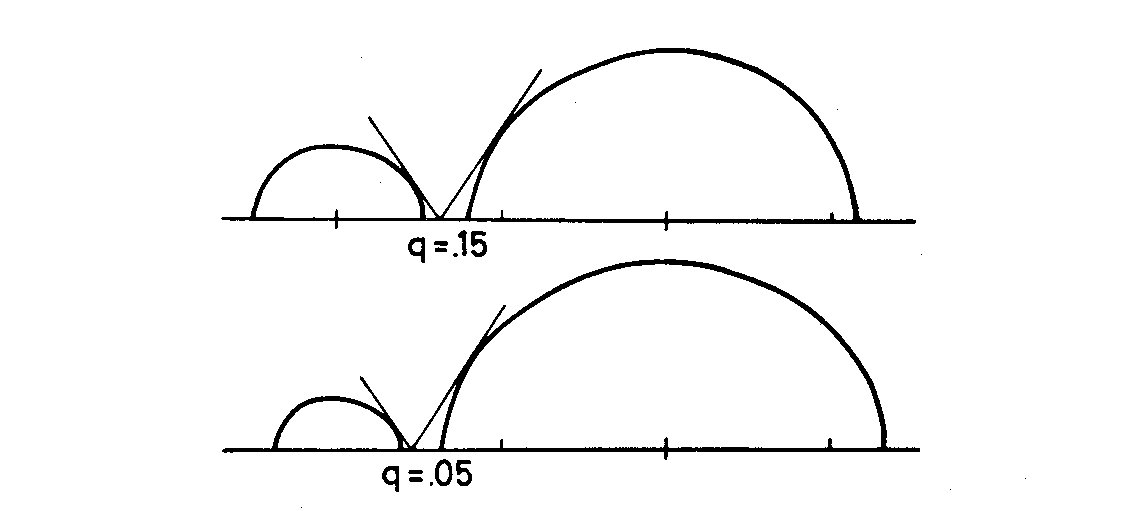 Fig. 2. Model for contact binaries with low mass ratio q
To understand the behaviour of these stars theoretical light changes
were calculated for a pair of stars which are actually in contact, that means,
they are filling their critical Roche lobe. A preliminary analysis had shown
that the systems should have low mass ratio, less than 0.20. It was tried to
find a model that represents satisfactorily the actual shape of these stars.
It was checked numerically that the critical Roche lobe can be approximated
by a three-axial ellipsoid combined with a cone whose top is at the inner
Lagrangian point and which osculates the ellipsoid. (Fig. 2). The straight line
in the figure is not the osculating cone but the tangent to the Roche lobe at
the inner Lagrangian point. The difference against the osculating cone is too
small to be drawn. Numerically the difference between the model and the
apparent Roche lobe for this small values of the mass ratio is less than 0.2
per cent of the radius for the smaller component and less than 0.5 per cent
of the radius for the larger one. Calculating the light changes of this
configuration, one finds the following (see Fig. 3). There is a large variation
in brightness outside the eclipse but this variation is much lower when the
eclipse begins. This is due to the fact that just at the onset of the
eclipse the osculating cone is projected directly on the surface of the
eclipsed star and the apparent area of this star - not influenced by
eclipse - is now indeed of an ellipsoidal shape. However, in any
rectification process one extrapolates the straight line of fig. 3 which
leads to a variation in brightness that is much larger than really
present. This causes the rectified minima to be much shallower and even
narrower than they really are, leading to orbital elements you hardly
can trust in. Rectifying according to the postulation that the
brightness of the system not influenced by the eclipses remains constant
leads to the light-curve of Fig. 4. One can see a remarkable difference
in depth and shape of the light curves rectified by a classical method
and by applying the Roche model. However, one should be very cautious
when deriving elements from this light curve. This curve no longer is
due to a spherical model. One can get elements from this curve but these
elements still need corrections.
Fig. 2. Model for contact binaries with low mass ratio q
To understand the behaviour of these stars theoretical light changes
were calculated for a pair of stars which are actually in contact, that means,
they are filling their critical Roche lobe. A preliminary analysis had shown
that the systems should have low mass ratio, less than 0.20. It was tried to
find a model that represents satisfactorily the actual shape of these stars.
It was checked numerically that the critical Roche lobe can be approximated
by a three-axial ellipsoid combined with a cone whose top is at the inner
Lagrangian point and which osculates the ellipsoid. (Fig. 2). The straight line
in the figure is not the osculating cone but the tangent to the Roche lobe at
the inner Lagrangian point. The difference against the osculating cone is too
small to be drawn. Numerically the difference between the model and the
apparent Roche lobe for this small values of the mass ratio is less than 0.2
per cent of the radius for the smaller component and less than 0.5 per cent
of the radius for the larger one. Calculating the light changes of this
configuration, one finds the following (see Fig. 3). There is a large variation
in brightness outside the eclipse but this variation is much lower when the
eclipse begins. This is due to the fact that just at the onset of the
eclipse the osculating cone is projected directly on the surface of the
eclipsed star and the apparent area of this star - not influenced by
eclipse - is now indeed of an ellipsoidal shape. However, in any
rectification process one extrapolates the straight line of fig. 3 which
leads to a variation in brightness that is much larger than really
present. This causes the rectified minima to be much shallower and even
narrower than they really are, leading to orbital elements you hardly
can trust in. Rectifying according to the postulation that the
brightness of the system not influenced by the eclipses remains constant
leads to the light-curve of Fig. 4. One can see a remarkable difference
in depth and shape of the light curves rectified by a classical method
and by applying the Roche model. However, one should be very cautious
when deriving elements from this light curve. This curve no longer is
due to a spherical model. One can get elements from this curve but these
elements still need corrections.
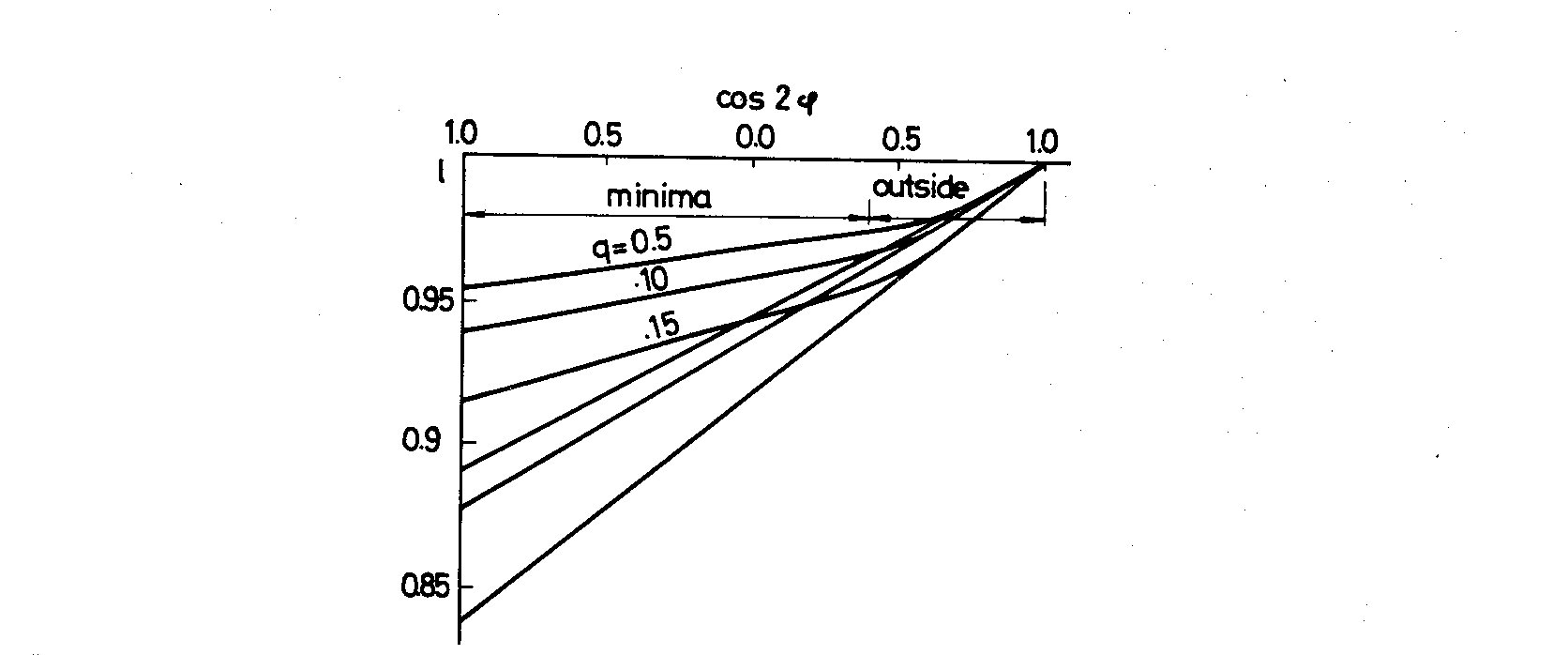 Fig. 3. Light changes for the Roche-model with low mass ratio. The straight
line is the extrapolation of the light changes outside the eclipses
Fig. 3. Light changes for the Roche-model with low mass ratio. The straight
line is the extrapolation of the light changes outside the eclipses
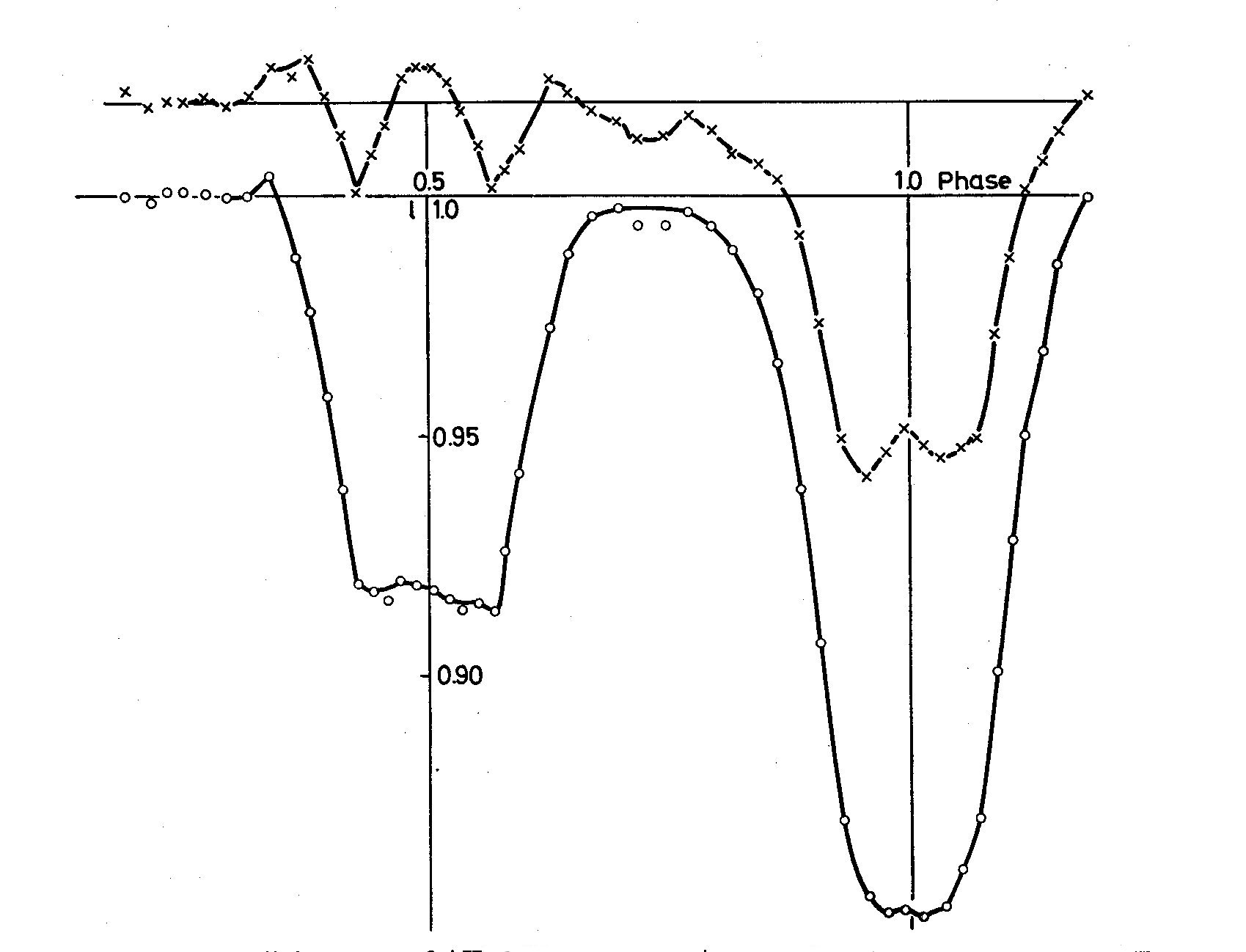 Fig. 4. Rectified light curve of AW UMa according to normal rectification (top)
and by applying the Roche-model (bottom)
There may be a way out of these difficulties. In a previous paper of
the author it was shown that one can get three essentially independent
correlations from the Fourier transform of the total light curve. In the
case of a contact configuration there are three main parameters, namely
the ratio of luminosities, the inclination of the orbit and the mass
ratio, which determines fully the geometrical properties of the system.
Therefore it is to be expected that one can solve the problem by the Fourier
method. However, this possibility is still under numerical examination.
REFERENCES
Binnendijk, L., 1965, Kleine Veroff. Bamberg Nr. 40, p. 36.
Paczynski, B., 1964, Astr. J. 69, p. 124.
Kalish, M. S., 1965, Publ. astr. Soc. Pacific 77, p. 36.
Mauder, H., 1966, Kleine Veroff. Bamberg Nr. 38.
DISCUSSION
Avery: What happens, when the stars do not quite fill the Roche lobes?
Mauder: This is a case much more complicated, for you have two additional
parameters that describe the relative radii of both components beside
the mass ratio. You cannot then solve the problem by the Fourier method
but you are forced to use some other method to solve the light curve.
However, if you use the assumption of a contact configuration you
should check whether the solution fits well with the observed light
curve. If there are differences you should carefully discuss the
possibility of components not filling their respective lobes.
Bakos: How would you treat symmetrical light curves?
Mauder: I would symmetrize the light curve by brute force, for I don't know
a physical process which is so well understood till now that you can
apply it in a universal manner on light curves to produce the
asymmetries observed. I think we should be glad if we succeed to get
reasonable elements for W UMa stars without taking into account the
asymmetries.
Wood: Some of these recent developments in means of rectification are
extremely important and may change substantially some of the data
concerning very close eclipsing systems.
Fig. 4. Rectified light curve of AW UMa according to normal rectification (top)
and by applying the Roche-model (bottom)
There may be a way out of these difficulties. In a previous paper of
the author it was shown that one can get three essentially independent
correlations from the Fourier transform of the total light curve. In the
case of a contact configuration there are three main parameters, namely
the ratio of luminosities, the inclination of the orbit and the mass
ratio, which determines fully the geometrical properties of the system.
Therefore it is to be expected that one can solve the problem by the Fourier
method. However, this possibility is still under numerical examination.
REFERENCES
Binnendijk, L., 1965, Kleine Veroff. Bamberg Nr. 40, p. 36.
Paczynski, B., 1964, Astr. J. 69, p. 124.
Kalish, M. S., 1965, Publ. astr. Soc. Pacific 77, p. 36.
Mauder, H., 1966, Kleine Veroff. Bamberg Nr. 38.
DISCUSSION
Avery: What happens, when the stars do not quite fill the Roche lobes?
Mauder: This is a case much more complicated, for you have two additional
parameters that describe the relative radii of both components beside
the mass ratio. You cannot then solve the problem by the Fourier method
but you are forced to use some other method to solve the light curve.
However, if you use the assumption of a contact configuration you
should check whether the solution fits well with the observed light
curve. If there are differences you should carefully discuss the
possibility of components not filling their respective lobes.
Bakos: How would you treat symmetrical light curves?
Mauder: I would symmetrize the light curve by brute force, for I don't know
a physical process which is so well understood till now that you can
apply it in a universal manner on light curves to produce the
asymmetries observed. I think we should be glad if we succeed to get
reasonable elements for W UMa stars without taking into account the
asymmetries.
Wood: Some of these recent developments in means of rectification are
extremely important and may change substantially some of the data
concerning very close eclipsing systems.
 Fig. 1. Rectified light curve of AW UMa, ellipsoidal model
Fig. 1. Rectified light curve of AW UMa, ellipsoidal model
 Fig. 2. Model for contact binaries with low mass ratio q
To understand the behaviour of these stars theoretical light changes
were calculated for a pair of stars which are actually in contact, that means,
they are filling their critical Roche lobe. A preliminary analysis had shown
that the systems should have low mass ratio, less than 0.20. It was tried to
find a model that represents satisfactorily the actual shape of these stars.
It was checked numerically that the critical Roche lobe can be approximated
by a three-axial ellipsoid combined with a cone whose top is at the inner
Lagrangian point and which osculates the ellipsoid. (Fig. 2). The straight line
in the figure is not the osculating cone but the tangent to the Roche lobe at
the inner Lagrangian point. The difference against the osculating cone is too
small to be drawn. Numerically the difference between the model and the
apparent Roche lobe for this small values of the mass ratio is less than 0.2
per cent of the radius for the smaller component and less than 0.5 per cent
of the radius for the larger one. Calculating the light changes of this
configuration, one finds the following (see Fig. 3). There is a large variation
in brightness outside the eclipse but this variation is much lower when the
eclipse begins. This is due to the fact that just at the onset of the
eclipse the osculating cone is projected directly on the surface of the
eclipsed star and the apparent area of this star - not influenced by
eclipse - is now indeed of an ellipsoidal shape. However, in any
rectification process one extrapolates the straight line of fig. 3 which
leads to a variation in brightness that is much larger than really
present. This causes the rectified minima to be much shallower and even
narrower than they really are, leading to orbital elements you hardly
can trust in. Rectifying according to the postulation that the
brightness of the system not influenced by the eclipses remains constant
leads to the light-curve of Fig. 4. One can see a remarkable difference
in depth and shape of the light curves rectified by a classical method
and by applying the Roche model. However, one should be very cautious
when deriving elements from this light curve. This curve no longer is
due to a spherical model. One can get elements from this curve but these
elements still need corrections.
Fig. 2. Model for contact binaries with low mass ratio q
To understand the behaviour of these stars theoretical light changes
were calculated for a pair of stars which are actually in contact, that means,
they are filling their critical Roche lobe. A preliminary analysis had shown
that the systems should have low mass ratio, less than 0.20. It was tried to
find a model that represents satisfactorily the actual shape of these stars.
It was checked numerically that the critical Roche lobe can be approximated
by a three-axial ellipsoid combined with a cone whose top is at the inner
Lagrangian point and which osculates the ellipsoid. (Fig. 2). The straight line
in the figure is not the osculating cone but the tangent to the Roche lobe at
the inner Lagrangian point. The difference against the osculating cone is too
small to be drawn. Numerically the difference between the model and the
apparent Roche lobe for this small values of the mass ratio is less than 0.2
per cent of the radius for the smaller component and less than 0.5 per cent
of the radius for the larger one. Calculating the light changes of this
configuration, one finds the following (see Fig. 3). There is a large variation
in brightness outside the eclipse but this variation is much lower when the
eclipse begins. This is due to the fact that just at the onset of the
eclipse the osculating cone is projected directly on the surface of the
eclipsed star and the apparent area of this star - not influenced by
eclipse - is now indeed of an ellipsoidal shape. However, in any
rectification process one extrapolates the straight line of fig. 3 which
leads to a variation in brightness that is much larger than really
present. This causes the rectified minima to be much shallower and even
narrower than they really are, leading to orbital elements you hardly
can trust in. Rectifying according to the postulation that the
brightness of the system not influenced by the eclipses remains constant
leads to the light-curve of Fig. 4. One can see a remarkable difference
in depth and shape of the light curves rectified by a classical method
and by applying the Roche model. However, one should be very cautious
when deriving elements from this light curve. This curve no longer is
due to a spherical model. One can get elements from this curve but these
elements still need corrections.
 Fig. 3. Light changes for the Roche-model with low mass ratio. The straight
line is the extrapolation of the light changes outside the eclipses
Fig. 3. Light changes for the Roche-model with low mass ratio. The straight
line is the extrapolation of the light changes outside the eclipses
 Fig. 4. Rectified light curve of AW UMa according to normal rectification (top)
and by applying the Roche-model (bottom)
There may be a way out of these difficulties. In a previous paper of
the author it was shown that one can get three essentially independent
correlations from the Fourier transform of the total light curve. In the
case of a contact configuration there are three main parameters, namely
the ratio of luminosities, the inclination of the orbit and the mass
ratio, which determines fully the geometrical properties of the system.
Therefore it is to be expected that one can solve the problem by the Fourier
method. However, this possibility is still under numerical examination.
REFERENCES
Binnendijk, L., 1965, Kleine Veroff. Bamberg Nr. 40, p. 36.
Paczynski, B., 1964, Astr. J. 69, p. 124.
Kalish, M. S., 1965, Publ. astr. Soc. Pacific 77, p. 36.
Mauder, H., 1966, Kleine Veroff. Bamberg Nr. 38.
DISCUSSION
Avery: What happens, when the stars do not quite fill the Roche lobes?
Mauder: This is a case much more complicated, for you have two additional
parameters that describe the relative radii of both components beside
the mass ratio. You cannot then solve the problem by the Fourier method
but you are forced to use some other method to solve the light curve.
However, if you use the assumption of a contact configuration you
should check whether the solution fits well with the observed light
curve. If there are differences you should carefully discuss the
possibility of components not filling their respective lobes.
Bakos: How would you treat symmetrical light curves?
Mauder: I would symmetrize the light curve by brute force, for I don't know
a physical process which is so well understood till now that you can
apply it in a universal manner on light curves to produce the
asymmetries observed. I think we should be glad if we succeed to get
reasonable elements for W UMa stars without taking into account the
asymmetries.
Wood: Some of these recent developments in means of rectification are
extremely important and may change substantially some of the data
concerning very close eclipsing systems.
Fig. 4. Rectified light curve of AW UMa according to normal rectification (top)
and by applying the Roche-model (bottom)
There may be a way out of these difficulties. In a previous paper of
the author it was shown that one can get three essentially independent
correlations from the Fourier transform of the total light curve. In the
case of a contact configuration there are three main parameters, namely
the ratio of luminosities, the inclination of the orbit and the mass
ratio, which determines fully the geometrical properties of the system.
Therefore it is to be expected that one can solve the problem by the Fourier
method. However, this possibility is still under numerical examination.
REFERENCES
Binnendijk, L., 1965, Kleine Veroff. Bamberg Nr. 40, p. 36.
Paczynski, B., 1964, Astr. J. 69, p. 124.
Kalish, M. S., 1965, Publ. astr. Soc. Pacific 77, p. 36.
Mauder, H., 1966, Kleine Veroff. Bamberg Nr. 38.
DISCUSSION
Avery: What happens, when the stars do not quite fill the Roche lobes?
Mauder: This is a case much more complicated, for you have two additional
parameters that describe the relative radii of both components beside
the mass ratio. You cannot then solve the problem by the Fourier method
but you are forced to use some other method to solve the light curve.
However, if you use the assumption of a contact configuration you
should check whether the solution fits well with the observed light
curve. If there are differences you should carefully discuss the
possibility of components not filling their respective lobes.
Bakos: How would you treat symmetrical light curves?
Mauder: I would symmetrize the light curve by brute force, for I don't know
a physical process which is so well understood till now that you can
apply it in a universal manner on light curves to produce the
asymmetries observed. I think we should be glad if we succeed to get
reasonable elements for W UMa stars without taking into account the
asymmetries.
Wood: Some of these recent developments in means of rectification are
extremely important and may change substantially some of the data
concerning very close eclipsing systems.