Non-Periodic Phenomena in Variable Stars
IAU Colloquium, Budapest, 1968
SUDDEN CHANGES IN THE PERIOD OF ALGOL
T. HERCZEG
Hamburg - Bergedorf
(Read by W. Seitter)
Orbital motion in binary systems was considered, for a long time, a true
paradigm of periodic phenomena. Even its occasional changes were
supposed to be of strictly regular, i.e. periodic nature like rotation
of the apsidal line or light time effects in multiple systems.
Exceptional objects like beta Lyrae, with a secular increase of the period,
could have been recognized as cases still showing some regular,
predictable character. Later on, however, after longer series of
observations became available, a sort of eclipsing systems (like XZ And)
were found showing obviously non-periodic changes of the period: an
erratic but continuous up and down in the O-C diagrams for the times of
minima. Other well observed photometric binaries exhibited a different
type of non-periodic changes: the eclipsing period was, from time to
time, subject to sharp sudden changes ("jumps") while between two
consecutive jumps it remained practically constant. AR Lacertae or AH
Virginis are important examples of this type.
Schneller (1962) in a lecture at the Budapest Observatory advocated his
thesis that, while "regular" changes of the eclipsing period are
relatively infrequent, these sudden, erratic changes seem to be the
rule, at least in the case of the contact and semi-detached systems.
Among other typical objects he mentioned Algol (beta Persei) itself
- certainly one of the best observed variables - as indicating period
changes of this nature; a similar proposal concerning Algol's period, as
a matter of fact, was already put forward by Sterne.
In the case of Algol, Schneller tried to represent the O-C curve of the
times of minima by a polygon having two angles, two "sharp bends". They
correspond to sudden changes, discontinuities of the period, having
occurred in 1840 and 1924. This proposal has been essentially
substantiated by a recent analysis of all photoelectrically determined
epochs of minima, carried out at the Hamburg observatory (cf. a forthcoming
paper by Frieboes-Conde, Herczeg and Hog). In particular, the occurrence of
"period jumps" seems to be definitely established now though numerical details
(like the data of these changes) had to be revised.
This interpretation of the O-C curve offers us an explanation of the
much discussed "great inequality" of Algol, too. This is a hypothetical
long period light time effect requiring the existence of an additional
unseen companion (Algol D) in the system. Up to now there are three observed
and, at least, two hypothetical members listed as belonging to the complicated
Algol system. Those observed, definitely recognized components are:
Algol AB the eclipsing pair, a semi-detached system;
Algol C, a distant companion with a period of 1.862a. This orbital motion
in the triple system gives rise to a light time effect of the times of
minima; having a small amplitude (~~ 6 min.), it is rather difficult to
handle. On the other hand, there exists an accurate and reliable set of
spectroscopic elements for this 1.9 year orbit, derived by Ebbighausen (1958).
The hypothetical members are:
Algol E, introduced for explaining by light time effect a clearly
distinguishable 32-year periodicity of the O-C values by light time effect.
This periodicity can be, however, much more convincingly explained by the aid
of apsidal motion in the eclipsing system;
Algol D, a component proposed already in the last century in order to
find an explication for the above mentioned great inequality, dominant
feature of the O-C diagram, with a suggested period of about 170-180
years. But an interpretation of the great inequality as a light time
effect faces also serious difficulties. Until now, the periodicity
itself defied exact representation: predictions based upon a recent,
very elaborate discussion of the period changes by Kopal, Plavec and
Reilly (1960) yielded residuals amounting to half an hour. Besides, the
mass of this hypothetical unseen companion turns out to be unexpectedly
high, about 4 M_Sun. A further important question is the following: a
possible light time effect would require an orbit large enough to cause
detectable changes (> 1 sec of arc) in the position of Algol AB, a much
observed 2nd magnitude star.
Our discussion of all meridian observation reaching back to about A. D.
1750 indicated, however, that Algol's proper motion remained sensibly
constant - no traces of the orbital motion in the hypothetical quadruple
system Algol ABC-D could be found. This seems to be a direct and decisive
argument against the existence of the component Algol D.
We are now obliged to find an alternative explanation for the great
inequality. Let us make the basic assumption that - besides the eclipsing
period, the 1.9-year light time effect and the 32-year period - no further
periodicities exist in the O-C diagram. (This assumption, which might be
opposed by some observers, has turned out a very useful and also successful
working hypothesis.) Then a rather sensitive test can be carried out, based on
the best determined, photoelectrically observed epochs of minima, about 60
in number since 1920. We treated this rather accurate observational material
in the following way:
We subtracted the effect of 32-years periodicity. This correction was
based on data by Hellerich (1919);
We accepted as a definite representation of the 1.862a orbit the spectroscopic
elements given by Ebbighausen (1958, 1962). Thereafter, the corresponding light
time effect can easily be taken into consideration.
Then the residuals have shown with considerable accuracy a polygon indicating
two sudden changes of the period (in 1944 and 1952) and three different values
of a practically constant eclipsing period outside these "jumps" (Fig. 1).
The sudden changes amount to Delta P = +3.5s and Delta P = -2.0s, respectively.
The constancy of the period within the time intervals, say 1920-1942 and
1955-1965 can be judged from the good representation of the 1.9-year light
time effect, the remaining scatter of the O-C values being but slightly higher
than the usual error of photoelectrically determined epochs of minima. It seems
very improbable that any further periodicities could be accomodated within
this small margin.
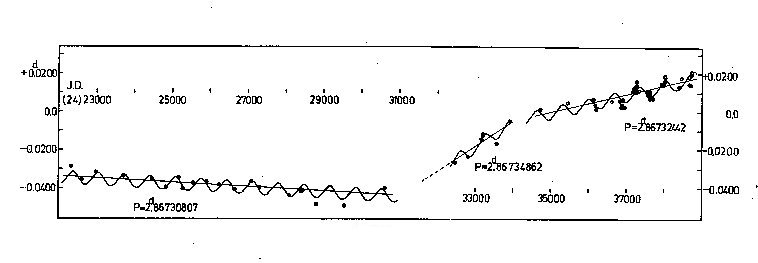 Fig. 1
The reliability of Hellerich's numerical representation of the 22-year
period is, of course, a basic question. Though small systematic deviations are
not to be entirely excluded, no serious error can, - in my opinion - arise
hereby. Especially the fact that the two jumps are rather close together,
separated by a quarter of the period only, means that the existence of
two sudden changes remains incontestable.
This somewhat perhaps surprising representation of the photoelectric
times of minima encourages me to an experiment: to apply a similar
procedure to the earlier measurements, too. Minima were observed since
1784 in a very great number. The overwhelming majority of these times of
minima is based on visual estimates, and their rather modest accuracy
(of the order of +-0.02d), doesn't permit a detection of the 1.9-year
light time effect. Besides, the in fluence of minor systematic errors in
the representation of the 32-year period will be considerably enhanced
by going back to the 18th century observations. This makes our proposed
representation to a tentative one; on the other hand the deviations from
a reasonable picture turn out relatively small, thus suggesting the
proposal I am going to discuss is not completely arbitrary.
Because of the large scatter of the individual epochs I used the normal
points meticulously derived by Ferrari (1934). Again, I subtracted Hellerich's
formula for the 32-year term. The residuals not only allow, they clearly
suggest a representation given by a polygon. The representation derived earlier
from the photoelectric minima is a continuation of this new polygon - the long
interval of constant period 1920-1944 can well be extended back to 1915.
There is no indication of a sudden period change in 1924 as it was proposed
by Schneller; the short sharp change around 1914/15 seems to be real (Fig. 2).
The following table summarizes this possible sequence of "events":
P_1 = 2.8673442d (1784)- 1835 (approx.) Delta P ~~-3.7s
P_2 = 2.8673012d 1835 - 1854 ~~-2.3s
P_3 = 2.8672775d 1854 - 1901 ~~+1.7s
P_4 = 2.8672967d 1901 - 1913 ~~-4.0s
P_5 = 2.8672506d 1913 - 1915 ~~+5.0s
P_6 = 2.86730807d 1915 - 1944 ~~+3.5s
P_7 = 2.86734862d 1944 - 1952 ~~-2.0s
P_8 = 2.86732442d 1952 -(1965)
Fig. 1
The reliability of Hellerich's numerical representation of the 22-year
period is, of course, a basic question. Though small systematic deviations are
not to be entirely excluded, no serious error can, - in my opinion - arise
hereby. Especially the fact that the two jumps are rather close together,
separated by a quarter of the period only, means that the existence of
two sudden changes remains incontestable.
This somewhat perhaps surprising representation of the photoelectric
times of minima encourages me to an experiment: to apply a similar
procedure to the earlier measurements, too. Minima were observed since
1784 in a very great number. The overwhelming majority of these times of
minima is based on visual estimates, and their rather modest accuracy
(of the order of +-0.02d), doesn't permit a detection of the 1.9-year
light time effect. Besides, the in fluence of minor systematic errors in
the representation of the 32-year period will be considerably enhanced
by going back to the 18th century observations. This makes our proposed
representation to a tentative one; on the other hand the deviations from
a reasonable picture turn out relatively small, thus suggesting the
proposal I am going to discuss is not completely arbitrary.
Because of the large scatter of the individual epochs I used the normal
points meticulously derived by Ferrari (1934). Again, I subtracted Hellerich's
formula for the 32-year term. The residuals not only allow, they clearly
suggest a representation given by a polygon. The representation derived earlier
from the photoelectric minima is a continuation of this new polygon - the long
interval of constant period 1920-1944 can well be extended back to 1915.
There is no indication of a sudden period change in 1924 as it was proposed
by Schneller; the short sharp change around 1914/15 seems to be real (Fig. 2).
The following table summarizes this possible sequence of "events":
P_1 = 2.8673442d (1784)- 1835 (approx.) Delta P ~~-3.7s
P_2 = 2.8673012d 1835 - 1854 ~~-2.3s
P_3 = 2.8672775d 1854 - 1901 ~~+1.7s
P_4 = 2.8672967d 1901 - 1913 ~~-4.0s
P_5 = 2.8672506d 1913 - 1915 ~~+5.0s
P_6 = 2.86730807d 1915 - 1944 ~~+3.5s
P_7 = 2.86734862d 1944 - 1952 ~~-2.0s
P_8 = 2.86732442d 1952 -(1965)
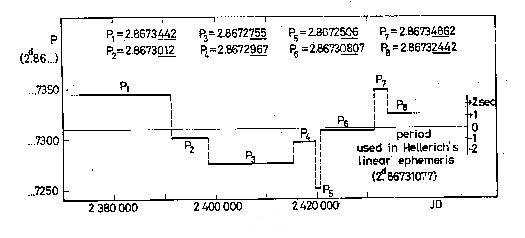 Fig. 2
This interpretation decomposes the great inequality into a series of
sudden period changes. Apparently they are forming a random set, the
changes occurring on an average once in 25-30 years. This is certainly a
non-periodic phenomenon, probably caused by discontinuities of the mass
exchange between the components or in the mass loss from the whole
system. Perhaps, the "overflowing" of the secondary component of its
Roche-limit is not a smooth phenomenon but it causes from time to time
directional outbursts of mass from the secondary, hereby changing the
eclipsing period in a sudden way.
The obviously spurious periodicity of about 160-180 years length was an
understandable suggestion of the early observers: it was favoured by the
existence of two relatively long intervals of constant period. P_1 and P_3.
This led to the use of a mean period in the linear ephemeris formula
which, in its turn, gave rise to the characteristic wedge-shaped figure
in the O-C diagram, simulating the "first half" of a sine curve (Fig. 3).
Fig. 2
This interpretation decomposes the great inequality into a series of
sudden period changes. Apparently they are forming a random set, the
changes occurring on an average once in 25-30 years. This is certainly a
non-periodic phenomenon, probably caused by discontinuities of the mass
exchange between the components or in the mass loss from the whole
system. Perhaps, the "overflowing" of the secondary component of its
Roche-limit is not a smooth phenomenon but it causes from time to time
directional outbursts of mass from the secondary, hereby changing the
eclipsing period in a sudden way.
The obviously spurious periodicity of about 160-180 years length was an
understandable suggestion of the early observers: it was favoured by the
existence of two relatively long intervals of constant period. P_1 and P_3.
This led to the use of a mean period in the linear ephemeris formula
which, in its turn, gave rise to the characteristic wedge-shaped figure
in the O-C diagram, simulating the "first half" of a sine curve (Fig. 3).
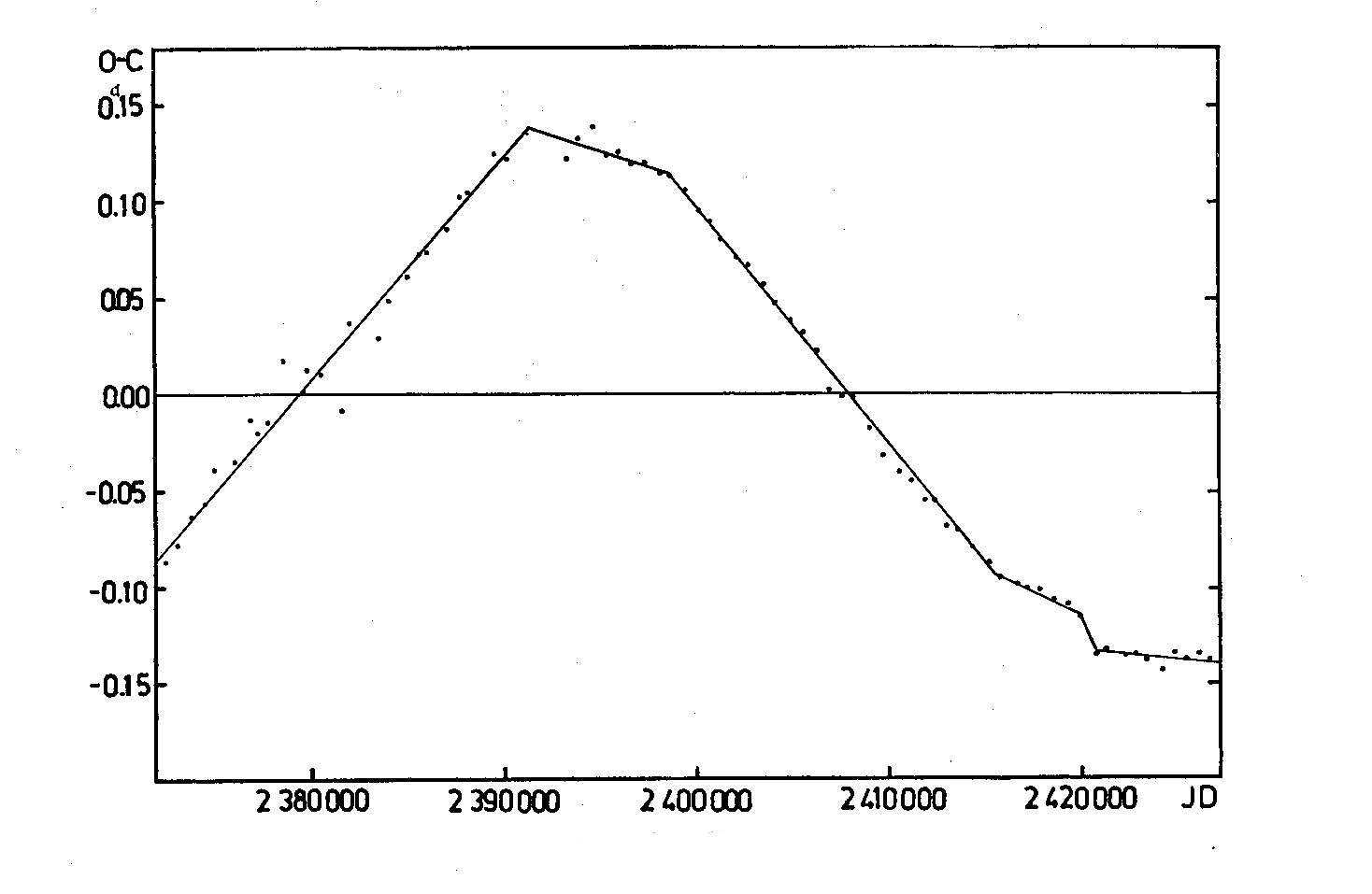 Fig. 3
DISCUSSION
Detre: Algol's O-C diagram looks rather like to one resulting from
cumulative effects of random period variations: on long cycles there are
superposed shorter cycles. How far is the 32 year period established?
Seitter: Irrespective of smaller errors having an effect on the period
length and the zero phase (and Hellerich's representation of the 32 year
period seems to be a very reliable one!), most of the jumps, especially
those rather thoroughly observed in 1944 and 1952, are quite well
established. This is mainly based on the fact that these two jumps
occurred within a time interval short enough not to be seriously
affected by any erroneous assumption concerning the 32 year periodicity.
Numerical data could certainly be shifted to some extent but the
existence of sudden period changes remains beyond doubt.
REFERENCES
Ebbighausen, E. G., 1958, Astrophys. J. 128, 598.
Ebbighausen, E. G., and Gange, J. J., 1962. Publ. Dominion Astrophys.
Obs. Victoria 12, 151.
Ferrari, K., 1934, Astr. Nachr. 253, 225.
Hellerich, J., 1919, Astr. Nachr. 209, 227.
Kopal, Z., Plavec, M. and Reilly, Edith, 1960, Jodrell Bank Ann. 1, 374.
Schneller, H., 1962, Mitt. Sternwarte Budapest No. 53.(CoKon N°.53)
Fig. 3
DISCUSSION
Detre: Algol's O-C diagram looks rather like to one resulting from
cumulative effects of random period variations: on long cycles there are
superposed shorter cycles. How far is the 32 year period established?
Seitter: Irrespective of smaller errors having an effect on the period
length and the zero phase (and Hellerich's representation of the 32 year
period seems to be a very reliable one!), most of the jumps, especially
those rather thoroughly observed in 1944 and 1952, are quite well
established. This is mainly based on the fact that these two jumps
occurred within a time interval short enough not to be seriously
affected by any erroneous assumption concerning the 32 year periodicity.
Numerical data could certainly be shifted to some extent but the
existence of sudden period changes remains beyond doubt.
REFERENCES
Ebbighausen, E. G., 1958, Astrophys. J. 128, 598.
Ebbighausen, E. G., and Gange, J. J., 1962. Publ. Dominion Astrophys.
Obs. Victoria 12, 151.
Ferrari, K., 1934, Astr. Nachr. 253, 225.
Hellerich, J., 1919, Astr. Nachr. 209, 227.
Kopal, Z., Plavec, M. and Reilly, Edith, 1960, Jodrell Bank Ann. 1, 374.
Schneller, H., 1962, Mitt. Sternwarte Budapest No. 53.(CoKon N°.53)
 Fig. 1
The reliability of Hellerich's numerical representation of the 22-year
period is, of course, a basic question. Though small systematic deviations are
not to be entirely excluded, no serious error can, - in my opinion - arise
hereby. Especially the fact that the two jumps are rather close together,
separated by a quarter of the period only, means that the existence of
two sudden changes remains incontestable.
This somewhat perhaps surprising representation of the photoelectric
times of minima encourages me to an experiment: to apply a similar
procedure to the earlier measurements, too. Minima were observed since
1784 in a very great number. The overwhelming majority of these times of
minima is based on visual estimates, and their rather modest accuracy
(of the order of +-0.02d), doesn't permit a detection of the 1.9-year
light time effect. Besides, the in fluence of minor systematic errors in
the representation of the 32-year period will be considerably enhanced
by going back to the 18th century observations. This makes our proposed
representation to a tentative one; on the other hand the deviations from
a reasonable picture turn out relatively small, thus suggesting the
proposal I am going to discuss is not completely arbitrary.
Because of the large scatter of the individual epochs I used the normal
points meticulously derived by Ferrari (1934). Again, I subtracted Hellerich's
formula for the 32-year term. The residuals not only allow, they clearly
suggest a representation given by a polygon. The representation derived earlier
from the photoelectric minima is a continuation of this new polygon - the long
interval of constant period 1920-1944 can well be extended back to 1915.
There is no indication of a sudden period change in 1924 as it was proposed
by Schneller; the short sharp change around 1914/15 seems to be real (Fig. 2).
The following table summarizes this possible sequence of "events":
P_1 = 2.8673442d (1784)- 1835 (approx.) Delta P ~~-3.7s
P_2 = 2.8673012d 1835 - 1854 ~~-2.3s
P_3 = 2.8672775d 1854 - 1901 ~~+1.7s
P_4 = 2.8672967d 1901 - 1913 ~~-4.0s
P_5 = 2.8672506d 1913 - 1915 ~~+5.0s
P_6 = 2.86730807d 1915 - 1944 ~~+3.5s
P_7 = 2.86734862d 1944 - 1952 ~~-2.0s
P_8 = 2.86732442d 1952 -(1965)
Fig. 1
The reliability of Hellerich's numerical representation of the 22-year
period is, of course, a basic question. Though small systematic deviations are
not to be entirely excluded, no serious error can, - in my opinion - arise
hereby. Especially the fact that the two jumps are rather close together,
separated by a quarter of the period only, means that the existence of
two sudden changes remains incontestable.
This somewhat perhaps surprising representation of the photoelectric
times of minima encourages me to an experiment: to apply a similar
procedure to the earlier measurements, too. Minima were observed since
1784 in a very great number. The overwhelming majority of these times of
minima is based on visual estimates, and their rather modest accuracy
(of the order of +-0.02d), doesn't permit a detection of the 1.9-year
light time effect. Besides, the in fluence of minor systematic errors in
the representation of the 32-year period will be considerably enhanced
by going back to the 18th century observations. This makes our proposed
representation to a tentative one; on the other hand the deviations from
a reasonable picture turn out relatively small, thus suggesting the
proposal I am going to discuss is not completely arbitrary.
Because of the large scatter of the individual epochs I used the normal
points meticulously derived by Ferrari (1934). Again, I subtracted Hellerich's
formula for the 32-year term. The residuals not only allow, they clearly
suggest a representation given by a polygon. The representation derived earlier
from the photoelectric minima is a continuation of this new polygon - the long
interval of constant period 1920-1944 can well be extended back to 1915.
There is no indication of a sudden period change in 1924 as it was proposed
by Schneller; the short sharp change around 1914/15 seems to be real (Fig. 2).
The following table summarizes this possible sequence of "events":
P_1 = 2.8673442d (1784)- 1835 (approx.) Delta P ~~-3.7s
P_2 = 2.8673012d 1835 - 1854 ~~-2.3s
P_3 = 2.8672775d 1854 - 1901 ~~+1.7s
P_4 = 2.8672967d 1901 - 1913 ~~-4.0s
P_5 = 2.8672506d 1913 - 1915 ~~+5.0s
P_6 = 2.86730807d 1915 - 1944 ~~+3.5s
P_7 = 2.86734862d 1944 - 1952 ~~-2.0s
P_8 = 2.86732442d 1952 -(1965)
 Fig. 2
This interpretation decomposes the great inequality into a series of
sudden period changes. Apparently they are forming a random set, the
changes occurring on an average once in 25-30 years. This is certainly a
non-periodic phenomenon, probably caused by discontinuities of the mass
exchange between the components or in the mass loss from the whole
system. Perhaps, the "overflowing" of the secondary component of its
Roche-limit is not a smooth phenomenon but it causes from time to time
directional outbursts of mass from the secondary, hereby changing the
eclipsing period in a sudden way.
The obviously spurious periodicity of about 160-180 years length was an
understandable suggestion of the early observers: it was favoured by the
existence of two relatively long intervals of constant period. P_1 and P_3.
This led to the use of a mean period in the linear ephemeris formula
which, in its turn, gave rise to the characteristic wedge-shaped figure
in the O-C diagram, simulating the "first half" of a sine curve (Fig. 3).
Fig. 2
This interpretation decomposes the great inequality into a series of
sudden period changes. Apparently they are forming a random set, the
changes occurring on an average once in 25-30 years. This is certainly a
non-periodic phenomenon, probably caused by discontinuities of the mass
exchange between the components or in the mass loss from the whole
system. Perhaps, the "overflowing" of the secondary component of its
Roche-limit is not a smooth phenomenon but it causes from time to time
directional outbursts of mass from the secondary, hereby changing the
eclipsing period in a sudden way.
The obviously spurious periodicity of about 160-180 years length was an
understandable suggestion of the early observers: it was favoured by the
existence of two relatively long intervals of constant period. P_1 and P_3.
This led to the use of a mean period in the linear ephemeris formula
which, in its turn, gave rise to the characteristic wedge-shaped figure
in the O-C diagram, simulating the "first half" of a sine curve (Fig. 3).
 Fig. 3
DISCUSSION
Detre: Algol's O-C diagram looks rather like to one resulting from
cumulative effects of random period variations: on long cycles there are
superposed shorter cycles. How far is the 32 year period established?
Seitter: Irrespective of smaller errors having an effect on the period
length and the zero phase (and Hellerich's representation of the 32 year
period seems to be a very reliable one!), most of the jumps, especially
those rather thoroughly observed in 1944 and 1952, are quite well
established. This is mainly based on the fact that these two jumps
occurred within a time interval short enough not to be seriously
affected by any erroneous assumption concerning the 32 year periodicity.
Numerical data could certainly be shifted to some extent but the
existence of sudden period changes remains beyond doubt.
REFERENCES
Ebbighausen, E. G., 1958, Astrophys. J. 128, 598.
Ebbighausen, E. G., and Gange, J. J., 1962. Publ. Dominion Astrophys.
Obs. Victoria 12, 151.
Ferrari, K., 1934, Astr. Nachr. 253, 225.
Hellerich, J., 1919, Astr. Nachr. 209, 227.
Kopal, Z., Plavec, M. and Reilly, Edith, 1960, Jodrell Bank Ann. 1, 374.
Schneller, H., 1962, Mitt. Sternwarte Budapest No. 53.(CoKon N°.53)
Fig. 3
DISCUSSION
Detre: Algol's O-C diagram looks rather like to one resulting from
cumulative effects of random period variations: on long cycles there are
superposed shorter cycles. How far is the 32 year period established?
Seitter: Irrespective of smaller errors having an effect on the period
length and the zero phase (and Hellerich's representation of the 32 year
period seems to be a very reliable one!), most of the jumps, especially
those rather thoroughly observed in 1944 and 1952, are quite well
established. This is mainly based on the fact that these two jumps
occurred within a time interval short enough not to be seriously
affected by any erroneous assumption concerning the 32 year periodicity.
Numerical data could certainly be shifted to some extent but the
existence of sudden period changes remains beyond doubt.
REFERENCES
Ebbighausen, E. G., 1958, Astrophys. J. 128, 598.
Ebbighausen, E. G., and Gange, J. J., 1962. Publ. Dominion Astrophys.
Obs. Victoria 12, 151.
Ferrari, K., 1934, Astr. Nachr. 253, 225.
Hellerich, J., 1919, Astr. Nachr. 209, 227.
Kopal, Z., Plavec, M. and Reilly, Edith, 1960, Jodrell Bank Ann. 1, 374.
Schneller, H., 1962, Mitt. Sternwarte Budapest No. 53.(CoKon N°.53)