COMMUNICATIONS MITTEILUNGEN
FROM THE DER
KONKOLY OBSERVATORY STERNWARTE
OF THE DER UNGARISCHEN AKADEMIE
HUNGARIAN ACADEMY OF SCIENCES DER WISSENSCHAFTEN
BUDAPEST - SZABADSAGHEGY
No. 96.
(Vol. 11, Part 3)
NORTHERN CEPHEIDS:
PERIOD UPDATE AND DUPLICITY EFFECTS
L. SZABADOS
BUDAPEST, 1991
ISBN 963 8361 34 4
HU ISSN 0238 - 2091
NORTHERN CEPHEIDS:
PERIOD UPDATE AND DUPLICITY EFFECTS
ABSTRACT
O-C diagrams have been continued for 64 northern Cepheids with the
primary aim of studying the effects of duplicity on the pulsation
period. Because the light-time effect in the O-C diagrams of binary
Cepheids has to be accompanied with properly phased variations in the
gamma-velocity, the radial velocity of the programme stars has been
studied, as well. Light-time effect is suspected in the O-C diagram
of FM Aql, RW Cam, Y Lac, and RS Ori, and confirmed for AW Per. One or
more phase jumps are present or suspected in the O-C diagram of 19
northern Cepheids (FF Aql, BY Cas, DD Cas, DL Cas, X Cyg, SU Cyg, SZ
Cyg, DT Cyg, V532 Cyg, V924 Cyg, TX Del, DX Cem, X Lac, CV Mon, RS Ori,
SV Per, SZ Tau, T Vul, X Vul). In addition to the Cepheids with known
spectroscopic orbit, the spectroscopic binary nature based on the
variability of the gamma-velocity has been confirmed, revealed or
suspected for the majority of the programme stars. The most probable
new spectroscopic binary Cepheids are: KL Aql, Eta Aql, SU Cas, V636
Cas, BZ Cyg, MW Cyg, V386 Cyg, W Gem, RZ Gem, AD Gem, RS Ori, SV Per,
SW Tau, T Vul, and U Vul. A preliminary value of the orbital period is
suggested for Eta Aql, SU Cas, RZ Gem, T Vul, and U Vul.
INTRODUCTION
Period changes of more than a hundred northern Cepheids were studied in
a series of papers (Szabados, 1977, 1980 and 1981, hereinafter referred to
as Papers I, II and III, respectively). As a result, the observed period
changes were compared with the theoretical ones, predicted by the stellar
evolutionary calculations (Szabados, 1983). In addition to the evolutionary
changes (manifested in parabolic O-C graphs), two special kinds of period
variations were also revealed in several cases, both of them being
characteristic of binary Cepheids:
1. light-time effect due to the orbital motion,
2. phase jump, i.e. a stepwise O-C graph.
The origin of this latter type of the period change has not been clarified
yet, but the phase jumps always occur in Cepheids having a companion star.
Later on, it became obvious that the extension of that study to
southern Cepheids was of importance because the period variation of most
Cepheids with negative declination had not been followed closely. The
investigation of 44 bright southern Cepheid variables was published
recently (Szabados, 1989 = Paper IV). Because the programme stars were
selected arbitrarily, the primary goal of Paper IV was the study of
duplicity effects in the O-C diagram, and no special attention was
paid to follow the evolutionary period changes.
A companion star can also alter the observable gamma-velocity of the given
variable, if the orbital inclination significantly differs from zero. A
light-time effect in the O-C diagram has to be accompanied with properly
phased gamma-velocity variations of the same period, and the amplitude of the
oscillation in the O-C diagram is not independent from that deduced from
the diagram gamma-velocity vs. time. For this reason the study of period
changes was supplemented with a comprehensive study of gamma-velocity
variations of the programme stars.
By the end of the eighties it became obvious that the frequency of the
Cepheid binaries is much higher than thought before (Szabados, 1990b). The
increase of the known spectroscopic binaries among Cepheids is mostly a
result of the ultraviolet spectroscopy made with the IUE-satellite, and the
thorough radial velocity studies performed in the last decade. In some
cases, however, the available, sometimes sporadic, radial velocity
measurements were even sufficient for revealing the orbital effect, or
determining the orbital period (see e.g. Szabados, 1990a).
The aim of the present paper is to analyse the period changes of the
known binary Cepheids of the northern sky, in order to study the effects of
duplicity, and to search for gamma-velocity variations in the case of
suspected binary Cepheids with a declination larger than zero. Therefore
the sample of stars studied here is selected arbitrarily: it contains 64
stars of various brightness (including four Population II Cepheids). Even
some of the brightest Cepheids have been omitted (e.g. delta Cephei itself),
being very probably single stars. Their period changes have to be also
studied, but this paper is the last one in the extensive series on this
topic, and the similar studies in the future will concentrate on individual
Cepheids. Unfortunately the variable star astronomers have lost their
interest in the regular photometry of the Cepheid variables, and it is to
be afraid that the subtle but important period changes in these stars will
pass unnoticed.
The programme stars are arranged in alphabetical order of
constellations. The list of the Cepheids involved in this study is as
follows (the ordinal number following the name of the Cepheid gives the
page number where the discussion on the given star begins):
Cepheid page Cepheid page Cepheid page
SZ Aql 129 SZ Cyg 161 BG Lac 197
TT Aql 131 TX Cyg 163 T Mon 198
FF Aql 132 VZ Cyg 164 SV Mon 200
FM Aql 134 BZ Cyg 166 CV Mon 202
KL Aql 135 DT Cyg 167 V465 Mon 203
V572 Aql 136 MW Cyg 169 RS Ori 204
V1344 Aql 137 V386 Cyg 170 GQ Ori 206
Eta Aql 138 V532 Cyg 172 SV Per 206
RT Aur 140 V924 Cyg 174 VX Per 208
AN Aur 142 V1334 Cyg 175 AS Per 209
RW Cam 143 V1726 Cyg 177 AW Per 210
SU Cas 145 TX Del 177 V440 Per 212
SZ Cas 147 W Gem 178 S Sge 213
RY Cas 148 RZ Gem 180 SW Tau 216
DD Cas 150 AD Gem 182 SZ Tau 217
DL Cas 151 DX Gem 183 S Vul 219
IX Cas 153 zeta Gem 185 T Vul 220
V636 Cas 154 V Lac 189 U Vul 223
IR Cep 155 X Lac 191 X Vul 224
V351 Cep 156 Y Lac 193 SV Vul 226
X Cyg 157 Z Lac 194
SU Cyg 159 RR Lac 196
In addition to the binary Cepheids, some other Cepheid variables not
having a companion were also studied, provided that the construction of a
new O-C diagram contains relevant new information as compared with the
original O-C plot published in Papers I-III. The new piece of information
can be a recent period change, or larger accuracy due the new photoelectric
O-C residuals overwhelming in the present O-C diagrams. Similarly, the
shape of the O-C diagram is differently interpreted in the case of several
binary Cepheids, as compared with the previous one. Besides the reasons
listed above, the main cause of the modified shape of the O-C graphs is a
recently discovered phase jump.
Since the duplicity effects in the O-C diagram (light-time effect and
phase jump) are usually very subtle, only the photoelectric observations
have been taken into account whenever possible. In a number of cases,
however, photographic observations were also used when constructing the
new O-C diagram, and for seven Cepheids (SU Cyg, VZ Cyg, W Gem, RZ Gem,
zeta Gem, X Lac, SV Per) the early visual observations were also analysed.
These latter exceptional cases are examples for either a parabolic O-C
graph or an early phase jump, therefore the visual observations even from
the last century are of primary importance.
The O-C residuals taken from Papers I-III have the same weight as that
assigned to them originally. As far as the visual and the photographic
observations are concerned, the O-C residuals based on such observations
with a weight less than unity have not been used here.
The recently published photoelectric light curves are often superior to
the previous ones. The new normal light curve determined for more than
twenty programme stars showed a marked difference as compared with the
previously used normal curve. In these cases the O-C residuals taken from
Papers I-III were corrected accordingly. It has to be noted that, although
solely photoelectric data have been used from among the recently published
observations, several photoelectric observational series have been omitted,
i.e. those obtained in the IR-region (e.g. Schmidt, 1976; Welch et al.,
1984) because of the uncertain phase shift between the moments of maxima in
the blue and infrared bands.
In the following discussion there are usually two tables and one figure
for each Cepheid. The successive columns of the tables containing
information on the O-C residuals give the following data:
1. Moment of normal maximum (an asterisk indicates that the given moment is
a new one, not appearing in Papers I-III),
2. The corresponding epoch,
3. O-C residual (in days),
4. The weight assigned to the residual (a blank character means that the
given residual has not been used in the curve-fitting procedure),
5. Source of the observational data.
The epoch and the O-C residual have been obtained using the linear
ephemeris given in the discussion on each Cepheid.
The determination of the gamma-velocities was performed in a similar
manner as described in Paper IV. The successive columns in the Tables of
the gamma-velocities contain the following data:
1.-2. Mean date of the observations and its formal standard deviation,
3.-4. gamma-velocity and its formal standard deviation,
5. Number of radial velocity observations used,
6. Source of the observational data.
Note that the uncertainty in the zero-point of the individual radial
velocity measurement series tends to increase the standard deviation given
in the tables, but no allowance was made for the zero-point differences.
The gamma-velocity of a programme star is considered to be variable if its
variation is larger than five km/s. The uncertainty of the zero-point
hardly exceeds one km/s in the case of the modern radial velocity
observations. The gamma-velocity of the Cepheid-binaries with known orbit is
not analysed here.
The figures visualizing the tabular data are usually divided into two
parts. The upper panel shows the O-C diagram of the given variable. Filled
circles denote the O-C residuals based on photoelectric observations, while
open circles are those of photographic (or visual, in the case of the seven
Cepheids listed above) origin. The size of the circles refers to the weight
assigned to the O-C residual. The least squares fit (usually linear or
parabolic) is also shown. It has to be noted, however, that the O-C
residuals earlier than J.D. 2420000 are not plotted, even if they are
listed in the corresponding table because those particular residuals
were used during the curve-fitting procedure. In several cases sections of
the O-C graph not studied here are also drawn for convenience (without
listing the corresponding visual or low quality photographic O-C
residuals). The ephemeris used for obtaining the O-C residuals is indicated
at the top of the figure.
The lower panel of the figures shows the individual gamma-velocities as a
function of the Julian Date. The reliability of the data points can be
estimated from the error bars (if the standard deviation exceeds the size
of the dot). Again, the figure does not show the tabular values before J.D.
2420000.
REMARKS ON THE INDIVIDUAL VARIABLES
SZ Aquilae
The three more recent photoelectric observational series confirm the
previous conclusion (Paper III) about the continuous period increase. The
new O-C diagram has been constructed using the elements:
C = 2443807.165 + 17.140554d*E (1)
+-.032 +-.000233
The momentary value of the period is as follows:
P = 17.140554d + 3.29d*E*10^-6 (2)
+-.000233 +-.64
Table 1. O-C residuals for SZ Aql
Norm.max. E O-C W Reference
JD2400000+
29513.184 -834 1.487 Ahnert (1951)
29838.681 -815 1.308 Erleksova (1960)
31638.130 -710 0.758 Erleksova (1960)
32460.734 -662 0.616 Erleksova (1960)
33112.198 -624 0.739 3 Eggen (1951)
33454.820 -604 0.550 Erleksova (1960)
34414.613 -548 0.472 Erleksova (1960)
35494.235 -485 0.239 Erleksova (1960)
35580.096 -480 0.397 1 Walraven et al. (1958)
36231.149 -442 0.109 Erleksova (1960)
37156.786 -388 0.156 2 Mitchell et al. (1964)
37945.611 -342 0.515 1 Williams (1966)
40910.526 -169 0.115 3 Pel (1976)
41338.940* -144 0.015 3 Feltz & McNamara (1980)
42898.836 -53 0.120 2 Dean (1977)
43807.095 0 -0.070 3 Szabados (1981)
44441.228* 37 -0.137 2 Eggen (1983b)
44612.842* 47 0.071 3 Moffett & Barnes (1984)
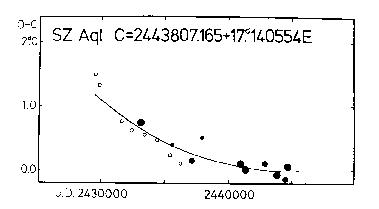
Figure 1. O-C diagram of SZ Aql
The O-C residuals are listed in Table 1 and shown plotted in Figure 1. The
small number of radial velocity data (Joy, 1937; Barnes et al., 1988) does
not allow the determination of accurate gamma-velocities.
TT Aquilae
This bright Cepheid was frequently observed photometrically in the
last two decades, thus making possible the reliable period determination
based on photoelectric observations alone (see Table 2 and Figure 2). The
current ephemeris is as follows:
C = 2443810.958 + 13.754954d*E (3)
+-.014 +-.000043
Although the O-C residuals based on the photographic and the early
photoelectric observations suggest a wave-like pattern, this tendency
disappears after J.D. 2440000, as if a sudden change in the pulsation
period occurred.
It is worth mentioning that the Julian Dates in Connolly et al.'s
(1982) paper need a correction of -1 day. The revised pulsation period in
their paper is also an arjpgact of this mistake.
The gamma-velocities of TT Aql are collected in Table 3, and are shown
plotted in the lower panel of Figure 2. A slight variation in the average
radial velocity cannot be excluded but further high quality observations
Table 2. O-C residuals for TT Aql
Norm.max. E O-C W Reference
JD2400000+
29385.963 -1016 0.038 Erleksova (1960)
30564.956 -963 0.019 Erleksova (1960)
31527.765 -893 -0.019 Erleksova (1960)
32449.337 -826 -0.029 Erleksova (1960)
33109.654 -778 0.050 3 Eggen (1951)
33494.741 -750 -0.002 Erleksova (1960)
34416.368 -683 0.044 Erleksova (1960)
35282.936 -620 0.049 2 Irwin (1961)
35502.954 -604 -0.012 Erleksova (1960)
35558.014 -600 0.028 2 Walraven et al. (1958)
36218.152 -552 -0.071 Erleksova (1960)
37208.525 -480 -0.055 3 Mitchell et al. (1964)
37937.601 -427 0.008 1 Williams (1966)
40413.494* -247 0.010 2 Feltz & McNamara (1980)
40867.193 -214 -0.205 1 Evans (1976)
40867.331 -214 -0.067 3 Pel (1976)
41266.313* -185 0.021 2 Feltz & McNamara (1980)
41912.777 -138 0.003 3 Landis (1976)
42916.670 -65 -0.216 2 Dean (1977)
43343.343* -34 0.053 3 Moffett & Barnes (1984)
43810.884 0 -0.074 3 Szabados (1981)
43865.980* 4 0.002 3 Moffett & Barnes (1984)
44443.719* 46 0.033 3 Connolly et al. (1982)
44443.719* 46 0.033 3 Coulson et al. (1985)
44512.589* 51 0.128 3 Eggen (1983b)
44691.332* 64 0.057 2 Connolly et al. (1982)
44828.824* 74 -0.001 2 Coulson et al. (1985)
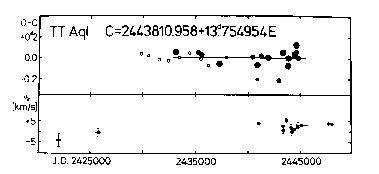
Figure 2. Upper panel: O-C diagram of TT Aql
Lower panel: gamma-velocities for the same Cepheid
Table 3. gamma-velocities of TT Aql
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
22002 152 -4.1 3.2 3 Joy (1937)
25809 260 -0.4 1.8 7 Joy (1937)
41031 146 4.0 0.2 7 Evans & Lyons (1986)
43317 31 3.0 0.4 3 Evans & Lyons (1986)
43369 36 0.8 1.2 12 Wilson et al. (1989)
43688 75 5.5 1.0 16 Barnes et al. (1987)
44036 47 2.1 1.8 6 Barnes et al. (1987)
44180 3 0.1 1.4 4 Coulson et al. (1985)
44427 10 1.3 0.5 27 Coulson et al. (1985)
44778 1 2.2 2.5 2 Coulson et al. (1985)
45133 521 3.3 0.2 7 Evans & Lyons (1986)
47745 34 3.9 0.4 15 Samus (1990)
48044 42 3.8 0.4 18 Samus (1990)
are necessary to make a firm statement. Leonard and Turner (1986)
summarized the available information on duplicity of TT Aql. Although the
photometric test by Madore and Fernie (1980) suggests the presence of a
bright blue companion, no other positive evidence is available (see Evans,
1985; Coulson et al., 1986).
FF Aquilae
This variable is one of the most popular Cepheids among the observers,
therefore a number of new results has been achieved. As to its photometry,
the new O-C diagram (see Figure 3 and Table 4) clearly shows the existence
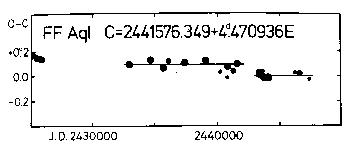
Figure 3. O-C diagram of FF Aql
Table 4. O-C residuals for FF Aql
Norm.max. E O-C W Reference
JD2400000+
25096.650 -3686 0.171 3 Huffer (1931)
25490.067 -3598 0.146 3 Huffer (1931)
25811.968 -3526 0.139 3 Huffer (1931)
32960.946 -1927 0.091 3 Eggen (1951)
34628.641 -1554 0.127 3 Szabados (1977)
35625.598 -1331 0.065 3 Walraven et al. (1958)
36099.567 -1225 0.115 2 Svolopoulos (1960)
37320.127 -952 0.109 3 Mitchell et al. (1964)
39019.100 -572 0.126 3 Wisniewski & Johnson (1968)
40266.395* -293 0.030 1 Feltz & McNamara (1980)
40789.448* -176 -0.016 1 Feltz & McNamara (1980)
40811.901 -171 0.082 3 Pel (1976)
41245.539* -74 0.039 2 Feltz & McNamara (1980)
41576.448 0 0.099 3 Szabados (1977)
43342.376* 395 0.007 3 Moffett & Barnes (1984)
43369.211* 401 0.017 3 present paper
43615.129* 456 0.033 1 Henden (1979)
43673.206* 469 -0.012 3 Moffett & Barnes (1984)
43731.324* 482 -0.016 3 present paper
44035.355* 550 -0.009 2 Moffett & Barnes (1984)
44853.537* 733 -0.008 3 Arellano Ferro (1984)
46284.270* 1053 0.025 1 "Carlsberg" (1989)
46624.056* 1129 0.020 2 present paper
47455.601* 1315 -0.029 1 Usenko (1990a)
of a phase jump, a phenomenon that has already been suspected by Evans et
al. (1990b) on the basis of the new radial velocity data. The O-C residuals
in Table 4 have been computed using the ephemeris:
C = 2441576.349 + 4.470936d*E (4)
+-.009 +-.000014
and this ephemeris is valid for predicting the maxima after J.D. 2443000.
Between J.D. 2433000 and 2442000 the following formula gives the best fit
to the O-C residuals:
C = 2441576.423 + 4.470918d*E (5)
+-.011 +-.000010
Therefore the pulsation period remained constant during the two
sections of the O-C graph, while the amount of the phase shift is about
0.08 day (or 0.02 phase). The phase jump occurred between J.D. 2442000 and
2443000. The different values of the pulsation period as determined from
the O-C diagrams for the maximum and median brightness (see Paper I, page
92) can now be interpreted as a minor change in the light curve shape
similarly to the other known case of SU Cyg (see Paper I and this paper,
p. 159).
The radial velocity measurements of FF Aql are not analysed here
because the study of Evans et al. (1990b) is so thorough and complete.
Their paper includes a new determination of the orbit, and also contains
all the available information concerning the companions to FF Aql. The only
contribution here to the spectroscopic study is a single radial velocity
measurement listed in Table 109.
FM Aquilae
The new O-C diagram based on only photoelectric observations (see
Table 5 and Figure 4) gives a slightly longer period than that determined
in Paper II. The new ephemeris is as follows:
C = 2442678.253 + 6.114265d*E (6)
+-.006 +-.000008
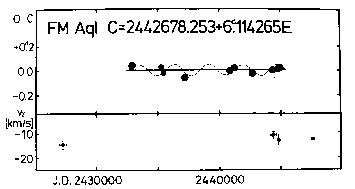
Figure 4. Upper panel: O-C diagram of FM Aql
Lower panel: gamma-velocities for the same Cepheid
Table 5. O-C residuals for FM Aql
Norm.max. E O-C W Reference
JD2400000+
32962.724 -1589 0.038 3 Eggen (1951)
35292.245 -1208 0.024 2 Irwin (1961)
35500.086 -1174 -0.020 2 Walraven et al. (1958)
37187.583 -898 -0.060 3 Mitchell et al. (1964)
40819.509 -304 -0.007 3 Pel (1976)
41223.078* -238 0.020 3 Feltz & McNamara (1980)
42678.229 0 -0.024 3 Szabados (1980)
44335.221* 271 0.002 3 Moffett & Barnes (1984)
44830.486* 352 0.012 3 Eggen (1985)
44983.348* 377 0.017 3 Moffett & Barnes (1984)
Table 6. gamma-velocities of FM Aql
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
27219 278 -14.5 1.7 8 Joy (1937)
44391 192 -10.8 1.4 9 Barnes et al. (1988)
44821 45 -12.8 2.3 4 Barnes et al. (1988)
47648 4 -12.4 0.2 6 Samus (1990)
Moreover, an apparent period variation caused by the light-time effect may
be superimposed on the O-C graph (see Figure 4). The estimated period
(about 2800 days) and the amplitude of the sinusoidal variation implies an
orbital radial velocity variation that might be easily detected.
The available radial velocity measurements (see Table 6), however, do
not support the variable gamma-velocity hypothesis. Nevertheless, there have
been evidence in favour of a blue companion. Madore (1977) derived a B9V
type photometric companion, while Pel (1978) concluded that FM Aql had a
peculiar colour - colour loop. The ultraviolet spectrum of this Cepheid,
however, does not indicate the presence of a companion earlier than A0V
(Evans et al. 1990a). Further spectroscopic observations are desirable to
settle this problem.
KL Aquilae
There are no newly published photometric observations on this
neglected Cepheid, thus the previous O-C diagram (Paper II, p. 53) cannot
be replaced with a recent one. The existing radial velocity measurements,
however, have not been analysed before. As one can see in Table 7, the
gamma-velocities show a strong variation on a time-scale of several hundred
days. KL Aql seems to be a new spectroscopic binary Cepheid, worthy of
immediate observation.
Table 7. gamma-velocities of KL Aql
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
27543 124 -1.5 2.0 6 Joy (1937)
28097 1 -6.8 4.5 1 Joy (1937)
28396 21 -45.5 1.4 3 Abt (1973)
44735 129 -0.5 1.2 12 Harris & Wallerstein (1984)
45167 48 1.0 2.0 5 Harris & Wallerstein (1984)
V572 Aquilae
All the previous photoelectric observations have been analysed again,
because Henden's (1979) data form a better normal light curve than that
used in Paper I. Therefore the moments of the normal maxima listed in
Table 8 are different from the corresponding values listed in Paper I (p.
70). In spite of the reliable new normal light curve, the O-C residuals
widely scatter around the best fitting line (see Figure 5) described with
the formula:
C = 2441921.693 + 3.768001d*E (7)
+-.088 +-.000080
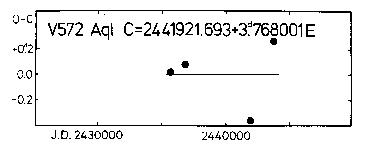
Figure 5. O-C diagram of V572 Aql
Table 8. O-C residuals for V572 Aql
Norm.max. E O-C W Reference
JD2400000+
35666.826 -1660 0.015 3 Walraven et al. (1958)
36789.753 -1362 0.077 3 Oosterhoff (1960)
41921.334 0 -0.359 3 Szabados (1977)
43734.368* 481 0.267 3 Henden (1979)
These deviations are possibly caused by period changes (a previous change
in the pulsation period was suspected in Paper I). Therefore the elements
given here and in Table 110 are only tentative.
No radial velocity measurements have been published about this star.
V1344 Aquilae
Arellano Ferro's (1984) recent photoelectric observations form a new
normal light curve superior to the previous one (Kovacs and Szabados,
1979), therefore these earlier published observations were re-analysed
when constructing the O-C diagram. The O-C residuals plotted in Figure 6
and listed in Table 9 have been calculated with the ephemeris:
C = 2443398.184 + 7.476787d*E (8)
+-.015 +-.000104
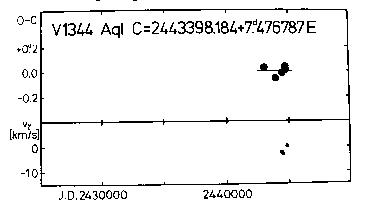
Figure 6. Upper panel: O-C diagram of V1344 Aql
Lower panel: gamma-velocities for the same Cepheid
Table 9. O-C residuals for V1344 Aql
Norm.max. E O-C W Reference
JD2400000+
43016.896 -51 0.028 3 Kovacs & Szabados (1979)
43958.889 75 -0.054 3 Kovacs & Szabados (1979)
44482.301* 145 -0.017 3 Fernie & Garrison (1981)
44781.430* 185 0.040 3 Arellano Ferro (1984)
44788.871* 186 0.005 3 Eggen (1985)
Table 10. gamma-velocities of V1344 Aql
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
44424 27 -2.3 0.1 16 Balona (1981)
44528 15 -2.7 0.2 8 Balona (1981)
44832 6 0.2 0.6 8 Arellano Ferro (1984)
The available radial velocity data, although being very accurate, are
not sufficient to draw a firm conclusion on the variability of the
gamma-velocity (see Table 10). If V1344 Aql is really a spectroscopic
binary, then the orbital period has to be relatively short (several
hundred days). An extension of the observations to a longer time-base
both in photometry and spectroscopy would be necessary.
Eta Aquilae
Because the photoelectric observations obtained by Moffett and Barnes
(1984) offered a better normal ligth curve than that used previously, this
new normal curve has been used for determining the moments of normal
maxima for the photoelectric observations published in the eighties. In
order to eliminate the systematic difference in the phase of the maximum
light between the recent and the previous normal curve, a correction of
-0.029 day has been applied to the photoelectric O-C residuals published
in Paper II. Both the corrected and the recently determined O-C residuals
are listed in Table 11. A parabolic fit, i.e. a continuously increasing
pulsation period is still the most appropriate interpretation of the O-C
graph (see Figure 7). The O-C residuals have been calculated using the
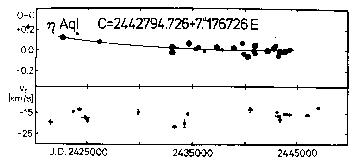
Figure 7. Upper panel: O-C diagram of Eta Aql
Lower panel: gamma-velocities for the same Cepheid
ephemeris:
C = 2442794.726+ 7.176726d*E (9)
+-.006 +-.000014
The instantaneous value of the period can be predicted as follows:
p = 7.176726d+ 3.16d*E*10^-8 (10)
+-.000014 +-1.13
There is no significant difference between this value and that determined
in Paper II.
Table 11. O-C residuals for n Aql
Norm.max. E O-C W Reference
JD2400000+
22585.188 -2816 0.122 3 Wylie (1922)
23991.859 -2620 0.155 1 Pettit & Nicholson (1933)
26144.796 -2320 0.074 2 Bernheimer (1931)
33041.532 -1359 -0.023 3 Eggen (1951)
33070.289 -1355 0.027 3 Stebbins et al. (1952)
34613.324 -1140 0.066 3 Szabados (1980)
35295.055 -1045 0.008 2 Irwin (1961)
35574.965 -1006 0.025 2 Walraven et al. (1958)
36141.892 -927 -0.009 1 Oke (1961)
37283.027 -768 0.027 3 Mitchell et al. (1964)
37857.144 -688 0.005 1 Williams (1966)
38926.492 -539 0.021 3 Wisniewski & Johnson (1968)
39751.864 -424 0.070 2 Sudzius (1969)
39888.119 -405 -0.033 2 Schmidt (1971)
40239.753* -356 -0.058 3 Feltz & McNamara (1980)
40857.010* -270 0.000 2 Feltz & McNamara (1980)
40928.825 -260 0.048 3 Pel (1976)
40957.453 -256 -0.031 2 Evans (1976)
42127.285* -93 -0.005 3 Depenchuk (1980)
42794.752 0 0.026 3 Szabados (1980)
42945.483 21 0.046 2 Dean (1977)
43203.745* 57 -0.054 2 Depenchuk (1980)
43311.439* 72 -0.011 2 Dean (1981)
43340.153* 76 -0.004 3 Moffett & Barnes (1984)
43864.047* 149 -0.011 3 Moffett & Barnes (1984)
44373.617* 220 0.011 2 Schmidt & Parsons (1982)
The study of the radial velocity observations, however, gives more
novelty. It is a well-known fact that Eta Aql belongs to a binary system
(Mariska et al., 1980). Based on the IUE spectra, Bohm-Vitense and Proffitt
(1985) derived an A1V companion of Delta V = 4.6 mag. Jacobsen and
Wallerstein (1981) suspected long period changes in the systemic radial
velocity. As a matter of fact, the analysis of the radial velocity data
collected from the literature (see Table 12 and Figure 7) strengthens
their conclusion on the variability of the gamma-velocity. It is not clear,
however, what period can be assigned to the gamma-velocity changes. The
formal period search resulted in a value as short as 926 days. The
deviations of the O-C residuals from the fitted parabola clearly show a
Table 12. gamma-velocities of Eta Aql
J.D. sigma v gamma sigma n Reference
2400000+[d] [km/s] [km/s]
14129 10 -16.7 0.9 13 Belopolski (1897)
14517 32 -15.0 0.6 28 Wright (1899)
19277 366 -13.7 2.1 3 Spencer Jones (1928)
21429 233 -19.6 1.2 4 Abt (1973)
23653 43 -14.4 0.6 28 Jacobsen (1926)
24226 173 -13.4 0.4 57 Henroteau (1928)
24869 461 -17.6 0.9 6 Abt (1973)
25084 23 -18.9 0.8 17 Henroteau & Vibert (1929)
29873 12 -14.6 1.2 4 Jacobsen (1961)
33292 190 -21.6 0.4 22 Jacobsen (1954)
34258 15 -19.8 2.0 2 Jacobsen (1954)
34548 32 -15.3 0.6 14 Jacobsen (1.961)
40502 139 -13.3 1.0 5 Lloyd Evans (1980)
43049 33 -14.3 0.7 3 Jacobsen & Wallerstein (1981)
43141 206 -16.3 0.3 7 Beavers & Eitter (1986)
43384 4 -17.9 1.3 11 Wilson et al. (1989)
43828 206 -15.2 0.7 29 Barnes et al. (1987)
44290 143 -15.4 0.2 18 Jacobsen & Wallerstein (1981)
46033 157 -16.0 0.2 18 Jacobsen & Wallerstein (1987)
47027 1 -12.5 0.7 1 Samus (1990)
sinusoidal pattern at this period, as if it were a light-time effect, but
this is too subtle to detect with an eye inspection in Figure 7. Further
extensive radial velocity measurements are necessary to find the correct
value of the spectroscopic orbital period.
RT Aurigae
Table 13. O-C residuals for RT Aur
Norm.max. E O-C W Reference
JD2400000+
29603.272 -3251 -0.035 3 Bennett (1941)
33141.392 -2302 0.025 3 Eggen et al. (1957)
35799.601 -1589 0.029 3 Prokof'yeva (1961)
35881.611* -1567 0.018 3 Bahner & Mavridis (1977)
36202.239* -1481 0.021 3 Bahner & Mavridis (1977)
36616.072* -1370 0.024 2 Bahner & Mavridis (1977)
37339.350 -1176 0.032 3 Mitchell et al. (1964)
37995.423 -1000 -0.058 2 Williams (1966)
38920.047 -752 -0.027 3 Wisniewski & Johnson (1968)
39359.960 -634 -0.041 3 Takase (1969)
40843.831* -236 0.007 2 Feltz & McNamara (1980)
40996.642* -195 -0.038 2 Evans (1976)
41429.115 -79 -0.036 3 Winzer (1973)
41723.711 0 0.032 3 Szabados (1977)
43539.286* 487 -0.025 2 Moffett & Barnes (1984)
44106.001* 639 0.003 3 Moffett & Barnes (1984)
44534.795* 754 0.055 2 Eggen (1985)
The eight new O-C residuals supplemented with the earlier photoelectric
O-C values (see Table 13) confirm the value of the pulsation period as
determined in Paper I. The O-C diagram has been calculated using the
formula:
C = 2441723.679 + 3.728198d*E (11)
+-.006 +-.000005
Although a very long (10000 - 15000 days) wave may be superimposed on the
straight line in Figure 8, no spectroscopic confirmation of the light-time
effect can be deduced from the available radial velocity data (Table 14).
Leonard and Turner (1986) summarized the various arguments for and
against duplicity of RT Aur and concluded that this Cepheid probably
does not have a bright blue companion.

Figure 8. Upper panel: O-C diagram of RT Aur
Lower panel: gamma-velocities for the same Cepheid
Table 14. gamma-velocities of RT Aur
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
18230 18 21.5 0.6 24 Petrie (1932)
21210 65 19.5 0.6 30 Kiess (1917)
23723 30 20.6 1.3 6 Petrie (1932)
24955 253 20.1 0.7 19 Petrie (1932)
40979 9 21.0 0.3 4 Evans (1976)
43449 59 20.0 1.4 9 Wilson et al. (1989)
43457 275 18.7 0.4 5 Beavers & Eitter (1986)
43963 245 18.0 0.8 25 Barnes et al. (1987)
45717 9 20.4 0.1 45 Gieren (1985)
46866 1 20.4 0.5 2 Samus (1990)
AN Aurigae
Berdnikov's (1987) recent photometry confirms the period change
suspected in Paper III but the phase jump interpretation does not seem to
be correct. The O-C residuals listed in Table 15 have been obtained by the
formula:
C = 2443799.022 + 10.289563d*E (12)
+-.017 +-.000036
The photoelectric O-C residuals are plotted in Figure 9. It should be noted
that Berdnikov's (1987) photoelectric observations do not support the
change in the light curve shape suspected in Paper III.
Nevertheless, AN Aur is a binary Cepheid, since the radial velocity
observations show a variation in the gamma-velocity. In Figure 10 the open
circles denote Joy's (1937) radial velocity data, while Samus' (1990)
observations are plotted as filled circles. Zero phase is chosen
arbitrarily, the pulsation period is according to Eq.(12). The deviation
in the average radial velocity is even more obvious if the phase shift due
to the period change occurred after the epoch of Joy's observations is
also taken into account. Madore (1977) estimates a B5 photometric
companion. Further spectroscopic observations of this Cepheid would be of
primary importance.
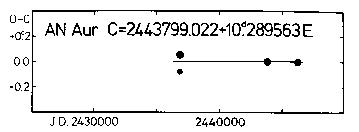
Figure 9. O-C diagram of AN Aur
Table 15. O-C residuals for AN Aur
Norm.max. E O-C W Reference
JD2400000+
36832.907 -677 -0.081 2 Oosterhoff (1960)
36833.041 -677 0.053 3 Weaver et al. (1960)
43799.026 0 0.004 3 Szabados (1981)
46299.383* 243 -0.003 3 Berdnikov (1987)
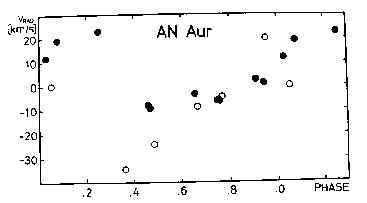
Figure 10. Radial velocity observations of AN Aur folded with the period
10.289563 days. Zero phase is chosen arbitrarily. Open circles:
Joy's (1937) data, filled circles: Samus'(1990) observations
RW Camelopardalis
The O-C diagram of this binary Cepheid supplemented with the recent
O-C residuals (see Table 16) is plotted in Figure 11. The O-C residuals
have been calculated using the ephemeris:
C = 2443840.694 + 16.415015d*E (13)
+-.020 +-.000067
If the wave-like pattern is interpreted in terms of the light-time effect,
an orbital period of about 7000 days characterizes the system. In
Table 16. O-C residuals for RW Cam
Norm.max. E O-C W Reference
JD2400000+
36174.873 -467 -0.009 3 Bahner & Mavridis (1977)
36831.480 -427 -0.003 3 Oosterhoff (1960)
36831.546 -427 0.063 3 Weaver et al. (1960)
36880.608 -424 -0.120 3 Bahner et al. (1962)
39113.340 -288 0.170 3 Wamsteker (1972)
39786.182 -247 -0.003 2 Szabados (1981)
43840.515 0 -0.179 3 Szabados (1981)
44382.394* 33 0.005 2 Moffett & Barnes (1984)
45038.953* 73 -0.037 3 Moffett & Barnes (1984)
45695.611* 113 0.020 3 Berdnikov (1986)
46483.539* 161 0.028 2 present paper
47304.378* 211 0.116 2 present paper
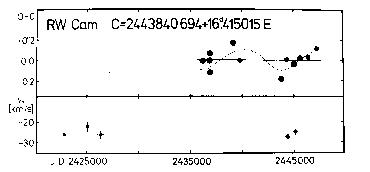
Figure 11. Upper panel: O-C diagram of RW Cam
Lower panel: gamma-velocities for the same Cepheid
Table 17. gamma-velocities of RW Cam
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
22740 1 -26.1 4.5 1 Joy (1937)
25050 340 -22.1 2.3 5 Joy (1937)
26364 288 -26.1 2.0 6 Joy (1937)
44456 160 -27.1 1.0 18 Barnes et al. (1988)
45168 223 -24.8 1.2 12 Barnes et al. (1988)
Paper III a somewhat shorter orbital period was suggested but Joy's (1937)
radial velocity measurements (see Table 17) prefer this longer value. The
amplitude of the sinusoidal O-C variation is rather large, giving rise to
considerable gamma-velocity changes. Therefore the variation in the
gamma-velocity has to be larger than it has been observed till now. The phasing
of the radial velocity data with the suspected orbital period, however,
shows that RW Cam has never been observed spectroscopically during the
phases when the Cepheid is approaching the observer. According to Figure
11, this orbital phase occurs just in the nineties, so any radial velocity
study to be performed in the near future would answer the question whether
the light-time effect interpretation is correct. If this is not the case,
the other plausible interpretation of the O-C graph would be the
occurrence of a phase jump. In any case, a regular coverage of the light
variation is also desirable.
In addition to the previously published photometric evidence, the blue
companion of RW Cam has been pointed out in the IUE spectra (Bohm-Vitense
and Proffitt, 1985).
SU Cassiopeiae
The O-C diagram of this bright Cepheid based on only photoelectric
observations is shown in Figure 12 (see also Table 18). The pulsation
period has been constant since the discovery of the light variation of SU
Cas. The current ephemeris
C = 2441645.913 + 1.949325d*E (14)
+-.003 +-.000003
is practically the same as derived in Paper I. The same conclusion has
been drawn by Rhode (1990a).
On the contrary, the study of the available radial velocity
observations gives more interesting results. SU Cas also belongs to a
binary system (Evans, 1985). This finding has been confirmed
photometrically (Usenko, 1990b): the position of SU Cas on the two-colour
diagram can be explained by assuming an A0 companion. In the light of
these facts it is worth looking for any change in the gamma-velocity of this
Cepheid (see Table 19). There are four possible values of the orbital
period: 462.5, 928, 1375 and 1682 days. Although any data set can be
folded with a "best fitting" sinusoid, and the periodicity does not
necessarily bear physical significance, the 462.5 day period seems to be
not simply an arjpgact of the data distribution. Of course, the "orbital
velocity curve" plotted in Figure 13 has to be confirmed by additional
radial velocity measurements.
Table 18. O-C residuals for SU Cas
Norm.max. E O-C W Reference
JD2400000+
30404.167 -5767 0.011 3 Walter (1943y)
30905.119 -5510 -0.013 3 Groeneveld (1944)
35755.041 -3022 -0.012 3 Prokof'yeva (1961)
36121.522* -2834 -0.004 3 Bahner & Mavridis (1977)
36199.516 -2794 0.017 2 Svolopoulos (1960)
36836.942 -2467 0.014 2 Bahner et al. (1962)
37439.297 -2158 0.027 3 Mitchell et al. (1964)
38384.671 -1673 -0.021 3 Wisniewski & Johnson (1968)
39055.269 -1329 0.009 3 Milone (1970)
39361.299 -1172 -0.005 3 Takase (1969)
39447.074 -1128 0.000 3 Wamsteker (1972)
39751.198 -972 0.029 2 Sudzius (1969)
39864.198 -914 -0.032 3 Reed (1968)
40180.041* -752 0.020 2 Feltz & McNamara (1980)
40963.647* -350 -0.002 3 Feltz & McNamara (1980)
41645.925 0 0.012 3 Szabados (1977)
41930.480 146 -0.034 3 Gieren (1976)
43347.688* 873 0.014 3 Niva & Schmidt (1979)
43690.749* 1049 -0.006 3 Moffett & Barnes (1984)
44178.083* 1299 -0.003 3 Moffett & Barnes (1984)
47149.804* 2962 -0.010 3 Rhode (1990a)
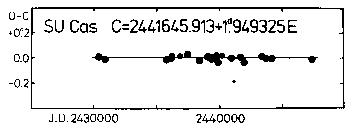
Figure 12. O-C diagram of SU Cas
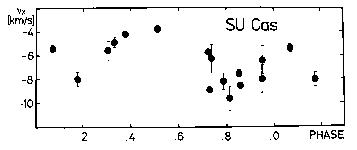
Figure 13. gamma-velocity values of SU Cas folded with the 462.5 day period
Table 19. gamma-velocities of SU Cas
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
20229 162 -6.3 1.2 4 Adams & Shapley (1918)
21252 153 -8.0 1.2 4 Adams & Shapley (1918)
34307 17 -8.0 0.6 4 Abt (1959)
34621 23 -8.5 0.3 14 Abt (1959)
35051 1 -8.2 0.7 3 Abt (1959)
36451 1 -9.6 1.0 1 Abt (1959)
40943 47 -3.8 0.3 7 Niva & Schmidt (1979)
41962 29 -8.9 0.1 63 Gieren (1976)
43406 3 -7.5 0.1 27 Niva & Schmidt (1979)
43453 59 -6.4 1.2 12 Wilson et al. (1989)
43810 28 -5.7 0.1 51 Beavers & Eitter (1986)
44079 264 -5.6 0.8 23 Barnes et al. (1987)
44574 46 -4.2 0.2 14 Haupl (1988)
44895 54 -5.4 0.3 11 Haupl (1988)
46866 1 -4.9 0.4 2 Samus (1990)
SZ Cassiopeiae
The very rapid increase in the pulsation period of SZ Cas has
been continuing (see Figure 14). The O-C diagram based on the
photoelectric O-C residuals, however, results in an ephemeris slightly
different from that determined in Paper III. The O-C residuals listed in
Table 20 have been obtained using the new elements:
C = 2443817.978 + 13.636857d*E (15)
+-.029 +-.000305
The value of the period as a function of the epoch elapsed can be given as
follows:
P = 13.636857d + 18.72*E*10^-6 (16)
+-.000305 +-1.37
Coker et al. (1989) obtained very accurate radial velocity
measurements on SZ Cas, resulting in one of the best radial velocity
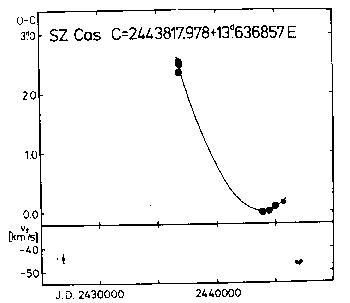
Figure 14. Upper panel: O-C diagram of SZ Cas
Lower panel: gamma-velocities for the same Cepheid
Table 20. O-C residuals for SZ Cas
Norm.max. E O-C W Reference
JD2400000+
36824.793 -513 2.523 3 Oosterhoff (1960)
36838.243 -512 2.336 3 Weaver et al. (1960)
36892.930 -508 2.475 3 Bahner et al. (1962)
43817.966 0 -0.012 3 Szabados (1981)
44404.379* 43 0.016 3 Moffett & Barnes (1984)
44963.567* 84 0.093 3 Moffett & Barnes (1984)
45672.744* 136 0.153 2 Berdnikov (1986)
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
26892 488 -43.8 1.8 7 Joy (1937)
46794 91 -46.5 0.1 24 Coker et al. (1989)
47024 47 -46.9 0.1 26 Coker et al. (1989)
47194 94 -46.3 0.1 20 Coker et al. (1989)
Table 21. gamma-velocities of SZ Cas
curves ever observed for a Cepheid. There is a hint that the y-velocity
slightly varies from year to year (see Table 21), but further accurate
measurements are necessary to confirm this suspicion. The recent study
about the position of SZ Cas on the two-colour diagram (Usenko, 1990b)
assumes a B3 - B4 companion to this Cepheid.
BY Cassiopeiae
The new version of the O-C diagram suggests an early phase jump in
addition to the recent period change (see Table 22 and Figure 15). The
pulsation of BY Cas can be characterized with the following periods during
the various time intervals:
between J.D. 2428500 and 2432000 P = 3.221315 +-.000112 days,
between J.D. 2432000 and 2434500 P = 3.221557 +-.000104 days,
between J.D. 2435500 and 2440000 P = 3.222618 +-.000037 days,
after J.D. 2443000 P = 3.222199 +-.000031 days.
The O-C residuals have been calculated with this latter period:
C = 2441774.634 + 3.222199d*E (17)
+-.019 +-.000031
The phase jump occurring at J.D. 2432000 was as large as 0.2 day. The type
of the most recent period change is not clear yet. Further photometric
observations are necessary.
The available sporadic radial velocity observations (Joy, 1937; Scmtus,
1990) are not enough for the determination of the radial velocity curve
itself. Nevertheless, BY Cas is a promising candidate for binarity: Usenko
Table 22. O-C residuals for BY Cas
Norm.max. E O-C W Reference
JD2400000+
28563.344 -4100 -0.274 1 Parenago (1940)
29223.824 -3895 -0.345 1 Kukarkina (1954)
30480.163 -3505 -0.664 1 Satyvaldiev (1970)
30650.693 -3452 -0.910 1 Dirks & Vaucouleurs (1949)
31014.735 -3339 -0.977 1 Satyvaldiev (1970)
31781.530 -3101 -1.065 1 Ashbrook (1954)
32048.696 -3018 -1.341 1 Dirks & Vaucouleurs (1949)
32132.390 -2992 -1.425 1 Satyvaldiev (1970)
33524.240 -2560 -1.565 1 Satyvaldiev (1970)
33736.708 -2494 -1.761 1 Kukarkina (1954)
33878.460 -2450 -1.786 1 Ashbrook (1954)
34361.768 -2300 -1.808 1 Kheilo (1962)
35557.258 -1929 -1.754 1 Kheilo (1962)
35615.515 -1911 -1.497 1 Satyvaldiev (1970)
36143.784 -1747 -1.668 1 Kheilo (1962)
36820.545 -1537 -1.569 3 Oosterhoff (1960)
36827.004 -1535 -1.555 3 Weaver et al. (1960)
36843.175 -1530 -1.495 1 Kheilo (1962)
36910.801 -1509 -1.535 3 Bahner et al. (1962)
38248.220 -1094 -1.328 1 Satyvaldiev (1970)
38409.256 -1044 -1.402 3 Malik (1965)
38660.818 -966 -1.172 1 Satyvaldiev (1970)
39785.406 -617 -1.131 3 Szabados (1977)
41774.189 0 -0.445 3 Szabados (1977)
43079.635 405 0.010 2 Szabados (1977)
43456.607* 522 -0.015 2 present paper
44168.732* 743 0.004 3 present paper
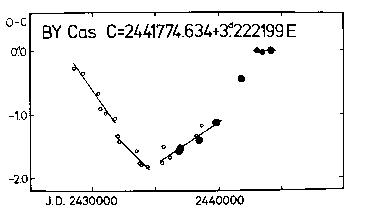
Figure 15. O-C diagram of BY Cas
(1990b) assumes a B5 photometric companion, thus supporting the earlier
suspicion published by Kurochkin (1966) and Madore and Fernie (1980). The
phase jump in the pulsation is a further evidence for duplicity.
DD Cassiopeiae
The normal light curve formed on the basis of the observations
obtained by Moffett and Barnes (1984) made the re-discussion of the
previous O-C diagram possible. According to the recent photoelectric
observations (see Table 23 and Figure 16) a period change occurred between
J.D. 2438000 and 2442500. The O-C residuals have been calculated with the
ephemeris:
C = 2442780.426 + 9.811656d*E (18)
+-.009 +-.000060
The O-C residuals based on earlier photographic observations are
compatible with the phase jump interpretation, because DD Cas was
pulsating with practically the same period between J.D. 2430000 and
2438000, the phase jump being about 0.2 day. The light-time effect
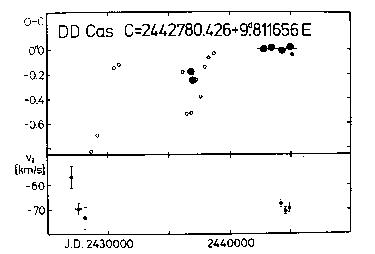
Figure 16. Upper panel: O-C diagram of DD Cas
Lower panel: gamma-velocities for the same Cepheid
Table 23. O-C residuals for DD Cas
Norm.max. E O-C W Reference
JD2400000+
17063.619 -2621 -0.457 Parenago (1940)
28601.761 -1445 -0.822 Parenago (1940)
29170.967 -1387 -0.692 Parenago (1940)
30584.392 -1243 -0.146 Solov'yov (1958)
30976.882 -1203 -0.122 Solov'yov (1958)
36137.753 -677 -0.182 Makarenko (1969)
36490.636 -641 -0.519 Makarenko (1969)
36804.942 -609 -0.185 3 Oosterhoff (1960)
36843.862 -605 -0.512 Makarenko (1969)
36932.426 -596 -0.253 3 Bahner et al. (1962)
37197.343 -569 -0.251 Makarenko (1969)
37579.865 -530 -0.383 Makarenko (1969)
37923.516 -495 -0.140 Makarenko (1969)
38296.432 -457 -0.067 Makarenko (1969)
38688.932 -417 -0.033 Makarenko (1969)
42780.422 0 -0.004 3 Szabados (1980)
43388.760* 62 0.011 3 Chekhanikhina (1982)
44252.160* 150 -0.014 3 Moffett & Barnes (1984)
44958.635* 222 0.021 3 Moffett & Barnes (1984)
45125.371* 239 -0.041 1 present paper
Table 24. gamma-velocities of DD Cas
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
26983 15 -56.5 4.5 2 Joy (1937)
27565 178 -69.5 2.3 5 Joy (1937)
28097 1 -73.3 4.5 1 Joy (1937)
44184 57 -67.5 1.6 7 Barnes et al. (1988)
44508 49 -70.6 1.3 10 Barnes et al. (1988)
44877 76 -69.1 2.0 5 Barnes et al. (1988)
suggested in Paper II cannot be responsible for the shape of the O-C
graph, since the amplitude of the wave would correspond to an enormously
massive companion.
Duplicity of DD Cas suggested by Madore (1977) and Madore and Fernie
(1980) has been checked by the radial velocity measurements, too. As Table
24 and the lower panel of Figure 16 shows, the variation in the gamma-velocity
is very probable, but further observations have to confirm the orbital
motion.
DL Cassiopeiae
The new normal light curve based on the observations obtained by
Moffett and Barnes (1984) defines the moment of light maxima more clearly
than the previously used one. Owing to the new normal curve, a systematic
correction of -0.192 day has been applied to the photoelectric O-C
residuals published in Paper II. These corrected values, together with the
more recent O-C residuals are listed in Table 25 and shown plotted in
Figure 17. The new ephemeris for calculating the moments of maxima is as
follows:
C = 2442780.172 + 5.000598d*E (19)
+-.011 +-.000022
The pulsation period of DL Cas has remained constant for the last decades,
although Meyers (1988) determined a continuously increasing period. This
latter study was based on photographic observations and, in my opinion,
Meyers' (1988) O-C diagram can be better represented with two linear
sections and a phase jump in between. The phase jump might occur at
about J.D. 2429000, therefore unnoticeable in the O-C diagrams both in
Paper II and here, in Figure 17.
Table 25. O-C residuals for DL Cas
Norm.max. E O-C W Reference
JD2400000+
36163.576 -827 -0.101 3 Arp et al. (1959)
36803.750 -747 0.025 3 Oosterhoff (1960)
37219.860 -695 0.104 2 Mitchell et al. (1964)
37947.796 -604 -0.015 2 Williams (1966)
38707.934 -509 0.066 2 Haug (1970)
42692.156* -11 -0.009 3 Szabados (1980)
43468.311* 86 0.088 1 Szabados (1980)
44292.283* 189 -0.002 3 Moffett & Barnes (1984)
44532.191* 219 -0.112 2 Eggen (1983a)
44972.332* 274 -0.004 3 Moffett & Barnes (1984)
45684.408* 363 0.019 3 Berdnikov (1986)
46284.450* 438 0.016 3 Berdnikov (1987)
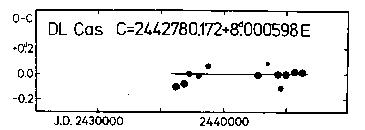
Figure 17. O-C diagram of DL Cas
The spectroscopic binary nature of DL Cas was discovered quite
recently, independently by two groups (Harris et al., 1987; Mermilliod et
al., 1987). The orbital period is rather short, at least among the Cepheid
binaries: 688.0 days (Harris et al., 1987). The orbital radial velocity
curve gives an approximate value for the amplitude of the light-time
effect in the O-C diagram. The full amplitude of this wave is about 0.02
day, therefore it can hardly be pointed out from the available photometric
data.
It is worth mentioning that DL Cas is one of the calibrating Cepheids
for the period - luminosity relationship, because this Cepheid belongs to
the open cluster NGC 129 (see Walker, 1987 and the references therein).
IX Cassiopeiae
Being a newly discovered spectroscopic binary (Harris and Welch,
1989), this Population II Cepheid would deserve more attention. The part
of the O-C diagram based on photoelectric observations is shown in Figure
18 (see also Table 26). The frequent variations in the pulsation period
are intrinsic to this star, and the straight line fit to the recent O-C
residuals:
C = 2442780.264 + 9.154549d*E (20)
+-.030 +-.000104
does not necessarily mean constancy of the period. When determining the
O-C residuals, a new normal curve based on the photometric observations
made by Harris and Welch (1989) was used. The earlier O-C residuals
have also been altered according to the new normal curve.
The radial velocity measurements of IX Cas were published by Harris
and Wallerstein (1984) and Harris and Welch (1989). Moreover, this latter
paper also deals with the determination of the orbital parameters: the
orbital period of IX Cas is 110.29 days.
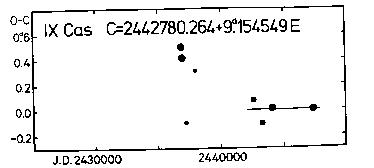
Figure 18. O-C diagram of IX Cas
Table 26. O-C residuals for IX Cas
Norm.max. E O-C W Reference
JD2400000+
36802.848 -653 0.504 3 Oosterhoff (1960)
36903.457 -642 0.413 3 Bahner et al. (1962)
37205.051 -609 -0.093 1 Mitchell et al. (1964)
37974.445 -525 0.319 1 Williams (1966)
42560.633* -24 0.078 2 Szabados (1980)
43247.037* 51 -0.109 2 Szabados (1980)
44034.452* 137 0.015 3 Harris & Welch (1989)
47348.390* 499 0.006 3 Harris & Welch (1989)
V636 Cassiopeiae
V636 Cas is one of the recently discovered Cepheid variables (Burki
and Benz, 1982), therefore it does not have a long history of
observations. The new photometric observations of this Cepheid listed in
Table 108 are differential magnitudes with respect to BD +62 259. The O-C
residuals in Table 27 and in Figure 19 (upper panel) have been calculated
using the formula:
C = 2444519.260 + 8.375735d*E (21)
+-.009 +-.000039
The number of the existing radial velocity observational series is
also small but it can be stated with certainty that the gamma-velocity of
V636 Cas is varying. In addition to the gamma-velocity values listed in Table
28, there are two more series of observations with no information about
the moment or epoch of the measurements. Redman (1930) published a single
radial velocity value of -19 km/s, being more positive than any other
velocity value published for this star. Boulon et al. (1958) gave -31 km/s
as the average of seven measurements. This latter value is even more
negative than the extreme gamma-velocity obtained from Samus' (1990) radial
velocity data. Note that the value published by Boulon et al. is probably
close to the gamma-velocity because of the short pulsation period and very
low amplitude variation. However, the companion is not bright and blue
enough to appear in the IUE spectrum of the Cepheid (Arellano Ferro and
Madore, 1986).
Table 27. O-C residuals for V636 Cas
Norm.max. E O-C W Reference
JD2400000+
41964.655* -305 -0.006 3 Burki & Benz (1982)
44519.250* 0 -0.010 3 Burki & Benz (1982)
45231.237* 85 0.040 2 present paper
47794.140* 391 -0.032 1 present paper
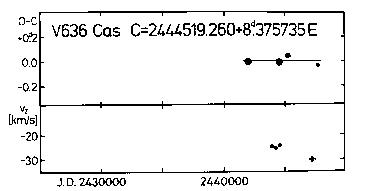
Figure 19. Upper panel: O-C diagram of V636 Cas
Lower panel: gamma-velocities for the same Cepheid
Table 28. gamma-velocities of V636 Cas
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
43855 42 -24.5 0.1 12 Burki & Benz (1982)
44201 26 -25.2 0.1 20 Burki & Henz (1982)
44558 57 -24.3 0.1 20 Burki & Benz (1982)
47282 266 -30.0 0.8 2 Samus (1990)
IR Cephei
The new photoelectric observations published here (see Table 108)
confirm the value of the pulsation period determined in Paper I. This
means that no new change has occurred in addition to that noted in Paper I
(p. 43). The O-C residuals in Table 29 and in Figure 20 have been
calculated using the equation:
C = 2441696.581 + 2.114088d*E (22)
+-.005 +-.000004
Table 29. O-C residuals for IR Cep
Norm.max. E O-C W Reference
JD2400000+
40965.096 -346 -0.011 3 Wachmann (1976)
41696.580 0 -0.001 3 Szabados (1977)
43045.394 638 0.025 2 Szabados (1977)
47413.066* 2704 -0.009 2 present paper

Figure 20. O-C diagram of IR Cep
There is only one radial velocity measurement series on IR Cep (Samus,
1990), giving -4.9 km/s for the gamma-velocity. Although the membership of IR
Cep in Cep OB2 association has been doubted on account of the age
difference between the Cepheid and the association (Kun and Szabados,
1988), it should be noted that the gamma-velocity of IR Cephei derived here
is in a good agreement with the radial velocity of some bona fide members
of Cep OB2. For example, the bright O-star, HD 206267, the most massive
member of the IC 1396 + Tr 37 complex, forming one part of Cep OB2 (Kun,
1986), has an average radial velocity of -8 km/s (Hoffleit and Jaschek,
1982).
V351 Cephei
This relatively new Cepheid variable has been observed frequently
since the discovery of its light variability (see Table 30 and Figure 21).
The pulsation period is considered to be constant during the interval of
the photoelectric observations, although Erleksova (1978) was able to
point out two major period changes on the basis of archival photographic
observations. The O-C residuals have been calculated here using a new

Figure 21. O-C diagram of V351 Cep
Table 30. O-C residuals for V351 Cep
Norm.max. E O-C W Reference
JD2400000+
42030.985 -230 -0.006 2 Percy (1975)
42676.380 0 -0.003 3 Szabados (1977)
42993.459* 113 -0.008 2 Szabados (1977)
43700.608* 365 0.016 3 Henden (1979)
44071.005* 497 0.014 3 Diethelm & Tammann (1982)
44528.380* 660 0.003 2 Eggen (1985)
44696.720* 720 -0.020 3 Arellano Ferro (1984)
normal light curve based on Arellano Ferro's (1984) observations and the
following ephemeris:
C = 2442676.383 + 2.806052d*E (23)
+-.005 +-.000010
Unfortunately no radial velocity measurements have been made on this
Cepheid so far.
X Cygni
Although X Cygni belongs to the most frequently observed Cepheids, its
O-C diagram has not yet been interpreted concordantly. The most
comprehensive analysis has been performed by Evans (1984). In the present
paper, however, I propose a new interpretation, viz. a phase jump in the
O-C diagram, that has not been mentioned in the literature on X Cygni so
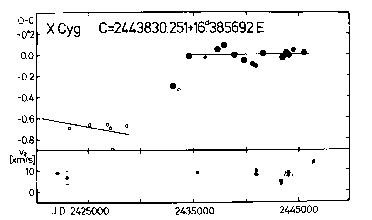
Figure 22. Upper panel: O-C diagram of X Cyg
Lower panel: gamma-velocities for the same Cepheid
Table 31. O-C residuals for X Cyg
Norm.max. E O-C W Reference
JD2400000+
17055.372 -1634 -0.658 1 Wilkens (1906)
17694.729 -1595 -0.343 1 Jordan (1919)
23183.584 -1260 -0.695 1 Henroteau (1924)
25117.137 -1142 -0.654 1 Hellerich (1935)
26804.859 -1039 -0.658 1 Kox (1935)
27148.928 -1018 -0.689 1 Dziewulski (1948)
27328.968 -1007 -0.891 1 Liau (1935)
28672.816 -925 -0.670 1 Dziewulski (1948)
33031.783 -659 -0.297 3 Eggen (1951)
33605.249 -624 -0.330 1 Romano (1951)
34605.093 -563 -0.013 3 Szabados (1981)
36096.180 -472 -0.024 1 Svolopoulos (1960)
37226.867 -403 0.050 3 Mitchell et al. (1964)
37898.718 -362 0.088 3 Williams (1966)
38881.767 -302 -0.005 3 Wisniewski & Johnson (1968)
39782.931 -247 -0.054 3 Szabados (1981)
40585.795* -198 -0.089 2 Feltz & McNamara (1980)
40929.879 -177 -0.105 2 Evans (1976)
41618.198 -135 0.015 3 Landis (1973)
43486.127* -21 -0.024 3 Moffett & Barnes (1984)
43830.274 0 0.023 3 Szabados (1981)
44092.421* 16 -0.001 3 Moffett & Barnes (1984)
44534.885* 43 0.049 2 Eggen (1983b)
45534.385* 104 0.022 3 Berdnikov (1986)
Table 32. gamma-velocities of X Cyg
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
22094 191 9.3 0.5 23 Duncan (1921)
22973 1 7.0 3.0 1 Harper (1934)
35332 21 9.5 0.2 17 Abt (1978)
40945 36 10.1 1.1 3 Schmidt (1974)
40952 169 8.2 0.3 5 Evans (1976)
43329 150 5.6 0.3 8 Beavers & Eitter (1986)
43393 49 4.2 1.1 15 Wilson et al. (1989)
44013 271 9.2 0.7 27 Barnes et al. (1987)
44055 382 7.9 0.5 18 Wallerstein (1983)
47473 1 13.9 0.7 1 Samus (1990)
far. The photoelectric O-C residuals supplemented with the early
photographic ones are listed in Table 31. After J.D. 2434000 the
photoelectric O-C residuals can be best represented by a straight line as
follows:
C = 2443830.251 + 16.385692d*E (24)
+-.011 +-.000041
As one can see in Figure 22 (the two residuals from the epoch earlier than
J.D. 2420000 have not been plotted here), the O-C residuals before J.D.
2429000 define a slightly shorter, though constant period: P = 16.385356 +-
0.000176 days. According to this interpretation the phase jump with an
amplitude of 0.8 day occurred between J.D. 2429000 and 2434000.
The gamma-velocity values of X Cyg are listed in Table 32 and shown
plotted in the lower panel of Figure 22. The variation in the gamma-velocity
seems to be larger than determined by Evans (1984) but its physical
reality cannot be supported with definitive evidence for duplicity. The
phase jump interpretation of the O-C diagram; however, implies the
duplicity of X Cyg because such phenomena only occur in binary Cepheids.
SU Cygni
The phase jump reported in Paper I is confirmed here. Because the
phase jump in the pulsation period of SU Cyg seems to be the best
documented example for this phenomenon, the whole O-C diagram has been
studied again (including the O-C diagram for the median brightness), only
omitting the very uncertain visual observations before the jump and all
visual data after the phase jump. The O-C residuals corresponding to the
maximum light, listed in Table 33, have been calculated with the current
ephemeris:
Cmax = 2441778.977 + 3.845512d*E (25)
+-.004 +-.000004
while those for the median brightness (see Table 34) have been computed as
follows:
Cmed = 2441778.616 + 3.845500d*E (26)
+-.005 +-.000010
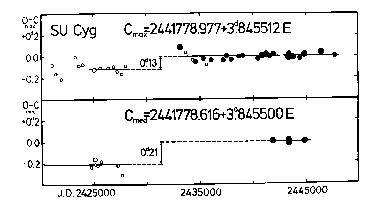
Figure 23. Upper panel: O-C diagram of SU Cyg (maximum brightness)
Lower panel: the same for the median brightness
Table 33. O-C residuals for SU Cyg (maximum brightness)
Norm.max. E O-C W Reference
JD2400000+
14256.621 -7157 -0.027 1 Muller & Kempf (1897)
14491.161 -7096 -0.063 1 Zinner (1932)
14564.221 -7077 -0.067 1 Luizet (1899)
14591.118 -7070 -0.089 1 Wendell (1913)
17052.191 -6430 -0.144 2 Wilkens (1906)
17829.048 -6228 -0.080 1 Zeipel (1908)
17882.822 -6214 -0.143 1 van der Bilt (1925)
18175.117 -6138 -0.107 1 van der Bilt (1925)
18528.908 -6046 -0.103 1 van der Bilt (1925)
19271.104 -5853 -0.091 1 van der Bilt (1925)
21086.203 -5381 -0.074 1 Luyten (1922)
21443.751 -5288 -0.159 1 Luyten (1922)
21943.616 -5158 -0.210 1 Luyten (1922)
23320.515 -4800 -0.004 1 Hellerich (1925)
23662.684 -4711 -0.086 1 Hellerich (1925)
24028.020 -4616 -0.074 1 Hellerich (1925)
25100.868 -4337 -0.123 2 Hellerich (1935)
25696.940 -4182 -0.106 1 Zverev (1936)
26423.739 -3993 -0.109 1 Zverev (1936)
26923.669 -3863 -0.095 1 Florya & Kukarkina (1953)
27277.410 -3771 -0.141 1 Florya & Kukarkina (1953)
27677.322 -3667 -0.162 1 Krebs (1935)
28050.410 -3570 -0.089 1 Krebs (1936)
33126.659 -2250 0.084 3 Eggen (1951)
33680.364 -2106 0.035 1 Chuprina (1952)
34368.640 -1927 -0.035 1 Shteiman (1958)
34591.666 -1869 -0.049 2 Szabados (1977)
35356.949 -1670 -0.023 2 Walraven et al. (1958)
35645.305 -1595 -0.080 1 Shteiman (1958)
36099.119 -1477 -0.037 2 Svolopoulos (1960)
37172.013* -1198 -0.041 2 Mitchell et al. (1964)
37498.922* -1113 0.000 2 Mitchell et al. (1964)
37941.117 -998 -0.039 2 Williams (1966)
38664.105* -810 -0.007 2 Wisniewski & Johnson (1968)
39029.433* -715 -0.003 2 Wisniewski & Johnson (1968)
40452.240* -345 -0.035 2 Feltz & McNamara (1980)
40867.591* -237 0.000 3 Evans (1976)
41225.237* -144 0.014 3 Feltz & McNamara (1980)
41540.552* -62 -0.003 2 Szabados (1977)
41932.815* 40 0.018 2 Szabados (1977)
43344.084* 407 -0.016 3 Moffett & Barnes (1984)
43367.170* 413 -0.003 3 Fernie (1979b)
43378.722* 416 0.012 2 present paper
43786.320* 522 -0.014 3 Moffett & Barnes (1984)
44474.659* 701 -0.022 2 Berdnikov & Bogdanov (1987)
44866.935* 803 0.012 3 present paper
46412.858* 1205 0.039 3 present paper
47793.366* 1564 0.008 2 present paper
The difference between the periods as determined from the various parts of
the O-C diagram (see Figure 23) is insignificant:
for the maximum brightness:
before the phase jump P = 3.845502 +- 0.000007 days
after the phase jump P = 3.845512 +- 0.000004 days,
Table 34. O-C residuals for SU Cyg (median brightness)
Norm.max. E O-C W Reference
JD2400000+
14590.722 -7070 -0.209 1 Wendell (1913)
17051.794 -6430 -0.257 2 Wilkens (1906)
17828.641 -6228 -0.201 1 Zeipel (1908)
24738.969 -4431 -0.237 1 Moncibowitz (1938)
25100.518 -4337 -0.165 2 Hellerich (1935)
25131.234 -4329 -0.213 1 Moncibowitz (1938)
25323.499 -4279 -0.223 1 Moncibowitz (1938)
25696.552 -4182 -0.183 1 Zverev (1936)
27277.010 -3771 -0.226 1 Florya & Kukarkina (1953)
27676.857 -3667 -0.311 1 Krebs (1935)
41778.619 0 0.003 3 Szabados (1977)
43343.719* 407 -0.016 3 Moffett & Barnes (1984)
43366.817* 413 0.010 3 Fernie (1979b)
44866.555* 803 0.003 3 present paper
for the median brightness:
before the phase jump P = 3.845502 +- 0.000011 days
after the phase jump P = 3.845500 +- 0.000010 days.
(Note that the O-C residuals before J.D. 2420000 listed in the respective
tables do not appear in Figure 23.) The amount of the phase jump, however,
clearly differs if the two O-C diagrams are compared. The phase jump is
0.13 day for the maximum brightness, while the value of 0.21 day can be
determined from the moments of the median brightness. This difference is a
manifestation of a noticeable change in the shape of the light curve, in
the sense that the ascending branch has become steeper since the phase
jump. The moment of the phase jump is not known yet: it might occur
between J.D. 2428000 and 2433000.
SU Cyg belongs to the most thoroughly studied Cepheids from the
spectroscopic point of view, as well. The spectroscopic orbit was recently
published by Evans (1988), while the detailed study of the companion (a
spectroscopic binary itself) was performed by Evans and Bolton (1990).
The orbital period is too short (549.16 days) to cause noticeable light-
time effect in the O-C diagram.
SZ Cygni
The new version of the O-C diagram (see Table 35 and Figure 24) is
interpreted as one more case for a phase jump. The earlier suggestion on
the light-time effect (see Paper III) is not tenable any more because the
amplitude of the O-C wave would involve much too large orbital velocity
variations that are not observed (see below). The O-C residuals have been
calculated using the ephemeris:
C = 2443760.344 + 15.110228d*E (27)
+-.033 +-.000078
This period describes well the behaviour of the pulsation after J.D.
2430000, while before that epoch the period was 15.110536 +- 0.000161
Table 35. O-C residuals for SZ Cyg
Norm.max. E O-C W Reference
JD2400000+
14991.044 -1904 0.574 1 Williams (1900)
15973.353 -1839 0.718 1 Florya & Parenago (1933)
17499.452 -1738 0.684 1 Florya & Parenago (1933)
22667.246 -1396 0.780 1 Henroteau (1924)
30659.819 -867 0.043 1 Filin (1951)
31702.567 -798 0.185 1 Filin (1951)
32201.239 -765 0.219 1 Kulikov (1957)
32820.760 -724 0.221 1 Filin (1951)
34588.194 -607 -0.241 1 Kulikov (1957)
35389.154 -554 -0.124 1 Kulikov (1957)
36779.369 -462 -0.050 3 Oosterhoff (1960)
36794.540 -461 0.011 3 Weaver et al. (1960)
37217.632 -433 0.017 2 Mitchell et al. (1964)
37942.574 -385 -0.332 1 Girnyak (1971)
38229.979 -366 -0.022 3 Kwee & Braun (1967)
39302.479 -295 -0.348 1 Girnyak (1971)
43760.486 0 0.142 3 Szabados (1981)
44349.673* 39 0.030 3 Moffett & Barnes (1984)
44999.388* 82 0.005 3 Moffett & Barnes (1984)
45603.789* 122 -0.003 3 Berdnikov (1986)
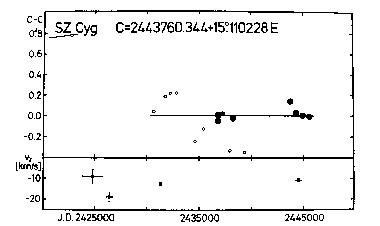
Figure 24. Upper panel: O-C diagram of SZ Cyg
Lower panel: gamma-velocities for the same Cepheid
Table 36. gamma-velocities of SZ Cyg
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
24819 962 -8.9 3.2 3 Joy (1937)
26435 231 -18.7 2.3 5 Joy (1937)
31304 7 -12.2 0.8 17 Struve (1945)
44529 309 -10.7 0.9 21 Barnes et al. (1988)
days. The phase jump was as large as 0.8 day (or about 0.05 pulsation
period). The visual observations also support the occurrence of a phase
jump at about J.D. 2430000. Nevertheless, these low quality observations
have not been taken into account in the line fitting procedure.
The analysis of the available radial velocity data leads to the
conclusion that the gamma-velocity of SZ Cyg is variable (see Table 36) but
further spectroscopic observations are desirable in order to point out
definitely the effect of the hypothetical B4 photometric companion (Madore,
1977).
TX Cygni
The recent photoelectric observations clearly show the major period
change suspected in Paper III. Both the recent value of the pulsation
period and the moment of the sudden increase can be determined from the
available data. The O-C residuals listed in Table 37 (see also Figure 25)
can be represented with the elements:
C = 2443795.007 + 14.711635d*E (28)
+-.019 +-.000272
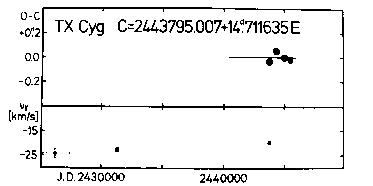
Figure 25. Upper panel: O-C diagram of TX Cyg
Lower panel: gamma-velocities for the same Cepheid
Table 37. O-C residuals for TX Cyg
Norm.max. E O-C W Reference
JD2400000+
43794.971 0 -0.036 3 Szabados (1981)
44339.391* 37 0.054 3 Moffett & Barnes (1984)
45001.361* 82 0.000 3 Moffett & Barnes (1984)
45545.668* 119 -0.024 2 Berdnikov (1986)
Table 38. gamma-velocities of TX Cyg
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
26188 1256 -24.4 1.8 7 Joy (1937)
31306 6 -22.5 0.8 14 Struve (1945)
43741 1 -19.6 0.3 1 Harris et al. (1979)
Combining the above elements with those published in Paper III, the change
in the period occurred at about J.D. 2440500. Since the period valid
previously was 14.708157 days, the difference (0.024 per cent) is
unusually large for a classical Cepheid. It is interesting to note that
Kovacs et al. (1990) determined a value of 14.1369 days for the period on
the basis of the available radial velocity data. None of the recent
photoelectric observational series, however, supports a period as short as
this.
The gamma-velocity of TX Cyg may be variable (see Table 38) but further
observations are necessary to confirm this suspicion.
VZ Cygni
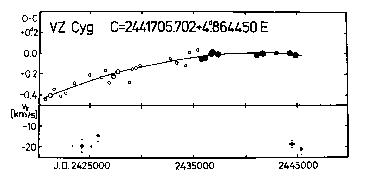
Figure 26. Upper panel: O-C diagram of VZ Cyg
Lower panel: gamma-velocities for the same Cepheid
The plot of O-C residuals supplemented with the data derived from the
recently published photoelectric observations (see Table 39 and Figure 26)
can best be represented with a parabola, indicating a continuous period
decrease. The O-C residuals have been calculated as follows:
C = 2441705.702+ 4.864450d*E (12)
+-.007 +-.000008
The value of the pulsation period can be calculated using the formula:
P = 4.864450d - 4.55*10^-8*E (30)
+-.000008 +-.44
Table 39. O-C residuals for VZ Cyg
Norm.max. E O-C W Reference
JD2400000+
20627.598 -4333 -0.442 1 Doberck (1920)
21114.079 -4233 -0.406 2 Jordan (1929)
21498.432 -4154 -0.345 1 Doberck (1920)
22179.388 -4014 -0.412 1 Doberck (1920)
22656.134 -3916 -0.382 1 Jordan (1929)
23507.509 -3741 -0.286 1 Nielsen (1954)
24996.109 -3435 -0.207 1 Wachmann (1935)
26163.550 -3195 -0.234 1 Wachmann (1935)
26513.862 -3123 -0.163 1 Wachmann (1935)
26898.035 -3044 -0.281 1 Wachmann (1935)
27321.296 -2957 -0.227 2 Gesundheit (1938)
27739.687 -2871 -0.179 2 Gesundheit (1938)
28848.680 -2643 -0.281 1 Abidov (1963)
29096.894 -2592 -0.154 1 Abidov (1963)
29452.007 -2519 -0.145 1 Abidov (1963)
29812.004 -2445 -0.118 1 Abidov (1963)
32755.060 -1840 -0.054 1 Novikov (1951)
33387.402 -1710 -0.091 1 Abidov (1963)
34219.193 -1539 -0.120 1 Abidov (1963)
34589.022 -1463 0.010 1 Abidov (1963)
35362.501 -1304 0.042 1 Vyskupaitis (1961)
35732.104* -1228 -0.053 3 Bahner & Mavridis (1977)
36106.672* -1151 -0.048 3 Bahner & Mavridis (1977)
36773.146 -1014 -0.004 3 Weaver et al. (1960)
36802.348 -1008 0.012 3 Oosterhoff (1960)
37352.009 -895 -0.010 3 Mitchell et al. (1964)
41160.858* -112 -0.026 2 Feltz & McNamara (1980)
41525.716* -37 -0.001 2 Feltz & McNamara (1980)
41705.698 0 -0.004 3 Szabados (1977)
43062.886 279 0.002 2 Szabados (1977)
44366.557* 547 0.001 3 Moffett & Barnes (1984)
44911.356* 659 -0.019 3 Moffett & Barnes (1984)
Table 40. gamma-velocities of VZ Cyg
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
24235 949 -19.4 3.2 3 Joy (1937)
25819 37 -14.4 2.6 4 Joy (1937)
44489 241 -18.5 1.8 6 Barnes et al. (1988)
45342 1 -21.0 2.8 3 Barnes et al. (1988)
Variations in the gamma-velocity of VZ Cyg cannot be excluded (see Table
40) but further radial velocity measurements are necessary to make a firm
statement on this matter.
BZ Cygni
The pulsation period keeps on being constant, but its value is slightly
modified with respect to that published in Paper III. The O-C residuals
listed in Table 41 and plotted in Figure 27 can be approximated with a
line:
C = 2443774.199 + 10.142222d*E (31)
+-.032 +-.000065
As to the radial velocity measurements of BZ Cyg, a difference as
large as 20 km/s can be seen between the gamma-velocity of the available
radial velocity measurement series (see Table 42 and the lower panel of
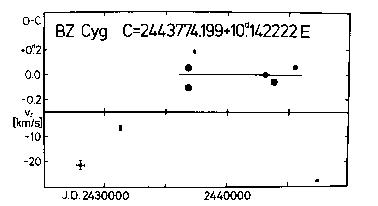
Figure 27. Upper panel: O-C diagram of BZ Cyg
Lower panel: gamma-velocities for the same cepheid
Table 41. O-C residuals for BZ Cyg
Norm.max. E O-C W Reference
JD2400000+
36786.104 -689 -0.104 3 Weaver et al. (1960)
36796.408 -688 0.058 3 Oosterhoff (1960)
37273.217 -641 0.182 1 Mitchell et al. (1964)
43013.533* -75 0.001 2 Chekhanikhina (1982)
43774.144 0 -0.055 3 Szabados (1981)
45539.006* 174 0.060 2 Berdnikov (1986)
Table 42. gamma-velocities of BZ Cyg
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
28000 312 -21.4 1.8 7 Joy (1937)
31306 6 -6.4 0.8 14 Struve (1945)
47473 1 -27.0 0.6 1 Samus (1990)
Figure 27). Since BZ Cyg is a new spectroscopic binary beyond doubt, this
Cepheid deserves immediate attention of the spectroscopists.
DT Cygni
This bright Cepheid was frequently observed photoelectrically during
the last two decades, therefore the most recent part of the O-C diagram
(see Table 43 and Figure 28) is of exceptionally good quality. Due to the
new normal light curve based on the observations obtained by Moffett and
Barnes (1984), a correction of -0.080 day has been applied to the
previously determined O-C residuals (taken from Paper I). The section of
the O-C diagram between J.D. 2440000 and 2447000 can be approximated with
the line:
C = 2441737.702 + 2.499086d*E (32)
+-.005 +-.000005
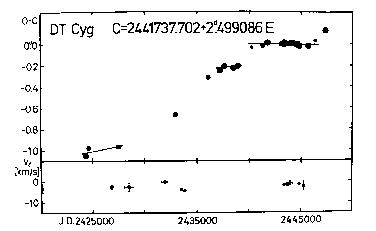
Figure 28. Upper panel: O-C diagram of DT Cyg
Lower panel: gamma-velocities for the same Cepheid
Table 43. O-C residuals for DT Cyg
Norm.max. E O-C W Reference
JD2400000+
24375.503 -6947 -1.049 3 Huffer (1928b)
24695.458 -6819 -0.977 2 Huffer (1928b)
27546.928 -5678 -0.964 2 Schneller (1936)
32975.235 -3506 -0.667 2 Eggen (1951)
36099.447 -2256 -0.317 2 Svolopoulos (1960)
37176.620 -1825 -0.250 3 Mitchell et al. (1964)
37579.011 -1664 -0.212 3 Johansen (1971)
38496.161 -1297 -0.226 3 Johansen (1971)
38871.042 -1147 -0.208 3 Wisniewski & Johnson (1968)
40185.742* -621 -0.028 1 Feltz & McNamara (1980)
41297.846* -176 -0.017 2 Feltz & McNamara (1980)
41737.718 0 0.016 3 Szabados (1977)
43044.725 523 0.001 2 Szabados (1977)
43379.606* 657 0.004 3 Moffett & Barnes (1984)
43399.611* 665 0.017 3 present paper
43754.468* 807 0.004 2 present paper
43871.925* 854 0.004 3 Moffett & Barnes (1984)
44149.328* 965 0.008 3 present paper
44534.159* 1119 -0.020 1 Eggen (1985)
44684.129* 1179 0.005 2 present paper
44869.031* 1253 -0.026 2 Arellano Ferro (1984)
45646.256* 1564 -0.017 3 Guetter & Hewitt (1984)
46341.053* 1842 0.035 1 "Carlsberg" (1989)
47343.284* 2243 0.132 3 Rhode (1990b)
Two other linear sections are also marked in the O-C graph in Figure 28,
viz.:
between J.D. 2424000 and 2428000 P = 2.499137 +- 0.000022 days, and
between J.D. 2437000 and 2439000 P = 2.499101 +- 0.000023 days.
Between the intervals of pulsating with the periods listed above, phase
jumps caused some shifts in the O-C diagram. Since the visual and the
photographic observations have not been taken into account in this study,
only the last phase jump is seen well, the amount of the jump being about
0.2 day. The suggestion put forward in Paper I (p. 49) concerning the
regular phase shift (about 0.22 day or its multiple) cannot be confirmed
here, its verification should wait until the next occurrence of the phase
jump. A new period change event can be suspected at the most recent O-C
residual in Figure 28. Further observations will clarify whether this
change will turn out to be a new phase shift. In any case, the prediction
for the moment of the light maximum near J.D. 2450000 in Table 110 may not
be accurate.
The phase jump is a characteristic feature of the binary Cepheids.
There are a few pieces of evidence concerning the duplicity of DT Cygni.
Most of them are summarized by Leonard and Turner (1986), concluding that
the existence of an early type companion is uncertain. However, according
Table 44. gamma-velocities of DT Cyg
J.D. sigma v gamma sigma n Rererence
2400000+ [d] [km/s] [km/s]
20080 29 -3.3 2.1 3 Sanford (1930)
26865 93 -2.5 0.9 12 Sanford (1930)
28519 446 -2.5 2.1 3 Young (1939)
31905 284 0.0 0.4 7 Sanford (1951)
33486 25 -3.8 0.3 11 Grassberger & Herbig (1952)
33843 24 -4.1 0.4 9 Grassberger & Herbig (1952)
43392 43 -1.7 0.6 46 Wilson et al. (1989)
43711 206 -1.7 0.2 15 Beavers & Eitter (1986)
43946 218 -0.9 0.8 23 Barnes et al. (1987)
44832 2 -1.3 0.7 6 Arellano Ferro (1984)
45270 1 -2.4 2.3 1 present paper
to a very recent paper by Usenko (1990b), DT Cyg has an A2-A3 type
photometric companion. An early evidence for the changes in the
gamma-velocity was published by Lloyd Evans (1968). His conclusion is confirmed
here (see Table 44 and Figure 28). The extreme values of the gamma-velocity
differ from each other by more than four km/s, and this difference exceeds
the observational uncertainty. New high quality radial velocity
measurements will hopefully solve the problem of duplicity of DT Cygni
because the amplitude of the expected gamma-velocity changes is rather low.
MW Cygni
The two recent O-C residuals (see Table 45 and Figure 29) indicate
that the pulsation period is slightly longer than determined in Paper II.
The O-C graph can be approximated with a line as follows:
C = 2442923.907 + 5.954666d*E (33)
+-.007 +-.000007
There is an obvious variation in the gamma-velocity of MW Cyg. According
to the data listed in Table 46, Moffett and Barnes (1987) underestimated
Table 45. O-C residuals for MW Cyg
Norm.max. E O-C W Reference
JD2400000+
30532.222 -2081 -0.025 1 Solov'yov (1946)
31038.435 -1996 0.041 1 Solov'yov (1946)
33884.781 -1518 0.057 1 Shteiman (1958)
34539.757 -1408 0.020 1 Shteiman (1958)
35677.074 -1217 -0.004 1 Shteiman (1958)
36802.499 -1028 -0.011 3 Oosterhoff (1960)
36820.339 -1025 -0.035 3 Weaver et al. (1960)
42923.911 0 0.004 3 Szabados (1980)
44364.932* 242 -0.004 3 Moffett & Barnes (1984)
44877.050* 328 0.013 3 Moffett & Barnes (1984)
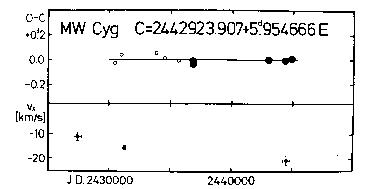
Figure 29. Upper panel: O-C diagram of MW Cyg
Lower panel: gamma-velocities for the same Cepheid
Table 46. gamma-velocities of MW Cyg
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
27487 311 -11.0 1.7 8 Joy (1937)
31304 7 -15.5 0.8 15 Struve (1945)
44514 282 -20.6 1.8 6 Barnes et al. (1988)
the difference between the gamma-velocities determined from Joy's (1937) and
their own data. While Moffett and Barnes derived -2.8 km/s, now the
difference is -9.4 km/s. The deviating result is probably caused by the
different methods in determining the gamma-velocities. In the present study
the normal radial velocity curve has been based on Struve's (1945)
measurements, and the other radial velocity measurements have been fitted
to this normal curve. MW Cyg is therefore a new spectroscopic binary
Cepheid candidate.
V386 Cygni
The O-C diagram (see Table 47 and Figure 30) confirms the earlier
conclusion (in Paper II) about the constancy of the pulsation period of
V386 Cygni. The new, slightly modified ephemeris for the moments of maxima
is as follows:
C = 2442777.141 + 5.257635d*E (34)
+-.003 +-.000004
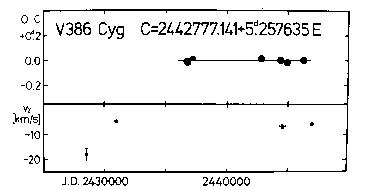
Figure 30. Upper panel: O-C diagram of V386 Cyg
Lower panel: gamma-velocities for the same Cepheid
Table 47. O-C residuals for V386 Cyg
Norm.max. E O-C W Reference
JD2400000+
36762.403 -1144 -0.004 3 Weaver et al. (1960)
36804.456 -1136 -0.012 3 Oosterhoff (1960)
37251.385 -1051 0.018 2 Mitchell et al. (1964)
42777.160 0 0.019 3 Szabados (1980)
44359.691* 301 0.002 3 Moffett & Barnes (1984)
44927.497* 409 -0.017 3 Moffett & Barnes (1984)
46289.243* 668 0.002 3 Berdnikov (1987)
Table 48. gamma-velocities of V386 Cyg
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
28571 90 -17.9 2.6 4 Joy (1937)
31006 7 -4.2 0.8 16 Struve (1945)
44581 257 -6.5 0.9 19 Barnes et al. (1988)
47010 15 -5.6 0.3 8 Metzger et al. (1990)
The study of the gamma-velocity gives a new piece of evidence for the
binary nature of V386 Cyg. It is noteworthy that there is a difference as
large as 13.7 km/s between the gamma-velocities on a time-base of about 2500
days (see Table 48 and Figure 30, lower panel). Although Moffett and
Barnes (1987) gave a smaller value for the discrepancy between the
individual gamma-velocity values, the other pieces of evidence (Kurochkin,
1966; Madore, 1977; Madore and Fernie, 1980) make the spectroscopic
binary interpretation very reasonable.
V532 Cygni
The new photoelectric observations confirm the occurrence of the phase
jump first suggested in Paper I. Because a new normal light curve was used
here, the previously determined normal maxima have been corrected by 0.102
day accordingly (see Table 49 and Figure 31). The O-C residuals have been
calculated with the elements:
C = 2441706.686 + 3.283494d*E (35)
+-.007 +-.000007
Table 49. O-C residuals for V532 Cyg
Norm.max. E O-C W Reference
JD2400000+
33889.249 -2381 0.562 1 Shteiman (1958)
34434.386 -2215 0.639 1 Shteiman (1958)
35642.593 -1847 0.520 1 Shteiman (1958)
36817.805 -1489 0.242 3 Oosterhoff (1960)
37684.512* -1225 0.106 1 Girnyak (1971)
38229.434 -1059 -0.032 3 Kwee & Braun (1967)
38439.599* -995 -0.010 1 Girnyak (1971)
39024.197* -817 0.126 1 Girnyak (1971)
39411.594* -699 0.070 1 Girnyak (1971)
41338.896* -112 -0.039 2 Feltz & McNamara (1980)
41706.661 0 -0.025 3 Szabados (1977)
43026.673 402 0.022 2 Szabados (1977)
43420.683* 522 0.013 3 present paper
44149.609* 744 0.003 2 present paper
44438.557* 832 0.004 3 Moffett & Barnes (1984)
44911.371* 976 -0.005 3 Moffett & Barnes (1984)
45009.840* 1006 -0.041 2 present paper
46490.739* 1457 0.002 2 present paper
47534.898* 1775 0.010 3 present paper
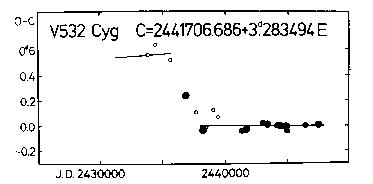
Figure 31. O-C diagram of V532 Cyg
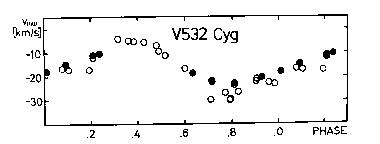
Figure 32. Radial velocity observations of V532 Cygni folded with the
3.283494 day pulsation period. Zero phase is chosen arbitrarily
at J.D. 2440000. Open circles: Barnes et al.'s (1988) data,
filled circles: Metzger et al.'s (1990) observations
This formula can be used for predicting the maxima after J.D. 2438000.
Before that epoch a phase shift occurred: between J.D. 2431200 and 2435700
the pulsation period was 3.283514 +- 0.000056 days. This latter period was
determined on the basis of the three O-C residuals listed in Table 49
supplemented with four other, less reliable O-C residuals taken from Paper
I. These low quality residuals have not been listed nor plotted here. The
phase difference, that can be seen between J.D. 2435700 and 2438000 is
about 0.58 day (= 0.18 pulsation period).
Because the phase jump is a characteristic feature of the binary
Cepheids, one expects that V532 Cygni also belongs to a binary system. In
addition to the previous photometric evidence for a B5 companion (Madore,
1977), in a more recent paper Usenko (1990b) also assumes a B7 - B8
photometric companion. The available radial velocity measurements are not
enough for the numerical determination of the gamma-velocity itself, but
the composite phase diagram of the two available radial velocity series
indicates that a shift in the gamma-velocity might occur between the epochs
of observation of the respective series. In Figure 32 open circles denote
the data obtained by Barnes et al. (1988), while Metzger et al.'s (1990)
velocity measurements are plotted as filled circles. Zero phase is
arbitrarily chosen at J.D. 2440000, and the data are folded with the
period given in Eq.(35). It is very unfortunate that Metzger et al. could
not cover the phases of least negative velocities, because the systematic
difference between the most negative values of the two radial velocity
series is clearly seen. Further photometry and spectroscopy of V532 Cygni
is extremely important.
V924 Cygni
This very low amplitude Cepheid continues to be a rather neglected
variable. The O-C residuals based on the photoelectric observations
published in the literature are listed in Table 50. These residuals have
been calculated using the elements:
C = 2443065.993 + 5.571305d*E (36)
+-.017 +-.000044
In addition to the photoelectric O-C residuals, and the line fitted to
these residuals, Figure 33 also shows another section of line
corresponding to the O-C residuals from earlier epochs. Those rather
inaccurate photographic O-C residuals are listed in Paper II, where the
deviating part was explained as a systematic difference caused by the fact
that the two sections had been obtained by different methods (because the
early photographic observations have been unpublished, and the originally
published normal maxima were used in Paper II). There is, however, another
possibility, viz. the phase jump interpretation of the O-C diagram. The
former pulsation period was 5.571106 +- 0.000029 days.
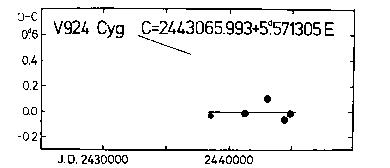
Figure 33. O-C diagram of V924 Cyg
Table 50. O-C residuals for V924 Cyg
Norm.max. E O-C W Reference
JD2400000+
38558.778 -809 -0.029 2 Eggen (1969)
41260.881 -324 -0.009 3 Wachmann (1976)
43066.098 0 0.105 3 Szabados (1980)
44391.902* 238 -0.062 3 Moffett & Barnes (1984)
44893.368* 328 -0.013 3 Moffett & Barnes (1984)
Again, the phase jump implies the existence of a companion. As to
duplicity of V924 Cygni, the only evidence is the assumption of a B8 - B9
photometric companion by Usenko (1990b). It is worth mentioning, however,
that V924 Cyg is one of the lowest amplitude Cepheids, and the extremely
low amplitude light variability can well be explained with the photometric
effect caused by the extra (and constant) light of a secondary star.
Unfortunately, no radial velocity measurements of this interesting Cepheid
have been performed yet.
V1334 Cygni
Arellano Ferro's (1984) photoelectric light curve served as the new
normal curve for determining the moments of the normal maxima. The O-C
residuals listed in Table 51 and plotted in Figure 34 have been calculated
with the elements:
C = 2441760.896 + 3.332804d*E (37)
+-.018 +-.000024
V1334 Cygni has long been known as a visual binary (ADS 14859). Now
there is growing evidence, including this paper, that the Cepheid
component of the visual pair is itself a spectroscopic binary. As to the
visual binary, Abt and Levy (1970) determined an orbital period of about
30 years from position angle measurements, while Henriksson (1982) derived
an 80 year orbital period in the same manner. The gamma-velocity data of
V1334 Cyg listed in Table 52, shown plotted in the lower panel of Figure
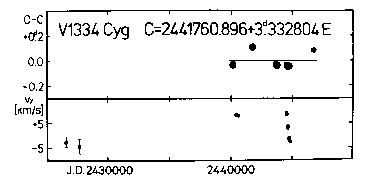
Figure 34. Upper panel: O-C diagram of V1334 Cyg
Lower panel: gamma-velocities for the same Cepheid
Table 51. O-C residuals for V1334 Cyg
Norm.max. E O-C W Reference
JD2400000+
40117.791 -493 -0.033 3 Millis (1969)
41761.010 0 0.114 3 Szabados (1977)
43657.233* 569 -0.028 3 Henden (1979)
43720.554* 588 -0.031 3 Percy et al. (1979)
44480.439* 816 -0.025 1 Parsons & Montemayor (1982)
44530.424* 831 -0.032 3 Bartolini et al. (1981)
44743.717* 895 -0.039 3 Arellano Ferro (1984)
46726.861* 1490 0.087 2 Arellano Ferro et al. (1987)
Table 52. gamma-velocities of V1334 Cyg
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
26580 5 -2.4 2.1 3 Harper (1934)
27666 7 -4.2 3.0 2 Harper (1937)
40449 35 8.4 0.2 10 Abt & Levy (1970)
40551 23 8.3 0.2 10 Abt & Levy (1970)
44536 23 8.7 0.8 5 Arellano Ferro (1984)
44672 108 3.5 1.0 2 Parsons (1983)
44747 17 -1.5 0.8 5 Arellano Ferro (1984)
44831 6 -2.5 0.5 9 Arellano Ferro (1984)
34 clearly demonstrate that the gamma-velocity varies on a much shorter
time-scale. This variation was already reported by Abt and Levy (1970) and
Henriksson (1982), but now an upper limit can be deduced for the
spectroscopic orbital period. A formal period search routine applied to
the data set resulted in 1240 days as the most reliable value of the
orbital period, but a number of other values between 500 and 1150 days
would also give a resonable preliminary orbit. The 4.5 year long orbital
period determined by Henriksson seems to be too long but the orbital
velocity amplitude derived by him (23 km/s) is confirmed here, based on the
data listed in Table 52, and one more value of the gamma-velocity, not
reported in that table, because Shajn and Albitzky (1932) published
-15.2 km/s as the average radial velocity of V1334 Cyg without reporting
the epoch of the observation. The close companion to V1334 Cyg is an
early type star: Henriksson derived a spectral type of B8III from the
ultraviolet spectrum, while Usenko (1990b) assumes a B4 photometric
companion. In the latest edition of the catalog of interferometric
measurements of binary stars McAlister and Hartkopf (1988) reported that
Yu. Balega had been able to separate the two components of the close pair
at an angular distance of 0.035 arcsecond (epoch 1986.66).
The shorter orbital period is expected to cause a light-time effect
that cannot be pointed out in the O-C diagram, but the same statement is
not valid a priori for the orbital motion of the visual pair. Therefore
regular photometric and spectroscopic observations are recommended.
V1726 Cygni
There are only two series of photoelectric observations on this
Cepheid, variability of which was only discovered in 1979. The two O-C
residuals are listed in Table 53. The moments of light maxima can be
predicted by using the following elements:
C = 2444105.697 + 4.236978d*E (38)
A very recently obtained radial velocity measurement series (Metzger
et al., 1990) gives -15.3 +- 0.3 km/s for the gamma-velocity at an epoch of
J.D. 2447002. Further observations, both photometric and spectroscopic,
are desirable.
Table 53. O-C residuals for V1726 Cyg
Norm.max. E O-C W Reference
JD2400000+
44105.697* 0 0.000 3 Platais & Shugarov (1981)
45622.535* 358 0.000 3 Berdnikov (1986)
TX Delphini
This star is one of the Population II Cepheids in this sample.
Because of its belonging to a spectroscopic binary system (Harris and
Welch, 1989), TX Del deserves a special attention. The photoelectric
observations have been analysed using a new normal light curve, based on
Moffett and Barnes' (1984) observations. The O-C graph (see Table 54 and
Figure 35) has been approximated with a straight line as follows:
C = 2442947.138 + 6.165904d*E (39)
+-.012 +-.000023
The deviations from this straight line are in some cases much larger than
expected due to the observational errors. The dashed lines in Figure 35
suggest a plausible solution to this anomaly: several successive phase
jumps might occur, similarly to the case of Y Oph (Paper IV, p. 42). The
pulsation period corresponding to the dashed lines is about 6.1664 days,
being in excellent agreement with the period valid before J.D
2436600: P = 6.166585 days (see Paper II, p. 58). Reality of the phase
jump approximation, however, has to be proven by future observations.
Table 54. O-C residuals for TX Del
Norm.max.
JD2400000+ E O-C W Reference
35665.108 -1181 -0.097 3 Walraven et al. (1958)
37293.130 -917 0.126 3 Mitchell et al. (1964)
39099.574 -624 -0.040 3 Takase (1969)
40819.978 -345 0.077 3 Pel (1976)
41929.732* -165 -0.032 3 Dean et al. (1977)
42293.514* -106 -0.038 3 Dean et al. (1977)
42361.345* -95 -0.032 3 Harris & Welch (1989)
42947.169 0 0.031 3 Szabados (1980)
43816.622* 141 0.092 3 Harris & Welch (1989)
44359.105* 229 -0.025 3 Moffett & Barnes (1984)
44457.760* 245 -0.024 2 present paper
44926.369* 321 -0.024 3 Moffett & Barnes (1984)
45549.100* 422 -0.049 1 Diethelm (1986)
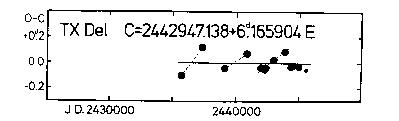
Figure 35. O-C diagram of TX Del
Because the orbital period is as short as 133.15 days (Harris and Welch,
1989), the orbital light-time effect cannot cause an observable wave in
the O-C diagram.
The radial velocity observations of TX Del are not discussed here,
because a detailed analysis was performed recently (Harris and Welch,
1989).
W Geminorum
The reliable O-C residuals from Paper II supplemented with those
obtained from the more recent photoelectric observations can be better
approximated with a parabola instead of a single sudden period decrease
suggested in Paper II. The residuals in Table 55 (see also Figure 36) have
been obtained using the equation:
C = 2442755.176 + 7.913624d*E (40)
+-.024 +-.000047
Table 55. O-C residuals for W Gem
Norm.max. E O-C W Reference
JD2400000+
14136.862 -3616 -2.650 1 Pickering (1904)
17318.675 -3214 -2.113 1 Wendell (1913)
17659.022 -3171 -2.052 1 Zeipel (1908)
17944.327 -3135 -1.638 1 van der Bilt (1926b)
18324.126 -3087 -1.693 1 van der Bilt (192ób)
18807.014 -3026 -1.536 1 van der Bilt (1926b)
19748.851 -2907 -1.420 1 van der Bilt (1926b)
24980.146 -2246 -1.030 1 Carrasco (1932)
25296.648 -2206 -1.073 2 Hellerich (1935)
25716.263 -2153 -0.831 1 Zverev (1936)
26578.991 -2044 -0.738 1 Zverev (1936)
26666.149 -2033 -0.629 1 Kukarkin (1940)
26895.429 -2004 -0.845 1 Kox (1935)
27030.096 -1987 -0.709 1 Florya & Kukarkina (1953)
29364.701 -1692 -0.623 1 Koshkina (1963)
35165.909 -959 -0.102 1 Irwin (1961)
35561.781 -909 -0.089 1 Nikulina (1959)
35569.363 -908 -0.242 2 Walraven et al. (1958)
36186.729 -830 -0.139 1 Latyshev (1969)
37270.925 -693 -0.110 3 Mitchell et al. (1964)
37927.814 -610 -0.051 1 Fridel' (1971)
39043.666 -469 -0.020 3 Wisniewski & Johnson (1963)
39083.150 -464 -0.104 3 Takase (1969)
39502.615 -411 -0.062 3 Wamsteker (1972)
39787.563 -375 -0.004 3 Szabados (1980)
40903.421* -234 0.033 2 Feltz & McNamara (1980)
40927.150 -231 0.021 3 Pel (1976)
41006.204 -221 -0.061 2 Evans (1976)
42755.172 0 -0.004 3 Szabados (1980)
43878.923* 142 0.012 3 Moffett & Barnes (1984)
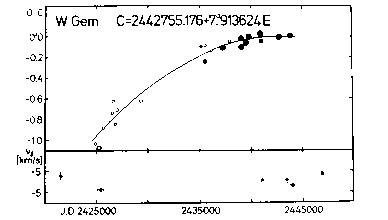
Figure 36. Upper panel: O-C diagram of W Gem
Lower panel: gamma-velocities for the same Cepheid
Table 56. gamma-velocities of W Gem
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
21600 30 3.0 1.7 4 Sanford (1930)
25468 305 -3.5 0.7 19 Sanford (1930)
41011 29 0.7 0.3 4 Evans (1976)
43445 63 0.9 1.5 8 Wilson et al. (1989)
44015 318 -1.8 0.8 24 Barnes et al. (1987)
46866 1 3.7 0.7 2 Samus (1990)
The continuous period decrease is represented with the formula:
P = 7.913624d - 3.79d*10^-7*E (41)
+-.000047 +-.29
The gamma-velocities determined for W Gem listed in Table 56 are shown
plotted in the lower panel of Figure 36. The total variation of the
gamma-velocity is larger than 7 km/s, a value far exceeding the uncertainty
due to the observational errors. Thus W Gem is a spectroscopic binary
Cepheid candidate. The information on the duplicity of W Gem is summarized
by Leonard and Turner (1986). They conclude that W Gem does not have an
early type companion. The amplitude ratios determined from the BVRI
photometry obtained by Moffett and Barnes (1984) imply a late type
companion. In any case, W Gem is a promising target for further
spectroscopic observations.
Similarly to W Gem, the new O-C diagram of this Cepheid is also
approximated with a parabola, instead of two linear sections (see Table 57
and the upper panel of Figure 37). The O-C residuals have been obtained
using the elements:
C = 2442714.955 + 5.529166d*E (42)
+-.012 +-.000015
The value of the continuously decreasing period can be calculated as
follows:
P = 5.529166d - 1.70d*10^-7*E (43)
+-.000015 +-.08
The gamma-velocity of RZ Gem shows an obvious variation (see Table 58 and
the lower panel of Figure 37). Because this variation seems to be very
rapid (i.e. the orbital period is rather short, at least for a Cepheid), a
separate gamma-velocity has been determined for each season whenever the
radial velocity of RZ Gem was measured. The formal period search routine
resulted in the value of 886 days, and this value is considered as the
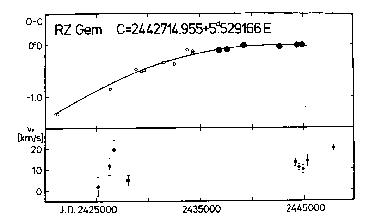
Figure 37. Upper panel: O-C diagram of RZ Gem
Lower panel: gamma-velocities for the same Cepheid
Table 57. O-C residuals for RZ Gem
Norm.max. E O-C W Reference
JD2400000+
18324.181 -4411 -1.623 1 Enebo (1909)
18832.935 -4319 -1.552 1 Enebo (1911)
21277.055 -3877 -1.323 1 Jordan (1929)
26375.422 -2955 -0.847 1 Kukarkin (1940)
28869.451 -2504 -0.472 1 Koshkina (1963)
29383.624 -2411 -0.512 1 Koshkina (1963)
29632.453 -2366 -0.495 1 Chudovicheva (1952)
31556.759 -2018 -0.339 1 Chudovicheva (1952)
32557.503 -1837 -0.374 1 Chudovicheva (1952)
33801.844 -1612 -0.095 1 Koshkina (1963)
34304.930 -1521 -0.164 1 Koshkina (1963)
34327.082 -1517 -0.128 1 Rosino & Nobili (1955)
36831.810 -1064 -0.112 3 Weaver et al. (1960)
37633.563 -919 -0.088 3 Mitchell et al. (1964)
39248.161 -627 -0.007 3 Takase (1969)
42714.927 0 -0.028 3 Szabados (1980)
44440.044* 312 -0.011 3 Moffett & Barnes (1984)
44976.380* 409 -0.004 3 Moffett & Barnes (1984)
tentative orbital period. The gamma-velocities folded with this period are
plotted in Figure 38. Zero phase is arbitrarily chosen at J.D. 2400000.
This orbital radial velocity curve is very promising, but another value
for the orbital period cannot be excluded (e.g. 930 days). Duplicity of RZ
Gem is supported by other facts, as well. Madore (1977) assumes a B5
photometric companion, and the phase-test by Madore and Fernie (1980) is
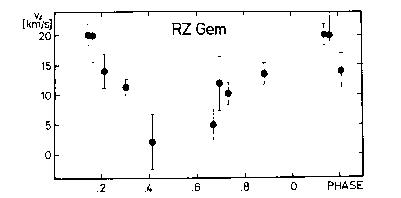
Figure 38. gamma-velocity values of RZ Gem folded with the 886 day period
Table 58. gamma-velocities of RZ Gem
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
25175 18 2.1 4.5 2 Joy (1937)
26311 1 11.9 4.5 1 Joy (1937)
26724 1 20.0 4.5 1 Joy (1937)
28058 146 5.0 2.6 4 Joy (1937)
44196 20 13.5 1.8 6 Barnes et al. (1988)
44568 43 11.3 1.3 11 Barnes et al. (1988)
44948 51 10.1 1.8 6 Barnes et al. (1988)
45373 26 14.0 2.9 3 Barnes et al. (1988)
47970 9 20.1 1.8 3 Samus (1990)
another piece of evidence for an early type companion. The discrepancy in
the gamma-velocity was already apparent in the compilation of Moffett and
Barnes (1987). New radial velocity observations would be extremely
valuable, especially because the whole orbit can be covered within three
years.
AD Geminorum
The photoelectric O-C residuals including those published in Paper I
(and modified according to the new normal light curve) have been
approximated with a constant period (see Table 59 and Figure 39):
C = 2441694.999 + 3.787990d*E (44)
+-.004 +-.000005
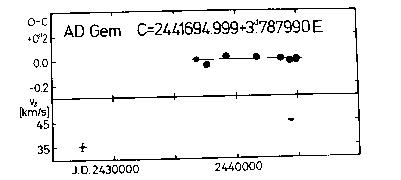
Figure 39. Upper panel: O-C diagram of AD Gem
Lower panel: gamma-velocities for the same Cepheid
Table 59. O-C residuals for AD Gem
Norm.max. E O-C W Reference
JD2400000+
36835.010 -1283 0.002 2 Weaver et al. (1960)
37630.445 -1073 -0.041 3 Mitchell et al. (1964)
39202.527 -658 0.025 3 Takase (1969)
41695.016 0 0.017 3 Szabados (1977)
43649.613* 516 0.011 3 Henden (1979)
44407.186* 716 -0.014 3 Moffett & Barnes (1984)
44960.239* 862 -0.007 3 Moffett & Barnes (1984)
44964.034* 863 0.000 3 Connolly et al. (1983)
Table 60. gamma-velocities of AD Gem
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
27438 329 35.4 1.7 8 Joy (1937)
44406 195 45.0 0.1 38 Imbert (1983)
The gamma-velocity of AD Gem may be variable (see Table 60 and the lower
panel of Figure 39). This suspicion can be supported by the facts that
Joy's (1937) radial velocity data give a deviating value from the
gamma-velocity determined from Imbert's (1983) observations, and Imbert's
radial velocity measurements themselves seem to show a systematic trend in
the sense that the more recent observations imply a more positive
gamma-velocity. Further spectroscopic study of AD Gem would be desirable.
DX Geminorum
The photographic and photoelectric O-C residuals obtained by fitting
the new normal light curve based on Moffett and Barnes' (1984)
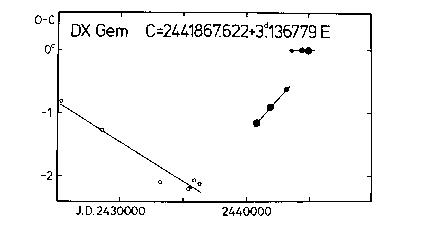
Figure 40. O-C diagram of DX Gem
Table 61. O-C residuals for DX Gem
Norm.max. E O-C W Reference
JD2400000+
25295.211 -5283 -0.808 1 Bartkus & Puchinskas (1961)
28594.649 -4231 -1.261 1 Meshkova (1940)
33182.929 -2768 -2.089 1 Satyvaldiev (1970)
35413.074 -2057 -2.194 1 Satyvaldiev (1970)
35554.252 -2012 -2.171 1 Walraven et al. (1958)
35896.275 -1903 -2.057 1 Bartkus & Puchinskas (1961)
36275.769 -1782 -2.113 1 Bartkus & Puchinskas (1961)
40793.694 -342 -1.150 3 Pel (1976)
41866.721 0 -0.901 3 Szabados (1977)
43165.632 414 -0.617 2 Szabados (1977)
43614.804* 557 -0.004 1 Henden (1979)
44439.787* 820 0.006 2 Moffett & Barnes (1984)
44954.210* 984 -0.003 3 Moffett & Barnes (1984)
observations are listed in Table 61 (see also Figure 40). The following
ephemeris was used when computing the O-C residuals:
C = 2441867.622 + 3.136779d*E (45)
+-.012 +-.000013
The photoelectric data clearly show a recent phase jump with an amplitude
of 0.2 period. This phase jump can also be suspected in the O-C diagram
based on the Sonneberg photographic observations (Hacke, 1989). Although
its scatter is very wide, Hacke's O-C diagram also shows a further period
change (after J.D. 2445000) that cannot be seen here, because no such
recent photoelectric observations are available. Consequently the
ephemeris given in Eq. (45) might not be correct for predicting the maxima
occurring even in the near future (the true period is expected to be
shorter: 3.13669 days according to Hacke). Another phase jump might occur
just before J.D. 2440500, but this phase shift cannot be traced with the
photoelectric observation. The following values of the pulsation period
can be derived from the existing data:
before J.D. 2436500 P = 3.136387 +- 0.000041 days
between J.D. 2440700 and 2443200 P = 3.137486 +- 0.000005 days
after J.D. 2443600 P = 3.136779 +- 0.000013 days.
The occurrence of the phase jump(s) in the O-C diagram of DX Gem is in
accordance with the suspected spectroscopic binary nature of this Cepheid
(Burki, 1985). Unfortunately the radial velocity data have not been
published yet.
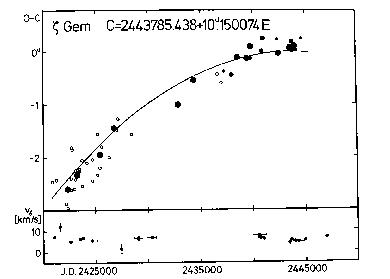
Figure 41. Upper panel: O-C diagram of Zeta Gem
Lower panel: gamma-velocities for the same Cepheid
Table 62. O-C residuals for Zeta Gem
Norm.max. E O-C W Reference
JD2300000+
96027.855 -4704 -11.635 1 Hagen (1903)
96088.465 -4698 -11.925 1 Argelander (1869)
96474.176 -4660 -11.917 1 Argelander (1869)
96565.026 -4651 -12.418 1 Hagen (1903)
97154.525 -4593 -11.623 1 Argelander (1869)
97459.537 -4563 -11.113 1 Hagen (1903)
97519.975 -4557 -11.576 1 Argelander (1869)
97875.456 -4522 -11.347 1 Argelander (1869)
98241.363 -4486 -10.843 1 Argelander (1869)
98536.305 -4457 -10.253 1 Hagen (1903)
98586.501 -4452 -10.807 1 Argelander (1869)
98982.738 -4413 -10.423 1 Argelander (1869)
99317.451 -4380 -10.663 1 Argelander (1869)
99632.685 -4349 -10.081 1 Zinner & Wachmann (1931)
99723.768 -4340 -10.349 1 Argelander (1869)
2400000+
00099.937 -4303 -9.733 1 Argelander (1869)
01927.501 -4123 -9.182 1 Argelander (1869)
02313.385 -4085 -9.001 1 Valentiner (1900)
02648.656 -4052 -8.682 1 Valentiner (1900)
02993.591 -4018 -8.850 1 Valentiner (1900)
03785.426 -3940 -8.720 1 Valentiner (1900)
03786.543 -3940 -7.603 1 Zinner & Wachmann (1931)
04090.631 -3910 -8.018 1 Valentiner (1900)
04466.252 -3873 -7.949 1 Valentiner (1900)
04608.424 -3859 -7.878 1 Zinner & Wachmann (1931)
04831.417 -3837 -8.187 1 Valentiner (1900)
05166.882 -3804 -7.674 1 Valentiner (1900)
05552.714 -3766 -7.545 1 Valentiner (1900)
05928.082 -3729 -7.730 1 Valentiner (1900)
10009.990 -3327 -6.152 1 Hagen (1891)
13564.137 -2977 -4.531 1 Plassmann (1900)
13950.417 -2939 -3.954 1 Plassmann (1900)
13979.885 -2936 -4.936 1 Pickering (1904)
14335.691 -2901 -4.382 1 Pickering (1904)
14478.219 -2887 -3.955 1 Plassmann (1900)
14487.821 -2886 -4.503 1 Wirtz (1901)
15320.879 -2804 -3.752 1 Plassmann (1900,1901,1908)
15605.224 -2776 -3.609 1 Tass (1925)
15787.268 -2758 -4.266 1 Plassmann (1908)
15787.949 -2758 -3.585 1 Nijland (1923)
15797.704 -2757 -3.980 1 Kopff (1902)
15970.085 -2740 -4.150 1 van der Bilt (1926a)
16193.288 -2723 -3.498 1 Plassmann (1908)
16172.918 -2720 -4.319 1 Lau (1909)
16406.864 -2697 -3.824 1 Gotz (1906)
16508.718 -2687 -3.471 1 Plassmann (1908)
16711.866 -2667 -3.325 1 Olivier (1952)
16721.611 -2666 -3.730 1 van der Bilt (1926a)
16874.025 -2651 -3.567 1 Tass (1925)
16874.320 -2651 -3.272 1 Tass (1925)
16883.963 -2650 -3.779 1 Plassmann (1908)
16894.896 -2649 -2.996 1 Schiller (1906)
17228.908 -2616 -3.936 1 van der Bilt (1926a)
17238.785 -2615 -4.209 1 Plassmann (1908)
Table 62. (cont.)
Norm.max. E O-C W Reference
JD2400000+
17310.450 -2608 -3.595 1 Lohnert (1909)
17594.592 -2580 -3.655 1 Olivier (1952)
17604.986 -2579 -3.411 1 Nijland (1923)
17614.853 -2578 -3.694 1 van der Bilt (1926a)
17777.885 -2562 -3.063 1 Plassmann (1908)
17939.841 -2546 -3.509 1 Nijland (1923)
17950.165 -2545 -3.335 1 van der Bilt (1926a)
18315.716 -2509 -3.186 1 Nijland (1923)
18417.041 -2499 -3.362 1 Mundler (1911)
18559.427 -2485 -3.077 1 Olivier (1952)
18640.796 -2477 -2.909 1 Nijland (1923)
19899.406 -2353 -2.908 1 Kaiser (1915)
20904.713 -2254 -2.458 1 Luyten (1922)
21320.897 -2213 -2.427 1 Luyten (1922)
22244.104 -2122 -2.877 1 Rabe (1923)
22366.187 -2110 -2.595 3 Guthnick (1921)
22375.973 -2109 -2.959 1 Bellemin (1922)
22721.639 -2075 -2.395 1 Leiner (1922)
22731.566 -2074 -2.619 1 Rabe (1923)
22732.368 -2074 -1.817 1 Gallisot (1923)
22803.383 -2067 -1.852 1 Bellemin (1922)
23056.382 -2042 -2.605 1 Rabe (1923)
23137.772 -2034 -2.415 1 Nielsen (1927a)
23168.397 -2031 -2.241 1 Zverev (1936)
23269.793 -2021 -2.345 3 Bottlinger (1928)
23442.428 -2004 -2.262 1 Leiner (1928)
23543.967 -1994 -2.223 1 Parenago (1938)
23736.995 -1975 -2.047 1 Hopmann (1926)
23797.392 -1969 -2.550 1 Leiner (1928)
24203.841 -1929 -2.104 1 Leiner (1928)
24711.413 -1879 -2.036 1 Leiner (1928)
24761.751 -1874 -2.448 1 Kukarkin (1940)
25228.769 -1828 -2.334 1 Hellerich (1935)
25280.295 -1823 -1.558 1 Leiner (1928)
25310.362 -1820 -1.941 1 Collmann (1930)
25340.804 -1817 -1.950 3 Gussow (1930)
25462.360 -1805 -2.194 1 Kukarkin (1940)
25625.169 -1789 -1.787 1 Zverev (1936)
26325.312 -1720 -1.999 1 Zverev (1936)
26802.918 -1673 -1.446 3 Hall (1934)
27056.638 -1648 -1.478 1 Florya & Kukarkina (1953)
27198.938 -1634 -1.279 1 Nielsen (1941)
28436.956 -1512 -1.570 1 Gunther (1939)
32883.249 -1074 -1.010 3 Eggen (1951)
34416.368 -923 -0.552 3 Harris (1953)
36639.347 -704 -0.439 1 Azarnova (1960a)
37004.583 -668 -0.606 1 Mayall (1964)
37258.567 -643 -0.373 1 Mitchell et al. (1964)
37979.154 -572 -0.442 2 Williams (1966)
38527.582 -518 -0.118 3 Wisniewski & Johnson (1968)
39420.773 -430 -0.133 3 Takase (1969)
39765.870 -396 -0.139 2 Sudzius (1969)
39796.556 -393 0.097 3 Szabados (1981)
40892.664* -285 -0,003 2 Feltz & McNamara (1980)
Table 62. (cont.)
Norm.max. E O-C W Reference
JD2400000+
41004.565 -274 0.247 2 Evans (1976)
42354.510 -141 0.232 1 Scarfe (1976)
42465.897 -130 -0.031 3 Depenchuk (1980)
43552.060* -23 0.074 3 Moffett & Barnes (1984)
43785.473 0 0.035 3 Szabados (1981)
43805.927 2 0.189 2 Depenchuk (1980)
44039.297* 25 0.107 3 Moffett & Barnes (1984)
44140.727* 35 0.036 1 Schmidt & Parsons (1982)
44709.348* 91 0.253 1 Ridgway et al. (1982)
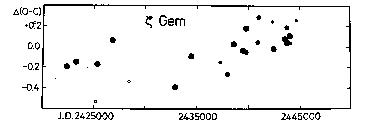
Figure 42. Delta(O-C) diagram of Zeta Gem
The old visual observations have also been taken into account during
the re-discussion of the O-C diagram, because the previous study (see Paper
III) revealed some shorter time-scale deviations superimposed on
the general parabolic trend of the O-C diagram. In order to obtain the
value of the period decrease as accurately as possible, a long time-base
data set is necessary. The currently used ephemeris is deduced from the
best parabolic fit (see Table 62 and Figure 41):
C = 2443785.438 + 10.150074d*E (46)
+-.053 +-.000053
while the continuous period decrease is as follows:
P = 10.150074d - 10.76d*10^-7*E (47)
+-.000053 +-.23
The deviations from the least squares fitted parabola are shown on the
Delta(O-C) diagram in Figure 42. Here only the photoelectric and the
photographic O-C residuals have been taken into account. The trend of the
deviations resembles the phase jump appearing in the O-C diagram of a
number of Cepheids. In most cases, however, the O-C diagrams are linear,
and Zeta Gem would be the first case when a phase jump occurs on a parabolic
O-C diagram. It cannot be excluded that this phase shift is not the
commonly appearing one in binary Cepheids, but its origin can be explained
Table 63. gamma-velocities of Zeta Gem
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
14419 170 13.5 0.8 15 Henroteau (1925)
14650 39 6.0 2.1 3 Campbell (1899)
14851 158 7.1 0.5 44 Henroteau (1925)
19799 1312 11.3 2.1 3 Spencer Jones (1928)
21014 417 7.4 0.5 42 Hase (1929)
21592 1 12.2 2.0 1 Abt (1970)
22606 188 5.1 0.6 23 Hase (1929)
23541 80 6.3 0.7 22 Jacobsen (1926)
23837 21 6.9 0.5 43 Henroteau (1925)
24664 496 5.6 0.6 25 Hase (1929)
27413 86 1.6 2.0 2 Abt (1970)
29028 393 6.5 0.9 6 Abt (1970)
30368 408 7.1 0.1 13 Scarfe (1976)
40506 636 7.8 0.1 15 Abt & Levy (1974)
40625 224 6.5 0.1 12 Scarfe (1976)
40990 21 6.2 0.3 6 Evans (1976)
43463 57 4.4 1.2 12 Wilson et al. (1989)
43619 135 5.7 0.5 4 Beavers & Eitter (1986)
43934 218 5.0 0.8 21 Barnes et al. (1987)
44313 540 4.8 0.4 19 Jacobsen & Wallerstein (1982)
44916 8 5.4 0.3 7 Beavers & Eitter (1986)
46951 296 6.7 0.4 10 Samus (1990)
in terms of the stellar activity (see Hall, 1990, and the general remarks
in this paper, on page 233).
The gamma-velocities determined from the available radial velocity data
(see Table 63 and the lower panel of Figure 41) do not show a clear
variation but changes up to 4-5 km/s cannot be excluded. Even in this
latter case, no observable light-time effect is expected in the O-C
diagram. A long series of homogeneous radial velocity observations will
hopefully solve the problem of duplicity of Zeta Gem.
V Lacertae
The photographic and photoelectric O-C residuals listed in Paper I
have been supplemented with the more recent photoelectric data. The O-C
diagram continues to be parabolic (see Figure 43). During the present
analysis the O-C residuals (listed in Table 64) have been calculated using
the elements:
C = 2441907.706 + 4.983179d*E (48)
+-.006 +-.000003
The continuous decrease in the period can be characterized as follows:
P = 4.983179d - 1.09d*10^-7*E (49)
+-.000003 +-.02
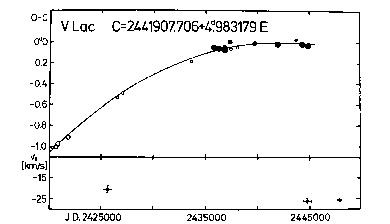
Figure 43. Upper panel: O-C diagram of V Lac
Lower panel: gamma-velocities for the same Cepheid
Table 64. O-C residuals for V Lac
Norm.max. E O-C W Reference
JD2400000+
19716.574 -4453 -1.036 1 Martin & Plummer (1916)
20070.390 -4382 -1.026 2 Martin & Plummer (1916)
20633.512 -4269 -1.003 2 Martin & Plummer (1916)
20817.920 -4232 -0.972 2 Hertzsprung (1922)
21844.515 -4026 -0.912 2 Jordan (1929)
26558.980 -3080 -0.535 1 Zonn (1933)
27092.226 -2973 -0.489 1 Zonn (1933)
33635.445 -1660 -0.184 1 Solov'yov (1952)
35788.311* -1228 -0.051 3 Bahner & Mavridis (1977)
36266.691* -1132 -0.056 3 Bahner & Mavridis (1977)
36794.894 -1026 -0.070 3 Weaver et al. (1960)
36809.829 -1023 -0.085 2 Oosterhoff (1960)
36834.777 -1018 -0.053 2 Bahner et al. (1962)
37348.104 -915 0.007 2 Mitchell et al. (1964)
37422.781 -900 -0.064 1 Golovatyj (1964)
38070.607 -770 -0.051 1 Golovatyj (1964)
39754.969 -432 -0.004 2 Szabados (1977)
41907.688 0 -0.018 3 Szabados (1977)
43711.644* 362 0.027 1 Henden (1979)
44329.517* 486 -0.014 3 Moffett & Barnes (1984)
44957.385* 612 -0.027 3 Moffett & Barnes (1984)
Because traces of a wave-like distorsion are apparently superimposed on
the fitted parabola, light-time effect was also searched for. Two possible
periods could be deduced in this way: 4020 and 8040 days. It is, however,
improbable that either of these values corresponds to the orbital period
Table 65. gamma-velocities of V Lac
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
25632 440 -20.4 1.6 9 Joy (1937)
44771 427 -26.0 1.3 11 Barnes et al. (1987)
47970 164 -25.7 0.7 8 Samus (1990)
because the waves caused by these periods are not compatible with the
gamma-velocity changes to be discussed below.
The gamma-velocities derived from the available radial velocity data are
listed in Table 65 (see also the lower panel of Figure 43). The
discrepancy noted by Moffett and Barnes (1987) is clearly seen between
Joy's (1937) and the more recent data. Nevertheless, additional radial
velocity measurements are needed to confirm the spectroscopic binary
nature of V Lac. As a matter of fact, Oosterhoff (1960) assumed a blue
photometric companion, but the spectrophotometric study performed by Miller
and Preston (1964a) does not support the existence of a blue secondary
star.
X Lacertae
The recent photoelectric data imply that the O-C diagram of X Lac can
be properly interpreted in terms of phase jumps (see Figure 44). A new
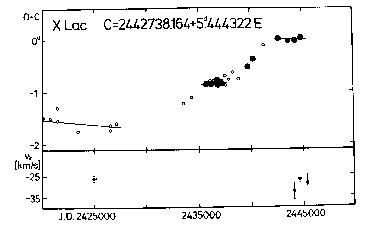
Figure 44. Upper panel: O-C diagram of X Lac
Lower panel: gamma-velocities for the same Cepheid
Table 66. O-C residuals for X Lac
Norm.max. E O-C W Reference
JD2400000+
17551.212 -4626 -1.518 1 Seares (1906,1907)
19870.408 -4200 -1.604 1 Martin & Plummer (1916)
20012.081 -4174 -1.483 1 Hertzsprung (1922)
20741.601 -4040 -1.502 1 Martin & Plummer (1916)
21460.459 -3908 -1.295 1 Hertzsprung (1922)
21487.423 -3903 -1.552 1 Jordan (1929)
23458.068 -3541 -1.752 1 Doberck (1924)
26539.666 -2975 -1.640 1 Kukarkin (1940)
26550.469 -2973 -1.726 1 Zonn (1933)
27105.928 -2871 -1.598 1 Zonn (1933)
33536.037 -1690 -1.223 1 Solov'yov (1952)
34358.247 -1539 -1.105 1 Romano (1955)
35757.696 -1282 -0.847 3 Bahner & Mavridis (1971)
36122.521 -1215 -0.792 1 Makarenko (1969)
36193.241 -1202 -0.848 3 Bahner & Mavridis (1971)
36487.298 -1148 -0.784 1 Makarenko (1969)
36786.745 -1093 -0.775 3 Weaver et al. (1960)
36797.603 -1091 -0.806 3 Oosterhoff (1960)
36835.657 -1084 -0.862 3 Bahner et al. (1962)
36841.091 -1083 -0.872 1 Makarenko (1969)
37200.493 -1017 -0.796 1 Makarenko (1969)
37216.790 -1014 -0.831 3 Mitchell et al. (1964)
37576.258 -948 -0.689 1 Makarenko (1969)
37635.956 -937 -0.878 1 Golovatyj (1964)
37946.397 -880 -0.764 1 Makarenko (1969)
38305.854 -814 -0.632 1 Makarenko (1969)
38866.704 -711 -0.754 1 Makarenko (1969)
39743.265 -550 -0.522 3 Szabados (1980)
40195.303 -467 -0.363 3 Asteriadis et al. (1977)
41333.418* -258 -0.111 1 Feltz & McNamara (1980)
42738.184 0 0.020 3 Szabados (1980)
43696.330 176 -0.034 2 Henden (1979)
44327.880* 292 -0.026 3 Moffett & Barnes (1984)
44948.587* 406 0.028 3 Moffett & Barnes (1984)
normal light curve was used during this study, and the O-C residuals
listed in Table 66 have been calculated according to the ephemeris:
C = 2442738.164 + 5.444322d*E (50)
+-.015 +-.000057
The three intervals during which the pulsation period was nearly the same
are listed below:
between J.D. 2417550 and 2427100 P = 5.444212 +- 0.000066 days
between J.D. 2435750 and 2437200 P = 5.444403 +- 0.000080 days
after J.D. 2442700 P = 5.444322 +- 0.000057 days.
The pulsation period valid during the intermediate intervals cannot be
determined reliably. The value of the phase jump was about 0.18 day (=0.15
cycle) in both cases.
The variation in the gamma-velocity can be suspected on the basis of the
radial velocity data (see Table 67 and the lower panel of Figure 44).
Table 67. gamma-velocities of X Lac
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
24959 201 -26.2 1.5 10 Joy (1937)
44061 1 -32.6 4.0 1 Barnes et al. (1988)
44608 175 -27.1 1.5 8 Barnes et al. (1988)
45340 2 -28.9 4.0 2 Barnes et al. (1988)
Moffett and Barnes (1987) also mentioned this discrepancy. There are,
however, other pieces of evidence for the binary nature of X Lac: the
method of Madore and Fernie (1980) indicated a blue photometric companion,
while Usenko (1990b) assumes a B7 companion from the two-colour diagram.
In addition, the phase jumps seen in the O-C diagram give an independent
evidence for duplicity of X Lacertae.
Y Lacertae
The new photoelectric O-C residuals confirm the earlier conclusion
about the constancy of the pulsation period of Y Lac. The new ephemeris
used for computing the O-C residuals listed in Table 68 is as follows:
C = 2441746.722 + 4.323769d*E (51)
+-.004 +-.000003
The plot of the residuals in Figure 45, however, shows hints of a
wave-like pattern with a cycle-length of more than ten thousand days.
Obviously, more observations are needed to decide whether these deviations
from the straight line can be attributed to the light-time effect or not.

Figure 45. Upper panel: O-C diagram of Y Lac
Lower panel: gamma-velocities for the same Cepheid
Table 68. O-C residuals for Y Lac
Norm.max. E O-C W Reference
JD2400000+
21658.488 -4646 -0.003 1 Jordan (1929)
21818.386 -4609 -0.085 1 Martin & Plummer (1919)
33125.147 -1994 0.020 3 Eggen (1951)
33609.468 -1882 0.079 1 Solov'yov (1952)
35710.744* -1396 0.004 3 Bahner & Mavridis (1977)
36112.859* -1303 0.008 3 Bahner & Mavridis (1977)
36834.936 -1136 0.016 3 Bahner et al. (1962)
37366.745 -1013 0.001 3 Mitchell et al. (1964)
41431.062* -73 -0.025 3 Feltz & McNamara (1980)
41746.720 0 -0.002 3 Szabados (1977)
43039.515* 299 -0.014 3 Chekhanikhina (1982)
43683.766* 448 -0.005 3 Henden (1979)
44349.632* 602 0.001 3 Moffett & Barnes (1984)
44457.722* 627 -0.003 1 present paper
44924.690* 735 -0.002 3 Moffett & Barnes (1984)
Table 69. gamma-velocities of Y Lac
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
25943 564 -19.8 1.5 10 Joy (1937)
44576 225 -22.7 0.9 21 Barnes et al. (1988)
The two gamma-velocities determined from the available radial velocity
data (see Table 69) deviate from each other. This discrepancy has been
already noted by Moffett and Barnes (1987). An A0V companion has been
discovered in an IUE spectrum (Evans et al., 1990a), thus confirming
Madore's (1977) earlier suggestion concerning the existence of a blue
companion to Y Lac. The spectroscopic binary nature of this Cepheid,
however, has to be studied further.
The recent O-C residuals confirm the parabolic shape of the O-C
diagram (see Table 70 and Figure 46). The ephemeris is slightly modified
as compared with that determined in Paper III. When constructing the
present O-C diagram, the following ephemeris was used:
C = 2442827.136 + 10.885642d*E (52)
+-.007 +-.000021
The decrease of the pulsation period is as follows:
P = 10.885642d - 6.4d*10^-8*E (53)
+-.000021 +-2.8
Because Z Lac is a member in a newly discovered spectroscopic binary
(Moffett and Barnes, 1987; Gieren, 1989a) an attempt was made to search
for a light-time effect in the O-C diagram. The only reasonable fit
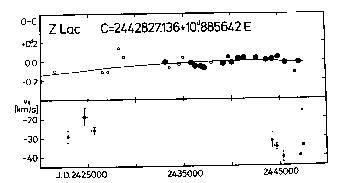
Figure 46. Upper panel: O-C diagram of Z Lac
Lower panel: gamma-velocities for the same Cepheid
Table 70. O-C residuals for Z Lac
Norm.max. E O-C W Reference
JD2400000+
20108.601 -2087 -0.200 1 Hertzsprung (1922)
21534.721 -1956 -0.099 1 Hertzsprung (1922)
26542.105 -1496 -0.111 1 Zonn (1933)
27108.157 -1444 -0.112 1 Zonn (1933)
28229.624 -1341 0.134 1 Gur'yev (1937)
28741.160 -1294 0.045 1 Gur'yev (1938)
33084.478 -895 -0.008 3 Eggen (1951)
33519.846 -855 -0.066 1 Solov'yov (1952)
34575.782 -758 -0.037 1 Chuprina (1954a)
34967.738 -722 0.036 1 Chuprina (1956)
35751.452 -650 -0.017 3 Bahner & Mavridis (1971)
36230.385 -606 -0.052 3 Bahner & Mavridis (1971)
36829.095 -551 -0.052 3 Bahner et al. (1962)
37199.191 -517 -0.068 3 Mitchell et al. (1964)
37928.575 -450 -0.022 1 Girnyak (1964)
39180.423 -335 -0.023 3 Takase (1969)
39768.312 -281 0.041 2 Szabados (1981)
40083.936 -252 -0.018 3 Asteriadis et al. (1977)
40791.548 -187 0.027 3 Asteriadis et al. (1977)
41324.953* -138 0.036 3 Feltz & McNamara (1980)
42674.769* -14 0.032 3 Szabados (1977)
43708.881* 81 0.008 3 Szabados (1977)
44318.486* 137 0.017 3 Moffett & Barnes (1984)
44938.988* 194 0.037 3 Moffett & Barnes (1984)
45679.155* 262 -0.019 3 Berdnikov (1986)
46702.305* 356 -0.120 1 "Carlsberg" (1989)
47126.952* 395 -0.013 3 Gieren (1989a)
results in a period of about, 8700 days but a period as long as this can
hardly correspond to the orbital period of the system because the
variation in the gamma-velocity suggests a much shorter value.
Table 71. gamma-velocities of Z Lac
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
22936 15 -29.1 3.2 3 Joy (1937)
24613 277 -18.7 4.5 2 Joy (1937)
25665 282 -26.0 2.0 6 Joy (1937)
44131 95 -31.7 4.0 2 Barnes et al. (1988)
44613 188 -35.0 1.6 7 Barnes et al. (1988)
45343 1 -40.4 2.8 3 Barnes et al. (1988)
47134 7 -39.9 0.3 7 Gieren (1989a)
47373 1 -16.4 0.5 1 Samus (1990)
47472 1 -34.5 0.7 1 Samus (1990)
The gamma-velocities of Z Lac are listed in Table 71. As is clearly seen
from the lower panel of Figure 46, the orbital period is much shorter than
8700 days, perhaps it can be as short as one year. Further speculation on
the value of the orbital period is untimely yet.
RR Lacertae
A new normal light curve based on Moffett and Barnes' (1984)
observations was used when studying the period changes of RR Lac. As a
consequence, a systematic correction of -0.026 day has been applied to the
normal maxima taken from Paper II. The new values of the O-C residuals
(see Table 72) have been computed with the formula:
C = 2442776.681 + 6.416289d*E (54)
+-.006 +-.000011
The best representation of the O-C plot is the approximation with a
Table 72. O-C residuals for RR Lac
Norm.max. E O-C W Reference
JD2400000+
20005.526 -3549 0.255 2 Hertzsprung (1922)
21429.895 -3327 0.208 2 Hertzsprung (1922)
21667.339 -3290 0.249 1 Jordan (1929)
26537.195 -2531 0.141 1 Zonn (1933)
27095.442 -2444 0.171 1 Zonn (1933)
32998.324 -1524 0.067 3 Eggen (1951)
33537.290 -1440 0.065 1 Solov'yov (1952)
34968.107 -1217 0.050 1 Azarnova (1957)
36033.188 -1051 0.027 3 Bahner & Mavridis (1971)
36835.212 -926 0.015 3 Bahner et al. (1962)
37213.735 -867 -0.023 3 Mitchell et al. (1964)
37579.554 -810 0.067 1 Girnyak (1964)
38240.312 -707 -0.053 1 Girnyak (1964)
40582.324 -342 0.014 3 Asteriadis et al. (1977)
42776.694 0 0.013 3 Szabados (1980)
44335.840* 243 0.001 3 Moffett & Barnes (1984)
44932.557* 336 0.003 3 Moffett & Barnes (1984)
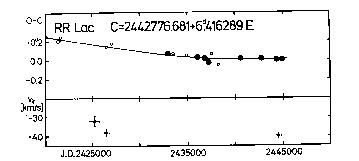
Figure 47. Upper panel: O-C diagram of RR Lac
Lower panel: gamma-velocities for the same Cepheid
Table 73. gamma-velocities of RR Lac
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
25244 526 -31.9 2.6 4 Joy (1937)
26502 255 -37.9 2.0 6 Joy (1937)
44510 288 -39.8 1.5 8 Barnes et al. (1987)
parabola (see Figure 47) indicating a continuously increasing pulsation
period:
P = 6.416289d + 4.1*10^-8*E (55)
+-.000011 +-0.6
There are three values of the gamma-velocity that can be deduced from the
published radial velocity measurements (see Table 73). These data indicate
that the gamma-velocity of RR Lac possibly varies, in accordance with the
study performed by Moffett and Barnes (1987) who also noticed the
discordant gamma-velocities. Further radial velocity observations would be
very important.
BG Lacertae
BG Lac keeps its constant pulsation period. The new value based on
solely photoelectric data (see Table 74) only slightly differs from that
determined in Paper II. The O-C residuals plotted in Figure 48 have been
approximated with the line:
C = 2442673.187 + 5.331902d*E (56)
+-.009 +-.000010
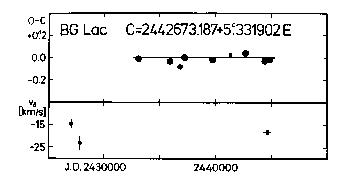
Figure 48. Upper panel: O-C diagram of BG Lac
Lower panel: gamma-velocities for the same Cepheid
Table 74. O-C residuals for BG Lac
Norm.max. E O-C W Reference
JD2400000+
33129.068 -1790 -0.014 3 Eqgen (1951)
35938.962 -1263 -0.033 3 Bahner & Mavridis (1977)
36834.834 -1095 -0.080 2 Bahner et al. (1962)
37261.307 -1015 0.001 3 Mitchell et al. (1964)
39772.614 -544 -0.018 3 Szabados (1980)
41361.567* -246 0.028 1 Feltz & McNamara (1980)
42673.231 0 0.044 3 Szabados (1980)
44400.699* 324 -0.024 3 Moffett & Barnes (1984)
44896.574* 417 -0.016 3 Moffett & Barnes (1984)
Table 75. gamma-velocities of BG Lac
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
27048 180 -14.5 2.0 6 Joy (1937)
27868 195 -23.1 3.2 3 Joy (1937)
44640 309 -18.0 0.9 23 Barnes et al. (1988)
As to the duplicity of BG Lac, Madore (1977) assumed a B8 type
photometric companion. No blue companion star was, however, found during
the IUE-study of this Cepheid (Bohm-Vitense and Proffitt, 1985).
Nevertheless, the gamma-velocity seems to be variable judging from the data
listed in Table 75. Further radial velocity measurements are necessary to
point out the possible orbital effect more clearly.
T Monocerotis
The O-C diagram of T Mon published in Paper III clearly showed a
continuous period increase during an interval of more than one century. A
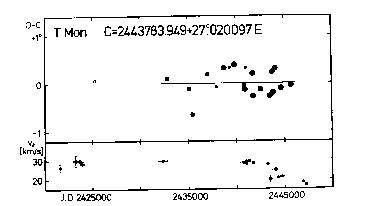
Figure 49. Upper panel: O-C diagram of T Mon
Lower panel: gamma-velocities for the same Cepheid
Table 76. O-C residuals for T Mon
Norm.max. E O-C W Reference
JD2400000+
25302.270 -684 0.067 Hellerich (1935)
32840.908 -405 0.098 2 Eggen (1951)
35191.449 -318 -0.109 2 Irwin (1961)
35488.134 -307 -0.645 2 Walraven et al. (1958)
37056.133 -249 0.188 2 Mitchell et al. (1964)
37974.560 -215 -0.068 1 Williams (1966)
38758.533 -186 0.322 3 Wisniewski & Johnson (1968)
39352.984 -164 0.331 1 Takase (1969)
39812.386 -147 0.391 3 Szabados (1981)
40892.759* -107 -0.040 2 Feltz & McNamara (1980)
40919.687 -106 -0.132 3 Pel (1976)
41001.207 -103 0.328 1 Evans (1976)
41730.626 -76 0.204 3 Landis (1976)
41757.170* -75 -0.272 3 Dean et al. (1977)
42567.909* -45 -0.136 3 Dean et al. (1977)
43513.475* -10 -0.273 3 Dean (1981)
43784.184 0 0.235 3 Szabados (1981)
43810.773* 1 -0.196 3 Moffett & Barnes (1984)
44081.479* 11 0.309 3 Eggen (1983b)
44702.532* 34 -0.100 3 Coulson & Caldwell (1985)
45702.336* 71 -0.040 3 Berdnikov (1986)
closer look at the O-C residuals revealed deviations from the uniform
period decrease (see Figure 53 in Paper III). These deviations are much
too large to be explained by the light-time effect. Because the
photoelectric O-C residuals fall on a branch of such systematic deviation,
Table 77. gamma-velocities of T Mon
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
17174 21 22.1 2.1 3 Frost (1906)
21580 30 26.2 2.0 5 Sanford (1927)
23262 268 30.0 3.0 2 Harper (1934)
23698 181 30.1 0.8 27 Sanford (1927)
23934 195 28.4 1.1 15 Sanford (1927)
32327 575 29.8 0.5 20 Sanford (1956)
40682 364 28.7 0.3 25 Wallerstein (1972)
40984 11 29.2 1.1 3 Schmidt (1974)
41006 15 28.1 0.3 4 Evans (1976)
41285 8 29.6 0.2 8 Coulson (1983)
41713 52 28.6 0.2 14 Coulson (1983)
43204 1 28.0 0.6 1 Coulson (1983)
43435 60 20.2 1.6 7 Wilson et al. (1989)
44023 314 25.0 0.8 25 Barnes et al. (1987)
44266 61 21.0 0.6 27 Coulson (1983)
44723 150 21.4 0.5 31 Coulson (1983)
46862 7 18.7 0.6 3 Samus (1990)
47134 7 17.0 0.2 13 Gieren (1989b)
the O-C diagram covering the last forty years cannot be approximated with
a parabola. Instead, a constant period has been assumed here, when
constructing the O-C diagram from the data points listed in Table 76 (and
shown plotted in Figure 49):
C = 2443783.949 + 27.020097d*E (57)
+-.048 +-.000305
Note that this ephemeris is not valid before J.D. 2425000, and the reality
of predicting future maxima using Eq. (57) may be doubted.
The duplicity of T Mon was frequently discussed in the last decade. In
the most recent detailed study Gieren (1989b) concludes that the orbital
period is about 175 years. The gamma-velocities have been redetermined in the
present study, supplemented with the results obtained from the recently
published radial velocity measurements (see Table 77 and the lower panel
of Figure 49). The new values of the gamma-velocity also confirm Gieren's
conclusion concerning the long orbital period. Although the orbital motion
of this Cepheid causes a light-time effect with a full amplitude exceeding
0.1 day, the effect cannot be pointed out in the O-C diagram because of
the wide scatter due to the long pulsation period of T Mon.
Being a possible member in the Mon OB2 association (Gieren, 1988),
T Mon can be an important calibrating Cepheid.
SV Monocerotis
The new value of the pulsation period determined only from
photoelectric data (see Table 78 and Figure 50) is somewhat shorter than
that determined in Paper III. The O-C residuals have been calculated using
the elements:
C = 2443794.249 + 15.232582d*E
+-.019 +-.000073
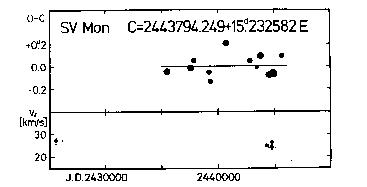
Figure 50. Upper panel: O-C diagram of SV Mon
Lower panel: gamma-velocities for the same Cepheid
Table 78. O-C residuals for SV Mon
Norm.max. E O-C W Reference
JD2400000+
35477.219 -546 -0.040 3 Walraven et al. (1958)
37564.109 -409 -0.014 3 Mitchell et al. (1964)
37899.291 -387 0.051 2 Eggen (1969)
39209.191 -301 -0.051 2 Wamsteker (1972)
39346.203 -292 -0.132 2 Takase (1969)
40732.705 -201 0.205 3 Pel (1976)
42865.108 -61 0.047 2 Dean (1977)
43489.586* -20 -0.011 1 Dean (1981)
43794.342 0 0.093 3 Szabados (1981)
44449.175* 43 -0.075 2 Eggen (1983b)
44525.339* 48 -0.074 3 Coulson & Caldwell (1985)
44890.941* 72 -0.054 3 Moffett & Barnes (1984)
44967.090* 77 -0.068 3 Coulson & Caldwell (1985)
45683.183* 124 0.094 2 Berdnikov (1986)
Table 79. gamma-velocities of SV Mon
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
25581 625 27.3 1.5 10 Joy (1937)
44264 64 24.9 0.2 26 Coulson & Caldwell (1985)
44705 370 24.2 0.9 19 Barnes et al. (1988)
44723 150 26.5 0.2 31 Coulson & Caldwell (1985)
There is no evidence for duplicity of SV Mon published in the
literature, and correspondingly, the gamma-velocities listed in Table 79
show no sign of variability.
CV Monocerotis
Considerable attention has been paid to this not very bright Cepheid,
because it is a suspected member of an anonymous open cluster (see Walker,
1987 and the references therein). Turner's (1978) photometric data were
used for determining a new normal light curve. The earlier (partly
photographic) observations have been analysed again because of the
existence of the phase jump pointed out in Paper II. The O-C residuals
listed in Table 80 have been obtained using the ephemeris:
C = 2442773.064 + 5.378804d*E (59)
+-.013 +-.000026
The O-C diagram in Figure 51 confirms the occurrence of the phase jump at
about J.D. 2436000. The shift between the two almost parallel sections is
about -0.34 day. Before J.D. 2436000 the pulsation period was 5.378757
+- 0.000011 days, i.e. practically the same value as given in the current
ephemeris (Eq. 59).
Unfortunately the observational efforts have not been extended towards
the spectroscopy of CV Mon. Only one set of radial velocity data is
available in the literature (Barnes et al., 1988). A second epoch radial
velocity observation would be extremely valuable for pointing out the
spectroscopic binary nature of this Cepheid. The companion is expected to
be a B7 star (Madore, 1977), or at least a blue one (Pel, 1978).
Table 80. O-C residuals for CV Mon
Norm.max. E O-C W Reference
JD2400000+
29805.169 -2411 0.401 1 Teplitskaya (1951)
30778.710 -2230 0.379 1 Teplitskaya (1951)
31908.250 -2020 0.371 1 Filatov (1961)
35447.480 -1362 0.347 1 Filatov (1961)
36571.216 -1153 -0.087 2 Arp (1960)
41035.782 -323 0.072 3 Pel (1976)
42773.133 0 0.069 3 Szabados (1980)
42842.984 13 -0.004 3 Turner (1978)
43886.453* 207 -0.023 2 Dean (1981)
44499.642* 321 -0.018 2 Moffett & Barnes (1984)
44951.475* 405 -0.005 3 Moffett & Barnes (1984)
45962.734* 593 0.039 1 Visvanathan (1989)
46468.211* 687 -0.091 2 present paper
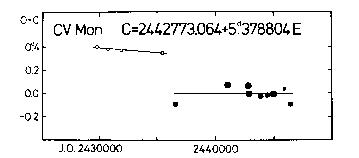
Figure 51. O-C diagram of CV Mon
V465 Monocerotis
There are only four photoelectric maxima determined for V465 Mon (see
Table 81 and Figure 52). The weighted least squares fit resulted in the
ephemeris:
C = 2441698.707 + 2.713006d*E (60)
+-.028 +-.000048
The behaviour of the pulsation period prior to J.D. 2441000 is poorly
known. As is seen in the previous O-C diagram (in Paper I), the period has
not been constant since the discovery of light variability. V465 Mon
deserves more attention. Further photometric data will hopefully explain
and remove the zero point difference between the magnitude scales used by
the three observers involved in Table 81.
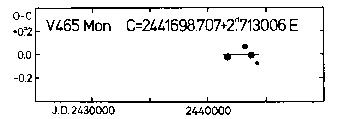
Figure 52. O-C diagram of V465 Mon
Table 81. O-C residuals for V465 Mon
Norm.max. E O-C W Reference
JD2400000+
41698.687 0 -0.020 3 Szabados (1977)
43166.515 541 0.072 2 Szabados (1977)
43676.484* 729 -0.004 3 Henden (1979)
44235.292* 935 -0.076 1 Diethelm & Tammann (1982)
According to Burki (1985) V465 Mon is a component in a spectroscopic
binary system. Unfortunately the radial velocity data have not been
published yet.
RS Orionis
The O-C diagram of RS Ori is very interesting: possibly shows both a
light-time effect and a phase jump. The photoelectric and the reliable
earlier photographic observations have been converted into O-C residuals
(see Table 82) using the ephemeris:
C = 2442820.769 + 7.566841d*E (61)
+-.009 +-.000014
Table 82. O-C residuals for RS Ori
Norm.max. E O-C W Reference
JD2400000+
16533.795 -3474 0.232 1 Kukarkina (1955)
21936.353 -2760 0.145 1 Jordan (1929)
25326.322 -2312 0.089 1 Puchinskas (1962)
26393.242 -2171 0.085 1 Martynov (1951)
27233.264 -2060 0.187 1 Martynov (1951)
27581.209 -2014 0.058 1 Puchinskas (1962)
27982.333 -1961 0.139 1 Martynov (1951)
28565.060 -1884 0.219 1 Martynov (1951)
29064.379 -1818 0.127 1 Martynov (1951)
29306.578 -1786 0.187 1 Koshkina (1963)
29798.322 -1721 0.086 1 Martynov (1951)
30751.793 -1595 0.135 1 Martynov (1951)
31039.385 -1557 0.187 1 Kukarkina (1955)
33892.019 -1180 0.122 1 Koshkina (1963)
33960.037 -1171 0.039 1 Solov'yov (1956)
35178.286 -1010 0.026 2 Irwin (1961)
35208.500 -1006 -0.027 2 Walraven et al. (1958)
36192.193 -876 -0.023 3 Bahner et al. (1977)
36282.987 -864 -0.031 1 Puchinskas (1962)
36835.395 -791 -0.003 3 Weaver et al. (1960)
37047.280 -763 0.011 3 Mitchell et al. (1964)
38076.401 -627 0.041 1 Fridel' (1971)
40777.748 -270 0.026 3 Pel (1976)
42820.794 0 0.025 3 Szabados (1980)
44440.057* 214 -0.016 3 Moffett & Barnes (1984)
44644.241* 241 -0.137 1 present paper
44795.791* 261 0.076 1 Eggen (1985)
44969.752* 284 0.000 3 Moffett & Barnes (1984)
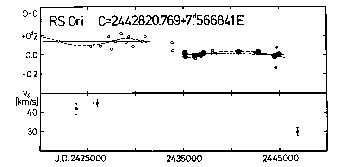
Figure 53. Upper panel: O-C diagram of RS Ori
Lower panel: gamma-velocities for the same Cepheid
Table 83. gamma-velocities of RS Ori
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
23814 66 42 3 5 Joy (1937)
26029 400 45 2 8 Joy (1937)
46866 1 30 2 2 Samus (1990)
The O-C graph in Figure 53 shows a phase jump between J.D. 2431000 and
2435000 (as already noted in Paper II). In addition to this phase shift
(of -0.13 day) a long-term sinusoidal pattern of the O-C residuals is also
suspected (see the free-hand dashed lines in Figure 53). If these waves
are attributed to the orbital motion of the Cepheid component, the phasing
of the gamma-velocity variations (see Table 83 and the lower panel of Figure
53) is in accord with the expected tendency. The wave and the rejump to
the earlier pulsation period has to be confirmed. Before J.D. 2431000 the
period was 7.566830 +- 0.000034 days. An attempt was made to approximate
the whole interval of observations with a single line. In that case,
however, the amplitude of the sinusoidal term would be too large,
therefore incompatible with the light-time interpretation.
The gamma-velocities determined for RS Ori are not accurate enough,
because no well covered pulsational radial velocity curve has been
obtained yet. Nevertheless, the variability of the gamma-velocity cannot be
doubted. Duplicity of RS Ori has been confirmed by recent IUE observations
(Evans et al., 1990a), the spectral type of the companion being B8V - B9V.
RS Orionis is a very promising target for the observers.
GQ Orionis
Using the photoelectric observations published in the last decade, the
pulsation period of GQ Ori can be refined. The O-C residuals listed in
Table 84 (see also Figure 54) have been obtained with the help of the
following ephemeris:
C = 2442798.377 + 5.616283d*E (62)
+-.011 +-.000058
The only available series of radial velocity observations (Barnes et
al., 1988) is not enough for studying the duplicity of GQ Ori.
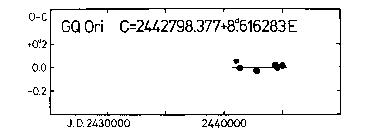
Figure 54. O-C diagram of GQ Ori
Table 84. O-C residuals for GQ Ori
Norm.max. E O-C W Reference
JD2400000+
41066.557 -201 0.053 2 Pel (1976)
41368.070 -166 -0.004 3 Wachmann (1976)
42798.348 0 -0.029 3 Szabados (1980)
44392.411* 185 0.022 3 Moffett & Barnes (1984)
44599.171* 209 -0.009 2 Eggen (1985)
44986.928* 254 0.015 3 Moffett & Barnes (1984)
The O-C residuals listed in Table 85 have been computed with the
elements:
C = 2443839.303 + 11.129319d*E (63)
+-.008 +-.000019
The plot of the O-C residuals in Figure 55 shows that a phase shift might
have occurred. This has been already pointed out in Paper III. The
pulsation period was 11.129027 +- 0.000183 days before J.D. 2426000, and a
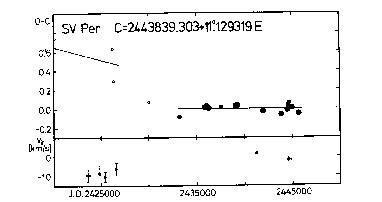
Figure 55. Upper panel: O-C diagram of SV Per
Lower panel: gamma-velocities for the same Cepheid
Table 85. O-C residuals for SV Per
Norm.max. E O-C W Reference
JD2400000+
17930.893 -2328 0.645 1 Enebo (1908)
18298.108 -2295 0.592 1 Enebo (1909)
18977.140 -2234 0.736 1 Enebo (1914)
20112.339 -2132 0.744 1 Enebo (1914)
26288.996 -1577 0.629 1 Kukarkin (1940)
26377.692 -1569 0.291 1 Rugemer (1932)
30027.889 -1241 0.071 Mergentaler (1948)
33232.980 -953 -0.082 2 Eggen et al. (1957)
35848.470 -718 0.018 3 Bahner & Mavridis (1977)
36260.245 -681 0.008 3 Bahner & Mavridis (1977)
37595.773 -561 0.018 2 Mitchell et al. (1964)
39075.985 -428 0.030 3 Takase (1969)
39209.541 -416 0.035 3 Wamsteker (1972)
41913.906 -173 -0.025 3 Vasil'yanovskaya (1977)
43839.246 0 -0.057 3 Szabados (1981)
44473.663* 57 -0.011 3 Moffett & Barnes (1984)
44529.365* 62 0.044 2 Eggen (1983b)
44651.810* 73 0.067 2 present paper
44963.375* 101 0.011 3 Moffett & Barnes (1984)
45686.725* 166 -0.045 3 Berdnikov (1986)
phase shift of about -0.3 day might occur between J.D. 2426000 and
2430000. Since most of the early O-C residuals are based on visual
observations, the phase jump cannot be determined as clearly as in the
cases when more accurate observations are also available.
Table 86. gamma-velocities of SV Per
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
23635 264 -9.4 3.2 3 Joy (1937)
24822 18 -8.6 4.5 2 Joy (1937)
25413 157 -10.3 2.6 4 Joy (1937)
26572 30 -6.3 3.2 3 Joy (1937)
41252 1 1.8 0.1 3 Lloyd Evans (1984)
44586 290 -1.7 0.9 20 Barnes et al. (1988)
The gamma-velocities listed in Table 86 confirm the previous conclusion
drawn by Lloyd Evans (1984) about the spectroscopic binary nature of SV
Per. The blue companion suspected from photometry (Madore, 1977) has been
discovered in the ultraviolet spectrum of this Cepheid (Bohm-Vitense and
Proffitt, 1985). The orbital period might not be very short, because Gieren
and Brieva (1990) found no evidence for variable gamma-velocity between 1971
and 1987.
VX Persei
The old O-C residuals corrected according to the new normal curve,
supplemented with the more recent residuals (see Table 87) indicate a
changing period (see Figure 56). The new ephemeris used in the present
study is as follows:
C = 2443759.184 + 10.886972d*E (64)
+-.017 +-.000142
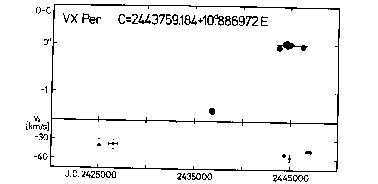
Figure 56. Upper panel: O-C diagram of VX Per
Lower panel: gamma-velocities for the same Cepheid
Table 87. O-C residuals for VX Per
Norm.max. E O-C W Reference
JD2400000+
36811.935 -638 -1.361 3 Oosterhoff (1960)
36822.785 -637 -1.398 3 Weaver et al. (1960)
43759.125 0 -0.059 3 Szabados (1981)
44358.001* 55 0.034 3 Moffett & Barnes (1984)
44532.214* 71 0.055 3 Eggen (1983b)
44651.885* 82 -0.031 2 present paper
44956.767* 110 0.016 3 Moffett & Barnes (1984)
46284.936* 232 -0.026 3 Berdnikov (1987)
Table 88. gamma-velocities of VX Per
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
25113 193 -33.3 3.2 3 Joy (1937)
26626 477 -32.4 2.6 4 Joy (1937)
44386 178 -37.0 1.0 18 Barnes et al. (1988)
44948 57 -38.4 2.0 5 Barnes et al. (1988)
46767 64 -35.3 0.1 56 Coker et al. (1989)
47004 15 -34.8 0.3 7 Metzger et al. (1990)
47124 63 -35.4 0.2 6 Coker et al. (1989)
Before J.D. 2443000 the pulsation period was longer, but an accurate value
of the period for the previous epochs cannot be determined due to the
paucity of data. A parabolic O-C graph, i.e. a continuously decreasing
period is also possible, and photometric observations to be obtained in
the near future will give a definitive answer for this problem.
The gamma-velocity of VX Per can be considered as stable (see the values
listed in Table 88). No other evidence exists for the duplicity of this
Cepheid.
AS Persei
The recent high quality photoelectric observations (especially those
obtained by Moffett and Barnes, 1984) do not support the hypothesis raised
in Paper I concerning the changing pulsational amplitude of AS Per. The O-C
residuals listed in Table 89 (see also Figure 57) have been obtained using
the elements:
C = 2441723.941 + 4.972540d*E (65)
+-.004 +-.000007
The pulsation period of AS Per has remained constant since the beginning
of the photoelectric observations.
The available radial velocity observations (Joy, 1937) are not suffi-
cient for the reliable determination of the gamma-velocity, therefore
new radial velocity observations would be valuable.
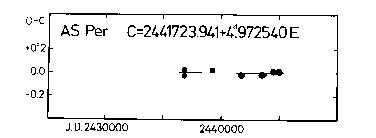
Figure 57. O-C diagram of AS Per
Table 89. O-C residuals for AS Per
Norm.max. E O-C W Reference
J.D. 2400000+.
36816.019 -987 -0.025 2 Weaver et al. (1960)
36821.041 -986 0.024 2 Oosterhoff (1960)
39252.614 -497 0.025 2 Takase (1969)
41723.922 0 -0.019 3 Szabados (1977)
43484.207* 354 -0.013 3 present paper
43688.080* 395 -0.014 2 Henden (1979)
44473.768* 553 0.012 3 Moffett & Barnes (1984)
44971.024* 653 0.014 3 Moffett & Barnes (1984)
AW Persei
This Cepheid, belonging to a wide binary system, has become a popular
object among the observers. The behaviour of AW Per is best described by
Table 90. O-C residuals for AW Per
Norm.max. E O-C W Reference
JD2400000+
29070.812 -2110 -0.021 1 Opolski (1948)
32865.073 -1523 0.094 1 Erleksova (1961)
35463.438 -1121 0.083 1 Erleksova (1961)
36109.735 -1021 -0.003 1 Erleksova (1961)
36820.711 -911 -0.004 3 Oosterhoff (1960)
36827.181 -910 0.002 3 Weaver et al. (1960)
39503.063 -496 -0.055 3 Wamsteker (1972)
40155.863* -395 -0.081 1 Feltz & McNamara (1980)
40996.175* -265 -0.040 2 Feltz & McNamara (1980)
40996.204 -265 -0.011 2 Evans (1976)
42709.062 0 -0.013 3 Szabados (1980)
43704.490* 154 0.017 3 Moffett & Barnes (1984)
44079.371* 212 0.008 3 Moffett & Barnes (1984)
44641.665* 299 -0.033 1 present paper
46477.402* 583 0.035 2 present paper
47311.211* 712 0.037 2 present paper
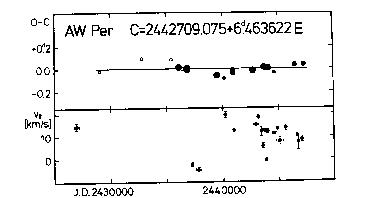
Figure 58. Upper panel: O-C diagram of AW Per
Lower panel: gamma-velocities for the same Cepheid
Table 91. gamma-velocities of AW Per
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
26981 188 14.8 1.6 9 Joy (1937)
37247 33 -2.1 0.9 8 Miller & Preston (1964b)
37798 223 -4.5 0.9 9 Miller & Preston (1964b)
40214 43 19.7 1.2 2 Welch & Evans (1989)
40971 4 12.9 0.4 3 Evans (1976)
42989 188 15.3 0.2 7 Griffin (1982) *
43155 2 18.5 1.0 2 McNamara & Chapman (1977)
43408 49 12.3 2.0 5 Wilson et al. (1989)
43559 15 6.0 1.0 2 Evans (1983)
43639 179 12.9 0.2 11 Griffin (1982) *
43821 1 -0.3 0.8 1 Beavers & Eitter (1986)
43962 220 12.3 0.8 25 Barnes et al. (1987)
44549 169 11.5 0.2 14 Griffin (1982) *
44836 159 13.4 0.4 5 Evans (1983)
45036 373 8.0 1.6 6 Barnes et al. (1987)
45610 1 13.9 1.2 1 Welch & Evans (1989)
46639 118 10.5 0.4 12 Welch & Evans (1989)
46727 1 7.5 3.4 2 present paper
47091 4 8.8 1.2 2 Welch & Evans (1989)
* Observer: T. Lloyd Evans
Welch and Evans (1989), and the additional photometric and spectroscopic
data analysed here confirm their results. The O-C residuals listed in
Table 90 have been calculated with the formula:
C = 2442709.075 + 6.463622d*E (66)
+-.007 +-.000009
The plot of the O-C residuals in Figure 58 clearly shows the wave-like
pattern due to the orbital motion. The light-time effect keeps on being
consistent with the phase of the gamma-velocity variation.
In addition to the radial velocity data analysed by Welch and Evans
(1989), Table 91 also lists some other gamma-velocity values that have not
been used for deriving the orbit of AW Persei, including that obtained
from Lloyd Evans' radial velocity measurements (Griffin, 1982), and from
the two spectra taken by the author at Rozhen Observatory (see Table 109).
The gamma-velocity values plotted in the lower panel of Figure 58 well
demonstrate the long orbital period: 13100 +- 100 days, as determined by
Welch and Evans (1989).
In view of its importance, regular photometric observations of AW Per
will continue at Konkoly.
V440 Persei
Due to the short time-base of the available photometric observations,
the shape of the O-C graph cannot be determined reliably. The O-C
residuals listed in Table 92 have been obtained using the linear ephemeris:
C = 2444551.137+ 7.572498d*E (67)
+-.014 +-.000074
Further observations are necessary to decide whether an additional
parabolic term would give a better fit when predicting the forthcoming
light maxima (cf. Figure 59).
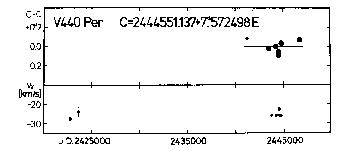
Figure 59. Upper panel: O-C diagram of V440 Per
Lower panel: gamma-velocities for the same Cepheid
Table 92. O-C residuals for V440 Per
Norm.max. E O-C W Reference
JD2400000+
41219.322* -440 0.084 2 Burki & Benz (1982)
43483.394 -141 -0.021 3 Szabados (1980)
44240.668* -41 0.003 3 Burki & Benz (1982)
44528.363* -3 -0.057 3 Eggen (1985)
44551.047* 0 -0.090 3 Burki & Benz (1982)
44869.217* 42 0.035 3 Arellano Ferro (1984)
46724.514* 287 0.070 3 Arellano Ferro et al. (1987)
Table 93. gamma -velocities of V440 Per
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
22863 107 -27.4 0.9 6 Abt (1970)
23699 28 -23.7 2.5 2 Plaskett (1934)
43796 126 -25.6 0.1 18 Burki & Benz (1982)
44202 24 -25.6 0.1 23 Burki & Benz (1982)
44525 1 -22.4 0.8 2 Beavers & Eitter (1986)
44559 67 -25.6 0.1 19 Burki & Benz (1982)
44712 136 -25.8 0.4 15 Arellano Ferro (1984)
The gamma-velocities of V440 Per are listed in Table 93. Although the
gamma-velocity seems to be constant, the variable star may have a companion,
but the inclination of the orbit is unfavourable for detecting the orbital
motion. In addition to the fact that Usenko (1990b) assumes a B8 type
photometric companion, the suspicion supporting the existence of the
companion is based on the relatively large radial velocity amplitude, as
compared with the amplitude of the light variation. It is obvious that a
companion star tends to diminish the photometric amplitude of the
variable, and does not influence the pulsational radial velocity amplitude
(i.e. having removed the orbital effect). The binary Cepheids usually have
a larger ratio of radial velocity amplitude per light variation amplitude
(Szabados, unpublished). A detailed analysis of this effect is in
progress.
S Sagittae
The reliable earlier O-C residuals taken from Paper II have been
supplemented with the O-C values derived from the more recently published
photoelectric observations (see Table 94). The O-C residuals (partly
plotted in Figure 60) have been approximated with a parabola instead of
two interesting straight lines, as suggested in Paper II. The O-C
residuals in Table 94 have been computed with the formula:
C = 2442678.821+ 5.382146d*E (68)
+-.021 +-.000029
Table 94. O-C residuals for S Sge
Norm.max. E O-C W Reference
JD2400000+
09829.793 -3919 0.602 1 Gore (1886)
09888.258 -3912 0.392 1 Gore (1886)
10164.999 -3879 0.522 1 Gore (1887)
10567.248 -3831 0.428 1 Gore (1888)
11263.052 -3748 0.514 1 Gore (1890)
11615.078 -3706 0.490 1 Gore (1891)
11975.160 -3663 0.140 1 Markwick (1892)
14196.461 -3398 0.172 1 Pickering (1904)
14934.134 -3310 0.216 1 Prittwitz (1901)
16082.542 -3173 0.270 1 Tass (1925)
16761.439 -3092 0.213 1 Lau (1907)
16803.375 -3087 0.239 1 Tass (1925)
17062.887 -3056 -0.096 1 Wilkens (1906)
17632.674 -2988 -0.295 1 Jordan (1919)
17850.862 -2962 -0.043 1 Hertzsprung (1909)
17851.029 -2962 0.124 1 Nijland (1923)
17851.054 -2962 0.149 1 Zeipel (1908)
18035.437 -2940 0.125 1 Tass (1925)
18152.813 -2926 0.151 1 Nijland (1923)
18521.561 -2882 0.085 1 Nijland (1923)
18806.555 -2848 0.086 1 Nijland (1923)
18957.443 -2830 0.095 2 Hertzsprung (1917)
19317.859 -2787 0.079 2 Hertzsprung (1917)
21061.385 -2579 0.119 1 Luyten (1922)
21488.867 -2528 0.111 1 Lacchini (1921)
21748.891 -2497 0.289 1 Luyten (1922)
22192.987 -2444 0.131 1 Leiner (1926)
22897.156 -2360 0.200 1 Eaton (1920,1921,1922)
Walker (1921,1922)
23316.013 -2310 -0.051 1 Nielsen (1927c)
23333.038 -2308 0.210 1 AFOEV (1922,1923)
24213.006 -2203 0.053 1 Parenago (1938)
24690.941 -2146 0.205 1 Leiner (1938)
24774.587 -2136 0.030 1 Kukarkin (1940)
25134.962 -2093 -0.027 1 Hellerich (1935)
25386.645 -2063 0.191 1 Leiner (1938)
25445.085 -2056 -0.044 1 Zverev (1936)
25453.702 -2055 0.191 1 Kukarkin (1940)
25797.187 -2014 0.008 1 Zverev (1936)
25847.689 -2008 0.217 1 Leiner (1938)
26182.943 -1968 0.185 1 Leiner (1938)
26384.157 -1944 0.228 1 Parenago (1938)
26451.214 -1936 0.228 1 Kukarkin (1940)
26476.126 -1933 -0.007 1 Zverev (1936)
26794.741 -1895 0.087 1 Kox (1935)
26920.633 -1880 0.246 1 Florya & Kukarkina (1953)
27591.056 -1800 0.010 1 Krebs (1935)
28001.975 -1751 0.292 1 Krebs (1936)
29091.599 -1621 0.237 1 Leiner (1938)
29141.833 -1615 0.178 3 Bennett (1939)
33131.605 -1139 0.048 3 Eggen (1951)
33198.520 -1131 -0.094 1 Solov'yov (1959)
34036.880 -1031 0.052 1 Solov'yov (1959)
34598.351 -964 -0.081 1 Solov'yov (1959)
Table 94. (cont.)
Norm.max. E O-C W Reference
JD2400000+
34615.241 -962 0.044 3 Szabados (1980)
35285.815 -882 0.047 2 Irwin (1961)
35403.191 -868 0.073 1 Solov'yov (1959)
35730.121 -829 0.099 3 Prokof'yeva (1961)
35730.154 -829 0.132 1 Solov'yov (1959)
36048.551 -791 0.007 1 Solov'yov (1959)
36190.964 -774 -0.076 1 Latyshev (1969)
36207.768 -772 -0.036 1 Svolopoulos (1960)
36450.962 -743 0.075 1 Solov'yov (1959)
36459.445 -742 0.176 1 Solov'yov (1959)
36509.621 -736 0.059 3 Walraven et al. (1958)
36718.940 -711 -0.175 1 Azarnova (1960b)
37213.656 -652 -0.006 3 Mitchell et al. (1964)
37917.700 -568 -0.062 3 Walraven et al. (1964)
39040.928 -434 -0.042 3 Wisniewski & Johnson (1968)
40440.802* -267 0.014 3 Feltz & McNamara (1980)
40834.696 -220 -0.053 2 Evans (1976)
41220.269* -174 -0.059 2 Feltz & McNamara (1980)
42595.144 -10 0.144 1 Berdnikov (1977)
42678.783 0 -0.038 3 Szabados (1980)
43340.987* 79 -0.024 3 Moffett & Barnes (1984)
43835.505* 138 -0.052 3 Moffett & Barnes (1984)
44808.023* 254 0.137 1 present paper
46643.574* 473 -0.002 2 present paper
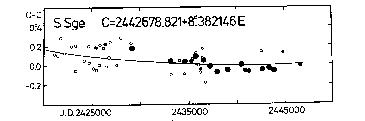
Figure 60. O-C diagram of S Sge
The continuous period increase is given by the equation:
P = 5.382146d + 4.4d*10^-8*E (69)
+-.000029 +-1.6
Future photoelectric observations are needed to decide whether the deviations
from the parabola are systematic or random. It is clear, however, that the
light-time effect expected from the orbital motion is much less than the
detection limit.
S Sge is one of the best studied binary Cepheids, therefore no attempt
was made here for determining the orbital elements. A single new radial
velocity value obtained with the 2m telescope in Rozhen is, however,
listed in Table 109. The most recent results concerning the duplicity of
S Sge are published by Slovak and Barnes (1987) (Porb = 676.2 days),
Evans et al. (1989), and Slovak et al. (1989). The two latter papers put
forward evidence for a third component in the system, what makes S Sge an
even more interesting object for future observations.
SW Tauri
The previously determined O-C residuals (see Paper I) have been
corrected according to the new normal light curve based on the superior
observations made by Moffett and Barnes (1984). The corrected and the
newly determined O-C residuals are all listed in Table 95. The plot of
these residuals in Figure 61 shows a parabolic shape instead of the
occurrence of a single period change suggested in Paper I. The new
ephemeris used when determining the O-C values is as follows:
C = 2441687.762 + 1.583577d*E (70)
+-.003 +-.000001
The continuous period decrease can be computed from the formula:
P = 1.583577d +- 7.13d*10^-9*E (71)
+-.000001 +-.54
This slight and smooth period change is atypical of the short period
Population II Cepheids.

Figure 61. Upper panel: O-C diagram of SW Tau
Lower panel: gamma-velocities for the same Cepheid
Table 95. O-C residuals for SW Tau
Norm.max. E O-C W Reference
JD2400000+
30434.681 -7106 -0.183 1 Solov'yov (1957)
32354.052 -5894 -0.107 1 Borzdyko (1965)
33638.337 -5083 -0.103 2 Eggen et al. (1957)
34377.911 -4616 -0.059 1 Borzdyko (1965)
35879.185 -3668 -0.017 1 Borzdyko (1965)
37465.873 -2666 -0.073 1 Mandel' (1970)
39059.018 -1660 -0.006 3 Milone (1970)
39078.014 -1648 -0.013 3 Wamsteker (1972)
41687.762 0 0.000 3 Szabados (1977)
42455.800* 485 0.003 3 Dean et al. (1977)
43166.821* 934 -0.002 3 Stobie & Balona (1979)
43176.324 940 0.000 2 Szabados (1977)
43630.795* 1227 -0.016 2 Henden (1979)
43675.141* 1255 -0.010 2 Diethelm & Tammann (1982)
44519.188* 1788 -0.010 3 Moffett & Barnes (1984)
44994.253* 2088 -0.018 3 Moffett & Barnes (1984)
45966.558* 2702 -0.029 2 Diethelm (1986)
46337.110* 2936 -0.034 2 Wallerstein (1987)
Table 96. gamma-velocities of SW Tau
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
24993 176 15.3 2.6 4 Joy (1937)
27343 174 14.6 2.0 6 Joy (1937)
28175 59 16.8 2.3 5 Joy (1937)
43139 26 11.5 0.6 17 Stobie & Balona (1979)
43526 1 8.0 2.5 1 Stobie & Balona (1979)
44187 29 8.6 1.6 7 Barnes et al. (1988)
44555 49 12.2 1.3 10 Barnes et al. (1988)
44948 51 8.0 1.8 6 Barnes et al. (1988)
47793 1 10.4 1.2 1 Samus (1990)
The gamma-velocity of SW Tau seems to be variable (see Table 96 and the
lower panel of Figure 61). Nevertheless, further radial velocity
observations are necessary to confirm the duplicity of this variable star.
SZ Tauri
A rejump to an earlier pulsation period was reported in Paper I. Since
then a new period change has occurred (Trammell, 1987), and interestingly
enough, the new period is almost identical with that valid during the
interval 1920 - 1960. The photoelectric O-C residuals listed in Table 97
confirm the new phase jump, though this event took place so slowly that
the intermediate period can well be determined (see Figure 62). The
current ephemeris used for calculating the O-C residuals is as follows:
C = 2441659.262 + 3.149138d*E (72)
+-.032 +-.000043
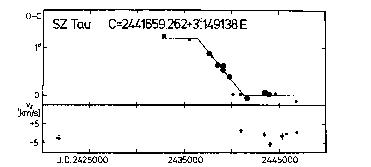
Figure 62. Upper panel: O-C diagram of SZ Tau
Lower panel: gamma-velocities for the same Cepheid
Table 97. O-C residuals for SZ Tau
Norm.max. E O-C W Reference
JD2400000+
32852.379 -2797 1.256 2 Eggen (1951)
35541.659 -1943 1.172 1 Walraven et al. (1958)
37619.809 -1283 0.891 3 Mitchell et al. (1964)
37962.988 -1174 0.814 1 Williams (1966)
38529.659 -994 0.640 3 Wisniewski & Johnson (1968)
39055.461 -827 0.536 3 Milone (1970)
39077.600 -820 0.631 3 Wamsteker (1972)
39807.965 -588 0.396 3 Szabados (1977)
40147.996* -480 0.032 1 Feltz & McNamara (1980)
40991.677* -212 0.032 1 Feltz & McNamara (1980)
41659.204 0 -0.058 3 Szabados (1977)
43520.462* 591 0.059 3 Moffett & Barnes (1984)
43926.666* 720 0.025 3 Moffett & Barnes (1984)
44647.837* 949 0.043 1 present paper
46845.772* 1647 -0.120 1 Trammell (1987)
The earlier values of the pulsation period have not been determined again,
these values are taken from Paper I:
before J.D. 2418500 P = 3.14839 days,
between J.D. 2425500 and 2436300 P = 3.149057 days,
between J.D. 2436300 and 2441300 P = 3.148380 days,
after J.D. 2441300 P = 3.149138 days.
Because of the stepwise O-C graph, i.e. the phenomenon of the phase
jump, SZ Tau probably belongs to a binary system, as well. The existence
of a bright blue companion is, however, doubtful (see Leonard and Turner,
1986, and the references therein). As can be seen in the lower panel of
Table 98. gamma-velocities of SZ Tau
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
20095 49 -3.7 0.6 30 Haynes (1914)
21784 236 -2.5 1.2 4 Abt (1970)
40972 10 1.4 0.8 5 Schmidt (1974)
43449 59 -0.3 1.4 9 Wilson et al. (1989)
44011 220 -5.5 0.8 25 Barnes et al. (1987)
45311 147 -1.3 1.5 8 Barnes et al. (1987)
45721 8 -0.1 0.1 36 Gieren (1985)
46866 1 0.9 0.5 2 Samus (1990)
Figure 62, and in the data listed in Table 98, the gamma-velocity of SZ Tau
might be variable. The spectroscopic binary nature of SZ Tau, however,
needs confirmation.
SZ Tau is an important object because of one more reason, viz. its
possible membership in the open cluster NGC 1647 (Walker, 1987; Gieren,
1988).
S Vulpeculae
S Vul is one of the longest period Cepheids in our Galaxy. Its
pulsation period has been strongly varying (Mahmoud and Szabados, 1980),
and the latest period change just noticeable in 1980 now can be traced.
The O-C residuals listed in Table 99, and shown plotted in Figure 63 have
been obtained with the elements:
C = 2444147.692+ 68.500d*E (73)
+-.518 +-.027
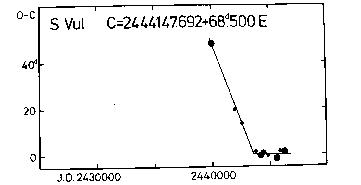
Figure 63. O-C diagram of S Vul
Table 99. O-C residuals for S Vul
Norm.max. E O-C W Reference
JD2400000+
40017.349 -61 48.157 3 Fernie (1970)
41975.061* -32 19.369 1 Schmidt (1976)
42585.601* -23 13.409 1 Dawson (1979)
43738.161 -6 1.469 1 Turner (1980)
44147.253 0 -0.439 3 Mahmoud & Szabados (1980)
44422.573 4 0.881 2 Mahmoud & Szabados (1980)
44832.141* 10 -0.551 1 present paper
45584.257* 21 -1.935 3 Berdnikov & Ivanov (1986)
45861.682* 25 1.490 1 Berdnikov & Ivanov (1986)
46272.203* 31 1.011 3 Berdnikov & Ivanov (1986)
The available radial velocity data do not permit even the reliable
determination of the gamma-velocity, but as a matter of fact, no evidence can
be found in the literature regarding the duplicity of S Vul.
T Vulpeculae
A new normal light curve has been determined on the basis of the
photoelectric observations made by Moffett and Barnes (1984). The new O-C
residuals (listed in Table 100) have been determined with the help of this
normal curve, and the O-C residuals published earlier in Paper I have been
corrected accordingly. The best linear fit to the data points after J.D.
2434500 is as follows:
C = 2441705.127 + 4.435453d*E (74)
+-.007 +-.000009
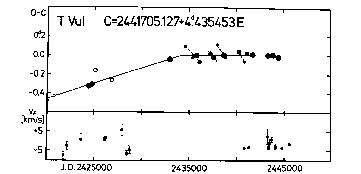
Figure 64. Upper panel: O-C diagram of T Vul
Lower panel: gamma-velocities for the same Cepheid
Table 100. O-C residuals for T Vul
Norm.max. E O-C W Reference
JD2400000+
20001.972 -4893 -0.483 Hertzsprung (1919)
20747.181 -4725 -0.431 Hertzsprung (1919)
24375.483 -3907 -0.329 Huffer (1928a)
24721.463 -3829 -0.314 Huffer (1928a)
25116.367 -3740 -0.166 Hellerich (1935)
26859.398 -3347 -0.268 Kox (1935)
32967.242 -1970 -0.043 Eggen (1951)
34595.189 -1603 0.093 1 Szabados (1977)
35362.401 -1430 -0.028 1 Walraven et al. (1958)
35757.181 -1341 -0.004 3 Prokof'yeva (1961)
36098.640 -1264 -0.074 2 Svolopoulos (1960)
37212.028 -1013 0.015 2 Mitchell et al. (1964)
37562.390 -934 -0.024 3 Johansen (1971)
37939.534 -849 0.107 1 Williams (1966)
38649.098 -689 -0.002 3 Johansen (1971)
38733.365 -670 -0.008 2 Wisniewski & Johnson (1968)
40254.769* -327 0.035 2 Feltz & McNamara (1980)
40853.449* -192 -0.071 1 Evans (1976)
41128.537* -130 0.019 2 Feltz & McNamara (1980)
41705.136 0 0.009 3 Szabados (1977)
43359.552* 373 0.001 3 Moffett & Barnes (1984)
43874.070* 489 0.006 3 Moffett & Barnes (1984)
44472.831* 624 -0.019 3 Berdnikov & Bogdanov (1987)
Table 101. gamma-velocities of T Vul
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
16683 2 9.0 3.0 2 Frost (1904)
16699 19 -1.5 1.5 5 Albrecht (1907)
16765 11 -3.8 3.0 2 Albrecht (1907)
17093 18 1.0 1.5 5 Albrecht (1907)
17151 19 -1.4 0.6 24 Albrecht (1907)
17214 3 -3.5 3.0 2 Albrecht (1907)
17438 7 -0.8 0.8 14 Albrecht (1907)
21796 2 -7.5 2.0 2 Abt (1973)
22166 68 -2.5 2.0 2 Abt (1973)
23622 11 0.8 3.0 2 Harper (1934)
26179 10 0.9 0.9 12 Lust-Kulka (1954)
26220 14 1.8 0.8 16 Lust-Kulka (1954)
27995 1 5.8 3.0 1 Young (1939)
28450 1 -6.4 1.4 3 Abt (1973)
28760 32 -4.5 2.1 3 Young (1939)
40825 24 -3.2 0.3 4 Evans (1976)
41336 11 -2.8 0.4 3 Evans (1976)
43293 1 2.8 4.0 2 Wilson et al. (1989)
43327 33 -2.4 0.3 3 Evans & Lyons (1986)
43377 46 -3.2 0.4 5 Beavers & Eitter (1986)
43382 4 -3.2 0.9 21 Wilson et al. (1989)
43500 5 -0.7 2.0 5 Wilson et al. (1989)
43735 69 1.1 1.2 11 Barnes et al. (1987)
44134 81 -2.2 1.1 12 Barnes et al. (1987)
44136 36 -2.8 0.2 4 Evans & Lyons (1986)
44811 1 -3.2 0.4 1 Evans & Lyons (1986)
45539 24 -1.6 0.2 4 Evans & Lyons (1986)
Before J.D. 2434500 the pulsation period was somewhat longer (see Figure
64): P = 4.435589 days, as determined in Paper I. Moreover, it cannot be
excluded that the period of pulsation before J.D. 2419000 practically
coincided with the recent value, i.e. a phase slide occurred between J.D.
2419000 and 2434500. This phenomenon cannot be followed in Figure 64,
because the early visual observations have not been analysed here. Another
kind of phase jump can, however, be suspected in the recent part of the
O-C graph. In Figure 64 dashed lines indicate these assumed phase jumps.
The quasi-period in the recurrence of these jumps is the same as the value
of the orbital period of T Vul discussed below. This phenomenon is similar
to that observed in Y Oph (see Paper IV, p. 39).
The variation in the gamma-velocity exceeds the limit that could be
attributed to the observational uncertainty. The considerably large number
of the gamma-velocities listed in Table 101 (and partly plotted in the lower
panel of Figure 64) has been analysed for the possible periodicity. A
reasonably good "orbital" radial velocity curve could be obtained at a
period of 1745 days. This phase diagram is plotted in Figure 65. The only
strongly deviating gamma-velocity is the point determined from Frost's (1904)
two radial velocity measurements, being the earliest velocity data for
T Vul. Interestingly enough, Kovacs et al. (1990) also found a long
periodicity in the radial velocity data (their sample was a subset of the
data studied here), but the period of 738 days discovered by them cannot be
revealed from the present sample. The strong coincidence of the 1745 day
period with the cycle length of the subtle phase jumps in the O-C diagram
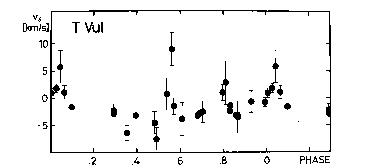
Figure 65. gamma-velocity values of T Vul folded with the 1745 day period
confirm the author's belief that this longer period represents the orbital
period of the binary system containing T Vul. The presence of a companion
star has already been suspected by Kurochkin (1966).
Extensive photometric and spectroscopic observations would be necessary
to obtain a more reliable picture on the duplicity of T Vul.
U Vulpeculae
The O-C diagram covering almost a century was approximated with a
single straight line in Paper II. The photoelectric O-C residuals
supplemented with some more data published in the eighties (see Table 102
and Figure 66) are better represented by two linear sections. It has to be
noted that the extrapolation of this alternating period change towards the
earlier visual observations also gives a reasonably good fit to the O-C
residuals. The O-C residuals listed in Table 102 have been obtained with
the elements:
C = 2442526.312+ 7.990821d*E (75)
+-.006 +-.000026
The gamma-velocities of U Vul show an intrinsic variation (see Table 103
and the lower panel of Figure 66) which can be explained with the
duplicity of U Vul. The existence of a companion was already suspected by
Kurochkin (1966). The gamma-velocities derived from Sanford's (1928) radial
velocity data indicate that the orbital period might not be too long (i.e.
much longer than 1000 days). The formal period search routine applied to
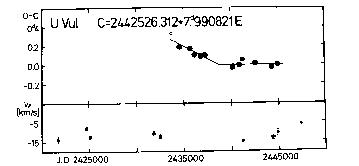
Figure 66. Upper panel: O-C diagram of U Vul
Lower panel: gamma-velocities for the same Cepheid
Table 102. O-C residuals for U Vul
Norm.max. E O-C W Reference
JD2400000+
33704.781 -1104 0.335 1 Chuprina (1952)
34591.618 -993 0.191 3 Szabados (1980)
35638.397 -862 0.173 3 Walraven et al. (1958)
36125.772 -801 0.108 3 Bahner & Mavridis (1971)
36781.008 -719 0.096 3 Weaver'et al. (1960)
37244.483 -661 0.104 3 Mitchell et al. (1964)
40121.046 -301 -0.029 3 Asteriadis et al. (1977)
40208.971* -290 -0.003 1 Feltz & McNamara (1980)
40840.247 -211 -0.002 3 Evans (1976)
41199.889* -166 0.053 2 Feltz & McNamara (1980)
42526.328 0 0.016 3 Szabados (1980)
44292.262* 221 -0.021 3 Moffett & Barnes (1984)
44923.562* 300 0.004 3 Moffett & Barnes (1984)
Table 103. gamma-velocities of U Vul
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
21759 28 -13.5 1.7 4 Sanford (1928)
24745 39 -7.9 0.9 13 Sanford (1928)
25111 48 -12.5 0.9 13 Sanford (1928)
31776 185 -10.5 1.2 7 Sanford (1951)
32494 128 -12.1 1.2 7 Sanford (1951)
41067 116 -14.7 0.3 6 Evans (1976)
44369 219 -13.0 1.1 15 Barnes et al. (1988)
44877 76 -10.5 1.6 7 Barnes et al. (1988)
47365 1 -6.1 0.4 1 Samus (1990)
the gamma-velocity values of U Vul resulted in the orbital period of 868
days. This value, however, cannot be accepted without reservation. The
determination of the true value of the orbital period is not possible
without performing new radial velocity measurements. Photometric
observations would be necessary, as well, in order to study whether the
alternating period changes represent a kind of phase jump (or phase slide)
characteristic of binary Cepheids. It is clear, however, that the
alternating period changes cannot be replaced with a sinusoidal wave
caused by the light-time effect, because the gamma-velocity data indicate
an oscillation in the O-C diagram that would hardly be detected.
X Vulpeculae
The O-C residuals of X Vul listed in Table 104 have been obtained
using the ephemeris:
C = 2442665.932 + 6.319490d*E (76)
+-.012 +-.000022
Instead of a single straight line, the O-C plot has been approximated with
two sections and a phase jump in between (see Figure 67). This phase jump,
however, has to be confirmed.
The gamma-velocity of X Vul varies, and this Cepheid probably belongs to a
long period spectroscopic binary (see Table 105 and the lower panel of
Figure 67). Moffett and Barnes (1987) also noted the discrepancy between
the gamma-velocity values determined at two epochs, while Janot-Pacheco
(1976) suspected a photometric companion.
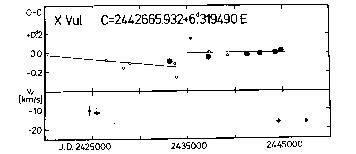
Figure 67. Upper panel: O-C diagram of X Vul
Lower panel: gamma-velocities for the same Cepheid
Table 104. O-C residuals for X Vul
Norm.max. E O-C W Reference
JD2400000+
17470.166 -3987 0.041 1 Luizet (1907)
26481.643 -2561 -0.075 1 Kukarkin (1940)
28314.212 -2271 -0.158 1 Azhusenis (1956)
28984.128 -2165 -0.108 1 Azhusenis (1956)
33117.093 -1511 -0.090 3 Eggen (1951)
33692.141 -1420 -0.115 1 Chuprina (1954b)
33868.946 -1392 -0.256 1 Chuprina (1954b)
35354.434 -1157 0.152 1 Walraven et al. (1958)
37205..847 -864 -0.046 3 Mitchell et al. (1964)
37357.564 -840 0.004 1 Boyko (1970)
39291.295 -534 -0.029 1 Boyko (1970)
41294.584* -217 -0.019 3 Feltz & McNamara (1980)
42665.923 0 -0.009 3 Szabados (1980)
44296.367* 258 0.007 3 Moffett & Barnes (1984)
44909.375* 355 0.024 3 Moffett & Barnes (1984)
Table 105. gamma-velocities of X Vul
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
24748 2 -10.1 2.6 4 Joy (1937)
25490 233 -11.2 2.6 4 Joy (1937)
44504 273 -16.2 1.4 9 Barnes et al. (1988)
47361 1 -16.2 0.8 1 Samus (1990)
SV Vulpeculae
SV Vul is a very important Cepheid because of several reasons. Not
only is SV Vul one of the longest period Cepheids in our Galaxy, but it is
a possible member of the Vul OB1 association (see Walker, 1987 and the
references therein).
Table 106. O-C residuals for SV Vul
Norm.max. E O-C W Reference
JD2400000+
23244.975 -454 -38.321 1 Kristensen (1923,1924)
23470.600 -449 -37.730 1 Leiner (1924)
23651.731 -445 -36.626 1 Zakharov (1924a,1924b)
23877.517 -440 -35.874 1 Kristensen (1926)
23923.562 -439 -34.836 1 Beyer (1930)
23967.607 -438 -35.798 1 Ahnert (1931)
24013.407 -437 -35.004 1 Zakharov (1928)
24148.197 -434 -35.235 1 Leiner (1929)
24329.463 -430 -33.996 1 Zakharov (1928)
24374.633 -429 -33.833 1 Beyer (1930)
24419.533 -428 -33.940 1 Nielsen (1927b)
24511.449 -426 -32.037 1 Ahnert (1931)
24736.039 -421 -32.481 1 Leiner (1929)
24736.624 -421 -31.896 1 Beyer (1930)
24781.299 -420 -31.228 1 Zakharov (1928)
25142.885 -412 -30.696 1 Beyer (1930)
25143.425 -412 -30.156 1 Ahnert (1931)
25369.366 -407 -29.249 1 Leiner (1929)
25550.091 -403 -28.552 1 Beyer (1930)
25865.787 -396 -27.903 1 Ahnert (1931)
25866.102 -396 -27.588 1 Kukarkin (1940)
25955.541 -394 -28.163 1 Zakharov (1954)
26180.987 -389 -27.751 1 Ahnert (1931)
26406.522 -384 -27.250 1 Zverev (1936)
26453.088 -383 -25.691 1 Terkan (1935)
26677.903 -378 -25.910 1 Kukarkin (1940)
26904.924 -373 -23.923 1 Florya & Kukarkina (1953)
27265.565 -365 -23.336 1 Florya & Kukarkina (1953)
28077.230 -347 -21.793 1 Nassau & Ashbrook (1942)
28754.097 -332 -20.028 1 Dziewulski & Iwanowska (1946)
32948.126 -239 -11.632 3 Eggen (1951)
33535.518 -226 -9.328 1 Chuprina (1953)
35340.791 -186 -4.327 1 Walraven et al. (1958)
37232.711 -144 -2.693 3 Mitchell et al. (1964)
37952.866 -128 -2.647 1 Williams (1966)
38268.336 -121 -2.224 3 Fernie et al. (1965)
40654.719* -68 -1.202 2 Feltz & McNamara (1980)
41329.910* -53 -1.113 2 Feltz & McNamara (1980)
43085.550 -14 -0.738 3 Fernie (1979a)
43625.769* -2 -0.600 3 Moffett & Barnes (1984)
43715.229 0 -1.154 3 Szabados (1981)
44075.401* 8 -1.036 3 Moffett & Barnes (1984)
44480.354* 17 -1.145 1 present paper
44525.619* 18 -0.886 2 Eggen (1983b)
45652.558* 43 0.883 3 Berdnikov (1986)
46283.295* 57 1.524 3 Berdnikov (1987)
The behaviour of the period changes of this classical Cepheid
continues to be very interesting. As it was pointed out in Paper III,
erratic changes appear superimposed on the general parabolic trend of the
O-C diagram. The new O-C residuals, as well as the earlier ones (corrected
according to the new normal light curve) are listed in Table 106. The plot
of these residuals shown in Figure 68 has been obtained with the elements:
C = 2443716.383 + 45.0068d*E (77)
+-.181 +-.0026
The parabolic fit, also shown in Figure 68 corresponds to the continuous
period decrease:
P = 45.0068d - 3.64d*10^-4*E (78)
+-.0026 +-.12
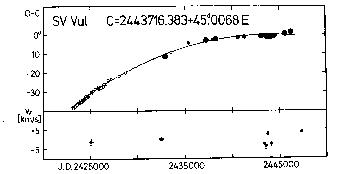
Figure 68. Upper panel: O-C diagram of SV Vul
Lower panel: gamma-velocities for the same Cepheid
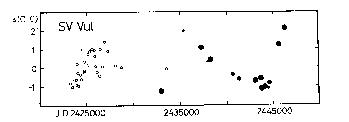
Figure 69. Delta(O-C) diagram of SV Vul
Table 107. gamma-velocities of SV Vul
J.D. sigma v gamma sigma n Reference
2400000+ [d] [km/s] [km/s]
25121 249 -1.2 1.4 11 Joy (1937)
32503 181 0.4 0.8 15 Sanford (1956)
43336 63 -2.4 0.3 5 Fernie (1979a)
43502 5 -3.6 1.6 7 Wilson et al. (1989)
43709 75 2.7 1.0 15 Barnes et al. (1987)
44110 67 -2.5 1.2 11 Barnes et al. (1987)
47311 1 4.0 0.6 2 Samus (1990)
The deviation of the individual O-C residuals from this parabola, i.e. the
Delta (O-C) diagram is shown in Figure 69. Figures 68 and 69 clearly indicate
the commencement of a new positive deviation in the mid-eighties. The
oscillation about the parabola seems to be cyclic with a cycle-length of
slightly longer than ten thousand days (see also Schroder, 1978). The
amplitude of this oscillation is considerable: it reaches 0.03 pulsation
phase, and by no means is caused by the light-time effect. Since the recent
deviation has not been taken into account in calculating the forthcoming
maxima, the numerical data for SV Vul in Table 110 may be in error. Regular
photometric study of SV Vul is desirable.
The gamma-velocity values determined for SV Vul are collected in Table
107. Although the extreme values differ from each other by more than 7
km/s, the variability in the gamma-velocity cannot be stated, because the
extreme values have been determined from radial velocity data, either of
poor quality or small in number.
GENERAL REMARKS
A considerable fraction of the Cepheids in this sample has been known
to exhibit characteristic period changes. In order to achieve a more
complete coverage in the O-C diagram, selected programme stars have been
observed with the 50 cm Cassegrain telescope at Piszkesteto Mountain
Station of Konkoly Observatory. This telescope is equipped with an
integrating photoelectric photometer (containing an EMI 9058QB type
multiplier) and standard UBV filters. The individual observational data are
listed in Table 108. The mean error of these new photometric measurements
is about 0.01 in V and B, and somewhat larger in U. The observations have
been transformed into the standard UBV system, but the data on V636 Cas are
only differential magnitudes with respect to the comparison star BD +62 259.
Table 108. New photoelectric observations of selected Cepheids
J.D.Hel. V B-V U-B J.D.Hel. V B-V U-B
2440000+ 2440000+
FF Aql (BY Cas)
3287.491 5.45 0.79
3304.438 5.56 0.78 4162.493 10.24 1.19
3337.388 5.29 0.69 4166.325 10.43 1.28
3382.375 5.22 0.68 4167.490 10.61 1.30
3385.336 5.51 0.83 4203.302 10.54 1.19
3386.312 5.36 0.74 4251.285 10.62 1.30
3388.350 5.41 0.78
3401.363 5.33 0.73 J.D.Hel. V B-V U-B
3438.255 5.50 0.81 2440000+
3599.595 5.52 0.84 DD Cas
3647.441 5.39 0.75 4874.397 10.26: 1.35:
3737.333 5.44 0.80 4972.244 10.09 1.34
3739.338 5.39 0.74 5229.432 10.25 1.30
3743.424 5.47 0.80 5259.352 10.15 1.30
3765.345 5.51 0.82 5294.352 9.91 1.21
3772.280 5.32 0.71
3789.305 5.20 0.65 J.D.Hel. Delta V Delta(B-V)
3800.218 5.49 0.80 2440000+
6597.372 5.23 0.66 0.46 V636 Cas
6612.424 5.50 0.80 0.47 5200.515 -0.322 0.832
6614.374 5.36 0.72 0.50 5229.408 -0.293 0.800
6652.382 5.45 0.79 0.64 5259.464 -0.311 0.823
6653.339 5.54 0.80 0.52 7791.437 -0.294 0.896
J.D.Hel. V B-V U-B J.D.Hel. V B-V U-B
2440000+ 2440000+
RW Cam IR Cep
6466.268 8.32 1.21 0.90 7316.500 7.80 0.82 0.48
6467.275 8.16 1.19 0.95 7387.529 7.65 0.75 0.51
6489.364 8.67 1.48 1.02 7388.462 7.85 0.86 0.55
6490.360 8.76 1.49 0.93 7438.233 7.65: 0.71: 0.46:
7174.467 8.28 1.29 0.95 7438.385 7.62 0.73 0.52
7175.473 8.35 1.39 0.98 7439.360 7.90 0.88 0.56
7443.581 8.84 1.51 0.92 7439.439 7.91 0.89 0.53
7444.530 8.93 1.49 0.87 7440.268 7.71 0.78 0.49
7441.236 7.82 0.84 0.55
J.D.Hel. V B-V U-B
2440000+ J.D.Hel. V B-V U-B
BY Cas 2440000+
3382.524 10.13 1.23 SU Cyg
3420.472 10.36 1.21 3304.451 7.15 0.69
3425.456 10.48 1.36 3337.375 6.73 0.58
3426.433 10.48 1.33 3351.527 6.65 0.49
3437.474 10.23 1.12 3363.513 6.45 0.42
3489.328 10.26 1.30 3375.464 6.66 0.48
3490.319 10.59 1.37 3388.415 7.03 0.68
3572.247 10.24 1.25 3401.387 6.84 0.54
4108.530 10.51: 1.20: 3403.325 6.98 0.65
4143.422 10.29 1.21 3424.256 7.05 0.61
4157.406 10.62 1.31 3440.234 6.46 0.41
4159.392 10.37 1.10 4372.461 7.01 0.63
Table 108. (cont.)
J.D.Hel. V B-V U-B J.D.Hel. V B-V U-B
2440000+ 2440000+
(SU Cyg) (DT Cyg)
4402.459 6.73 0.55 4159.271 5.66 0.42
4455.393 6.45 0.41 4166.277 5.80 0.50
4458.535 7.16 0.63 4215.191 5.83 0.50
4811.391 7.15 0.67 4458.423 5.92 0.51
4822.436 7.01 0.63 4486.328 5.76 0.44
4840.386 6.54 0.46 4811.473 5.71 0.42
4862.346 7.18 0.61 4822.468 5.86 0.51
4870.303 6.96 0.58 4840.417 5.93 0.55
4874.308 6.75 0.51
5200.451 7.19 0.70 J.D.Hel. V B-V U-B
5224.376 6.59 0.44 2440000+
5229.331 6.76 0.55 V532 Cyg
5259.286 6.46 0.40 3353.552 9.23 1.14
5294.273 6.58 0.47 3375.562 9.08 1.12
6222.490 7.06 0.70 0.46 3382.460 9.18 1.14
6266.455 6.70 0.52 0.44 3388.498 9.05 1.09
6268.445 7.02 0.69 0.45 3401.451 8.96 1.06
6271.433 6.74 0.56 0.45 3403.349 9.11 1.08
6387.241 6.90 0.64 0.45 3437.297 8.92 0.99
6597.429 6.46 0.40 0.47 3440.262 8.94 0.99
6652.413 6.84 0.63 0.49 3476.218 8.88 1.01
6653.372 7.11 0.70 0.48 3481.227 9.25 1.14
7791.361 7.05 0.69 0.43 3489.218 8.97 1.02
7792.321 7.19 0.71 0.44 4108.486 9.30 1.19
4111.589 9.23 1.18
J.D.Hel. V B-V U-B 4113.401 8.91 1.06
2440000+ 4157.350 9.15 1.15
DT Cyg 4162.418 9.02 1.07
3351.538 5.83 0.48 4166.338 8.94 1.06
3363.538 5.92 0.55 4173.267 9.05 1.10
3375.426 5.82 0.49 4203.267 9.30: 1.05:
3382.359 5.68 0.45 4811.503 9.25 1.15
3382.477 5.70 0.44 4822.498 8.90 1.05
3386.349 5.90 0.53 4840.439 9.23 1.14
3388.452 5.93 0.55 4862.391 9.02 1.07
3403.312 5.94 0.56 4870.347 9.27 1.17
3437.229 5.69 0.44 4874.347 9.14 1.16
3440.248 5.75 0.49 5224.403 9.19 1.19
3489.228 5.74 0.46 5229.359 8.94 1.08
3714.543 5.72 0.38 5259.316 8.93 1.06
3722.566 5.78 0.47 5294.318 9.22 1.12
3736.444 5.83 0.49 6268.511 9.14 1.12
3743.463 5.90 0.54 6387.309 9.26 1.15
3765.357 5.86 0.54 6652.496 9.10 1.13
3772.433 5.73 0.47 6653.475 9.24 1.17
3789.372 5.63 0.44 7388.421 9.20 1.15
3798.260 5.98 0.54 7438.346 9.25 1.14
4108.449 5.91 0.52 7439.405 8.93 1.01
4111.473 5.73 0.47 7443.435 8.99 1.04
4129.387 5.67 0.42 7444.328 9.21 1.17
4157.326 5.75 0.47 7791.339 8.94 1.04
7792.353 9.20 1.17
Table 108. (cont.)
J.D.Hel. V B-V U-B J.D.Hel. V B-V U-B
2440000+ 2440000+
TX Del AW Per
4458.468 8.98 0.62 4633.429 7.86 1.22
4462.399 9.33 0.82 4637.427 7.42 1.14
4661.337 7.07 0.93
J.D.Hel: V B-V U-B 6466.321 7.41 1.09 0.73
2440000+ 6467.326 7.56 1.15 0.75
Y Lac 6489.403 7.63 1.09 0.68
4458.516 8.99 0.68 6490.400 7.06 0.89 0.68
7174.389 7.73 1.13 0.71
J.D.Hel. V B-V U-B 7175.407 7.06 0.87 0.71
2440000+ 7443.568 7.64 1.18 0.79
CV Mon 7444.574 7.80 1.21 0.78
6466.360 10.54 1.46
6467.353 10.45 1.37 J.D.Hel. V B-V U-B
2440000+
J.D.Hel. V B-V U-B S Sge
2440000+ 4811.440 5.65 0.86
RS Ori 6597.447 5.74 0.93 0.78
4633.470 8.69 1.14 6614.423 5.82 0.91 0.84
4637.453 8.11 0.87 6652.399 5.32 0.61 0.53
4661.392 8.23 0.96 6653.356 5.38 0.69 0.53
6691.254 5.98 0.98 0.83
J.D.Hel. V B-V U-B
2440000+ J.D.Hel. V B-V U-B
SV Per 2440000+
4633.448 8.99 1.19 SZ Tau
4661.358 9.04 1.02 4633.409 6.66 0.90
4661.261 6.52 0.84
J.D.Hel. V B-V U-B
2440000+ J.D.Hel. V B-V U-B
VX Per 2440000+
4638.304 9.07 1.18 S Vul
4661.299 9.11 1.13 4811.458 9.44 1.73
4822.451 9.14 1.56
J.D.Hel. V B-V U-B 4840.400 8.96 1.57
2440000+ 4870.318 9.31 1.83
AS Per 4874.327 9.40 1.77
3385.570 9.33 1.45
3420.592 9.47 1.44 J.D.Hel. V B-V U-B
3423.588 9.93 1.61 2440000+
3424.576 9.12 1.28 SV Vul
3437.460 9.85 1.67 4455.426 7.32 1.70
3458.651 9.70 1.56 4458.550 7.41 1.72
3481.315 9.72 1.56
3490.492 9.49 1.52
3546.247 9.79 1.55
3560.415 9.54 1.58
3572.261 9.98 1.72
3598.293 9.28 1.36
Table 109. New radial velocity measurements of selected Cepheids
Cepheid J.D.Hel. radial sigma number of dispersion
2440000+ velocity (km/s) lines (A/mm)
FF Aql 6727.269 -23.8 km/s 1.6 17 9
DT Cyg 5270.297 1.9 2.3 17 9
AW Per 6726.512 9.7 3.9 21 18
AW Per 6727.498 19.7 2.9 18 18
S Sge 6726.281 -12.9 2.4 22 9
Several spectrograms of binary Cepheids were also taken with the coudee
spectrograph attached to the 2m telescope of Rozhen Observatory
(Bulgaria). The spectra were obtained at a dispersion of either 9 A/mm or
18 A/mm at H gamma. The individual radial velocity values are listed in Table
109.
A brief summary on the period, period changes and gamma-velocity
variations is compiled in Table 110. The subsequent columns of this table
contain the following data:
1. Name of the Cepheid,
2. Moment of the normal maximum just following J.D. 2450000,
3. Pulsation period expected at J.D. 2450000. This value is calculated with
the help of the corresponding (linear or parabolic) ephemeris published
in the previous discussion on the given star,
4. Characteristic features in the O-C diagram,
5. Variability in the gamma-velocity,
6. Value of the orbital period,
7. Reference to the paper where the value cited in the previous column has
been published.
The use of J.D. 2450000 seems to be a reasonable compromise, because the
extrapolation of the current elements for 1995 is not hazardous in the
overwhelming majority of the cases. There are only eight stars (V572 Aql,
BY Cas, DT Cyg, DX Gem, T Mon, VX Per, V440 Per, and SV Vul) in this
sample, exhibiting either a quite recent period change or a deviation from
the parabolic fit, that may cause some uncertainty in the prediction of the
ephemeris.
The extension of the O-C diagrams to a larger time-base and the use of
more accurate observations resulted in a different from the previous
interpretation of the period changes in a number of cases. Instead of a
single sudden period change (i.e. two linear sections in the O-C diagram) a
continuous change in the period (i.e. parabolic O-C graph) is suggested for
VZ Cyg, W Gem, RZ Gem, RR Lac, S Sge, and SW Tau.
The phase jump interpretation proposed in Papers I-III has been
confirmed in most cases, and in addition, this phenomenon seems to have
happened to some more Cepheids. The list of the northern Cepheids showing a
phase jump in their pulsation is as follows: FF Aql, BY Cas, DD Cas,
DL Cas, X Cyg, SU Cyg, SZ Cyg, DT Cyg, V532 Cyg, V924 Cyg, TX Del, DX Gem,
X Lac, CV Mon, RS Ori, SV Per, SZ Tau, T Vul, X Vul. The phase jump appears
most clearly in the case of FF Aql and SU Cyg, while its occurrence has to
be confirmed in the case of some stars listed above (see Table 110). For
FF Aql the phase shift has also been detected in the radial velocity data
(Evans et al. 1990b). SU Cyg is unique in the respect that the phase jump
was accompanied with a noticeable change in the shape of the light curve.
The phenomenon of the phase shift is a feature occurring in binary
Cepheids, and its repeated occurrence in the same star (Y Oph in Paper IV,
TX Del and T Vul in this paper) suggests that the jump is triggered by the
orbital motion.
The orbital motion itself can be followed in the O-C diagram via the
light-time effect. This phenomenon is best seen in AW Per, but may also be
present in the O-C plot of FM Aql, RW Cam, Y Lac, and RS Ori. This latter
Cepheid is especially important because RS Ori might be the first case of
exhibiting a phase jump and the light-time effect in the same O-C diagram.
The alternating period changes on a time-scale of several years or
decades can be attributed to solar type activity cycles (Hall, 1990). The
present sample contains several Cepheids showing quasi-cyclic changes in
the pulsation period, viz. Zeta Gem, T Mon, S Vul, and SV Vul. Although the
number of Cepheids forming this group is small, it may be significant
that the shortest pulsation period for a member is longer than 10 days. A
problem to be solved in the future is the differentiation between the phase
slip (a slower or more gradual phase jump) and the alternate period changes
due to magnetic effects. The solar type activity cycle does not necessitate
the duplicity of the star involved, although a companion star usually
strengthens the activity.
The analysis of the radial velocity observations has resulted in
revealing a number of new spectroscopic binary Cepheids or candidates.
The most promising cases are: KL Aql, Eta Aql, SU Cas, V636 Cas, BZ Cyg,
MW Cyg, V386 Cyg, W Gem, RZ Gem, AD Gem, RS Ori, SV Per, SW Tau, T Vul,
U Vul. An attempt was made to find the value of the orbital period for
Cepheids with ample radial velocity data, but each spectroscopic period
derived here has to be confirmed with the help of additional measurements.
Table 110. Summary on the periods, period changes and duplicity
Cepheid Norm.max. Period O-C graph v gamma P orb Source
2400000+ [d]
SZ Aql 50012.262 17.141745 parabolic (+) ?
TT Aql 50000.687 13.754954 linear var.?
FF Aql 50004.063 4.470936 lin. with PHJ var. 1430 Evans et al. (1990)
FM Aql 50003.142 6.114265 linear (+LTE?) const.? 2800 ? this paper
KL Aql 50002.539 6.108015 linear var. short this paper
V572 Aql 50000.287 3.768001 linear (?) -
V1344 Aql 50000.187 7.476787 linear var.?
Eta Aql 50000.175 7.176758 parabolic (+) var. 926 ? this paper
RT Aur 50000.279 3.728198 linear const.
AN Aur 50003.628 10.289563 linear var.
RW Cam 50012.740 16.415015 lin. with LTE or PHJ var. 7000 ? this paper
SU Cas 50000.720 1.949325 linear var. 462.5 ? this paper
SZ Cas 50009.120 13.645356 parabolic (+) var.?
BY Cas 50000.908 3.222199 lin. with PHJ ?
DD Cas 50001.805 9.811656 lin.(+ PHJ?) var.?
DL Cas 50004.712 8.000598 lin. with PHJ var. 688.0 Harris et al. (1987)
IX Cas 50003.203 9.154549 irregular var. 110.29 Harris and Welch (1989)
V636 Cas 50005.366 8.375735 linear var.
IR Cep 50000.719 2.114088 linear (+EPCH) one
V351 Cep 50000.179 2.806052 linear (+EPCH) -
X Cyg 50007.657 16.385692 lin. with PHJ var.?
SU Cyg 50000.682 3.845512 lin. with PHJ var. 549.16 Evans (1988)
SZ Cyg 50000.868 15.110228 lin. with PHJ var.
TX Cyg 50003.317 14.711635 linear (+EPCH) var.?
VZ Cyg 50004.454 4.864372 parabolic (-) var.?
BZ Cyg 50001.523 10.142222 linear var.
DT Cyg 50002.270 2.499086 lin. with PHJ var.
MW Cyg 50004.005 5.954666 linear var.
V386 Cyg 50001.131 5.257635 linear var.
V532 Cyg 50000.792 3.283494 lin. with PHJ var.?
V924 Cyg 50002.268 5.571305 lin. with PHJ -
V1334 Cyg 50002.920 3.332804 linear var. <1240 this paper
V1726 Cyg 50003.570 4.236978 one
TX Del 50000.932 6.165904 lin.(+ PHJ?) var. 133.15 Harris and Welch (1989)
Table 110. (cont.)
Norm.max. Period O-C graph v gamma P orb Source
Cepheid 2400000+ [d] [d]
W Gem 50003.897 7.913277 parabolic (-) var.
RZ Gem 50002.248 5.528942 parabolic (-) var. 886? this paper
AD Gem 50002.061 3.787990 linear var.
DX Gem 50001.290 3.136779 lin. with PHJ var.? Burki (1985)
Zeta Gem 50007.231 10.149414 parabolic (-) var.?
V Lac 50000.245 4.983002 parabolic (-) var.?
X Lac 50000.890 5.444322 lin. with PHJ var.?
Y Lac 50000.797 4.323769 linear var.?
Z Lac 50000.760 10.885600 parabolic (-) var. short this paper
RR Lac 50001.448 6.416335 parabolic (+) var.
BG Lac 50004.552 5.331902 linear var.?
T Mon 50025.601 27.020097 lin.On par.(+) var. very long Gieren (1989b)
SV Mon 50009.142 15.232582 linear const.
CV Mon 50002.177 5.378804 lin. with PHJ one
V465 Mon 50000.505 2.713006 linear (+EPCH) var. Burki (1985)
RS Ori 50001.701 7.566841 lin. with LTE and PHJ var. long ? this paper
GQ Ori 50001.590 8.616283 linear one
SV Per 50004.946 11.129319 lin.(+ PHJ?) var.
VX Per 50008.306 10.886972 linear (+EPCH) const.
AS Per 50003.220 4.972540 linear one
AW Per 50000.041 6.463622 lin. with LTE var. 13100 Welch and Evans (1989)
V440 Per 50003.336 7.572498 linear (?) const.
S Sge 50004.834 8.382184 parabolic (+) var. 676.2 Slovak and Barnes (1987)
SW Tau 50001.443 1.583540 parabolic (-) var.
SZ Tau 50001.329 3.149138 lin. with PHJ var.?
S Vul 50038.692 68.500 lin. sections ?
T Vul 50003.860 4.435453 lin. with PHJ var. 1745 this paper
U Vul 50005.698 7.990821 linear (+EPCH) var. 868 ? thiis paper
X Vul 50002.860 6.319490 lin.(+ PHJ?) var.
SV Vul 50013.768 44.9558 parabolic (-) const.?
Legend: LTE : light-time effect (+) and (-) : continuous period increase or decrease
PHJ : phase jump(s) ? : poorly covered radial velocity curve,
EPCH : earlier period change(s) the gamma-velocity cannot be determined
one : only one series of radial velocity data - : radial velocity observations have not been made
A new method, independent from the previously used ones, has been
proposed for revealing the presence of a companion. This evidence is based
on the amplitude ratio of the light and radial velocity variability (see
V440 Per).
The new discoveries and uncertainties confirm the fact that there is a
huge number of Cepheid variables deserving regular attention (photometric
and radial velocity studies), and/or occasional close inspection in the
form of a detailed spectroscopic analysis.
The author is grateful to Drs. M. Kun and B. Szeidl for their useful
comments and encouragement during accomplishing this project. Thanks are
also due to the staff of Rozhen Observatory (especially to Dr. I. Iliev)
for the help in obtaining and reducing the new radial velocity data listed
in Table 109. Generosity of several colleagues (putting at my disposal
their observational data prior to publication) is also acknowledged: Dr.
N.N. Samus handed me the whole list of his group's radial velocity
results, Dr. G. Wallerstein sent a list of photometric observations on SW
Tau, and Dr. R.F. Griffin informed me about the unpublished radial
velocity data on AW Per. The author's thanks are also extended to Mr. P.
Decsy for preparing the figures.
Budapest - Szabadsaghegy, 6 May 1991
References:
Abidov, Z. 1963, Perem. Zvezdy, 14, 493. (1963PZ.....14..493A)
Abt, B.A. 1959, Astrophys. J., 130, 1021. (1959ApJ...130.1021A)
Abt, B.A. 1970, Astrophys. J. Suppl., 19, 387. (1970ApJS...19..387A)
Abt, B.A. 1973, Astrophys. J. Suppl., 26, 365. (1973ApJS...26..365A)
Abt, B.A. 1978, Pub. Astr. Soc. Pacific, 90, 309. (1978PASP...90..309A)
Abt, H.A. and Levy, S.G. 1970, Pub. Astr. Soc. Pacific, 82, 334. (1970PASP...82..334A)
Abt, H.A. and Levy, S.G. 1974, Astrophys. J., 188, L75. (1974ApJ...188L..75A)
Adams, W.S. and Shapley, H. 1918, Astrophys. J., 47, 46. (1918ApJ....47...46A)
Ahnert, P. 1931, Astr. Nachr., 241, 265. (1931AN....241..265A)
Ahnert, P. 1951, Mitt. veranderl. Sterne, No. 133.
AFOEV 1922, Bull. Obs. Lyon, 4, 189.
AFOEV 1923, Bull. Obs. Lyon, 5, 178.
Albrecht, S. 1907, Astrophys. J., 25, 330. (1907ApJ....25..330A)
Arellano Ferro, A. 1984, Mon. Not. R. astr. Soc., 209, 481. (1984MNRAS.209..481A)
Arellano Ferro, A., Giridhar, S., and Parrao, L. 1987, Inf. Bull. Var. Stars, No., 3077. (IBVS N°.3077)
Arellano Ferro, A. and Madore, B.F. 1986, Astrophys. J., 302, 767. (1986ApJ...302..767A)
Argelander, F.W.A. 1869, Astr. Beob. Sternw. Bonn, 7.
Arp, H.C. 1960, Astrophys. J., 131, 322. (1960ApJ...131..322A)
Arp, H.C., Sandage, A., and Stephens C. 1959, Astrophys. J., 130, 80. (1959ApJ...130...80A)
Ashbrook, J. 1954, Astron. J., 59, 11. (1954AJ.....59...11A)
Asteriadis, G., Mavridis, L.N., and Tsioumis, A. 1977, Contr. Dept. Geod. Astr. Univ. Thessaloniki, No. 15.
Azarnova, T.A. 1957, Perem. Zvezdy, 12, 76. (1957PZ.....12...76A)
Azarnova, T.A. 1960a, Perem. Zvezdy, 13, 67. (1960PZ.....13...67A)
Azarnova, T.A. 1960b, Perem. Zvezdy, 13, 288. (1960PZ.....13..288A)
Azhusenis, A.D. 1956, Perem. Zvezdy, 11, 393. (1956PZ.....11..393A)
Bahner, K., Hiltner, W.A., and Kraft, R.P. 1962, Astrophys. J. Suppl. 6, 319. (1962ApJS....6..319B)
Bahner, K. and Mavridis, L.N. 1971, Contr. Dept. Geod. Astr. Univ. Thessaloniki, No., 3.
Bahner, K. and Mavridis, L.N. 1977, Contr. Dept. Geod. Astr. Univ. Thessaloniki, No. 14.
Balona, L.A. 1981, Observatory, 101, 205. (1981Obs...101..205B)
Barnes, T.G. III, Moffett, T.J and Slovak, M.H. 1987, Astrophys. J. Suppl., 65, 307. (1987ApJS...65..307B)
Barnes, T.G. III, Moffett, T.J., and Slovak, M.H. 1988, Astrophys. J. Suppl., 66, 43. (1988ApJS...66...43B)
Bartkus, R. and Puchinskas, A. 1961 Vilnius Biul., No., 3.
Bartolini, C., Dapergolas, A., and Piccioni, A. 1981, Inf.Bull.Var.Stars, No., 2009. (IBVS N°.2009)
Beavers, W.I. and Eitter, J.J. 1986, Astrophys. J. Suppl., 62, 147. (1986ApJS...62..147B)
Belopolski, A. 1897, Astrophys. J., 6, 393. (1897ApJ.....6..393B)
Bellemin, E. 1922, Bull. Obs. Lyon, 4, No., 7, 93.
Bennett, A.L. 1939, Astrophys. J., 90, 289. (1939ApJ....90..289B)
Bennett, A.L. 1941, Astrophys. J. 93, 52. (1941ApJ....93...52B)
Berdnikov, I.N. 1977, Perem. Zvezdy, Pril. 3, 325.
Berdnikov, L.N. 1986, Perem. Zvezdy, 22, 369. (1986PZ.....22..369B)
Berdnikov, L.N. 1987, Perem. Zvezdy, 22, 530. (1987PZ.....22..530B)
Berdnikov, L.N. and Bogdanov, M.B. 1987, Perem. Zvezdy, 22, 549. (1987PZ.....22..549B)
Berdnikov, L.N. and Ivanov, G.R. 1986, Inf. Bull. Var. Stars No., 2856. (IBVS N°.2856)
Bernheimer, W.E. 1931, Medd. Lund. astr. Obs., Ser. II, No., 61.
Beyer, M. 1930, Erg. A.N. 8, No., 3.
Borzdyko, V.I. 1965, Byull. Inst. Astrofiz. Dushanbe, No., 41-42, 55.
Bottlinger, K.F. 1928, Nachr., 232, 3.
Boulon, J., Duflot, M., and Fehrenbach, C. 1958, Publ. Obs. Haute Provence, 4, No., 34.
Boyko, O.S. 1970, Lvov Cirk., No., 44.
Bohm-Vitense, E. and Proffitt, C. 1985, Astrophys. J., 296 ,175. (1985ApJ...296..175B)
Burki, G. 1985, in: "Cepheids: Theory and Observations", Proc. IAU Coll. No., 82, ed. B.F. Madore, Carobridge Univ. Press, Cambridge, p. 34.
Burki, G. and Benz, W. 1982, Astron. Astrophys., 115, 30. (1982A&A...115...30B)
Campbell, W.W. 1899, Astrophys. J., 9, 86. (1899ApJ.....9...86C)
"Carlsberg" 1989, Carlsberg Meridian Catalogue, La Palma, No., 4. Copenhagen University Observatory, Royal Greenwich Observatory, Real Instituto y Observatorio de la Armada en San Fernando.
Carrasco, R. 1932, Bol. Obs. Madrid, 1, No. 1, 6.
Chekhanikhina, O.A. 1982, Byull. Inst. Astrofiz. Dushanbe, No., 71, 25.
Chudovicheva, O.N. 1952, Perem. Zvezdy, 9, 133. (1952PZ......9..133C)
Chuprina, R.I. 1952, Perem. Zvezdy, 9, 164. (1952PZ......9..164C)
Chuprina, R.I. 1953, Perem. Zvezdy, 9, 221. (1953PZ......9..221C)
Chuprina, R.I. 1954a, Perem. Zvezdy, 10, 125. (1954PZ.....10..125C)
Chuprina, R.I. 1954b, Perem. Zvezdy, 10, 130. (1954PZ.....10..130C)
Chuprina, R.I. 1956, Perem. Zvezdy, 11, 61. (1956PZ.....11...61C)
Coker, R., Madore, B.F., Mould, J., Oke, J.B., Picard, A., Huchra, J., and Latham, D. 1989, Pub. Astr. Soc. Pacific, 101, 594. (1989PASP..101..594C)
Collmann, W. 1930, Astr. Nachr., 238, 389. (1930AN....238..389C)
Connolly, L.P., Africano, J.L., Klimke, A., Worden, S.P. 1982, Pub. Astr. Soc. Pacific, 94, 182. (1982PASP...94..182C)
Connolly, L.P., Palmer, L.H., Goodrich, B.D., Halbedel, W., Africano, J.L., and Henry, G.W. 1983, Pub. Astr. Soc. Pacific, 95, 192. (1983PASP...95..192C)
Coulson, I.M. 1983, Mon. Not. R. astr. Soc., 203, 925 (1983MNRAS.203..925C)
Coulson, I.M. and Caldwell, J.A.R. 1985, S.A.A.0. Circ., No. 9, 5.
Coulson, I.M., Caldwell, J.A.R., and Gieren, W.P. 1985, Astrophys. J. Suppl., 57, 595. (1985ApJS...57..595C)
Coulson, I.M., Caldwell, J.A.R., and Gieren, W.P. 1986, Astrophys. J., 303, 273. (1986ApJ...303..273C)
Dawson, D.W. 1979, Astrophys. J. Suppl., 41, 97. (1979ApJS...41...97D)
Dean, J.F. 1977, M.N.A.S.S.A., 36, 3.
Dean, J.F. 1981, S.A.A.0. Circ., 1, No., 6, 10.
Dean, J.F., Cousins, A.W.J., Bywater, R.A., and Warren, P.R. 1977, Mem. R. astr. Soc., 83, 69.
Depenchuk, E.A. 1980, Inf. Bull. Var. Stars, No. 1819. (IBVS N°.1819)
Diethelm, R. 1986, Astron. Astrophys. Suppl., 64, 261. (1986A&AS...64..261D)
Diethelm, R. and Tammann, G.A. 1982, Astron. Astrophys. Suppl., 47, 335. (1982A&AS...47..335D)
Dirks, W.H. and Vaucouleurs, G. 1949, Ann. Astrophys., 12, 219.
Doberck, W. 1920, Astron. J., 32, 188. (1920AJ.....32..188D)
Doberck, W. 1924, Astr. Nachr., 222, 275. (1924AN....222..275D)
Duncan, J.C. 1921, Astrophys. J., 53, 95. (1921ApJ....53...95D)
Dziewulski, W. 1948, Bull. astr. Obs. Univ. Copernicus, No., 6, 3.
Dziewulski, W. and Iwanowska, W. 1946, Bull. astr. Obs. Univ. Copernicus, No. 1, 3.
Eaton, H.O. 1920, Pop. Astr., 28, 423, 543.
Eaton, H.O. 1921, Pop. Astr., 29, 53, 120, 173.
Eaton, H.O. 1922, Pop. Astr., 30, 428, 488.
Eggen, O.J. 1951, Astrophys. J., 113, 367. (1951ApJ...113..367E)
Eggen, O.J. 1969, Astrophys. J., 156, 617. (1969ApJ...156..617E)
Eggen, O.J. 1983a, Astron. J., 88, 361. (1983AJ.....88..361E)
Eggen, O.J. 1983b, Astron. J., 88, 998. (1983AJ.....88..998E)
Eggen, O.J. 1985, Astron. J., 90, 1297. (1985AJ.....90.1297E)
Eggen, 0.J., Gascoigne, S.G.B, and Burr, E.J. 1957, Mon. Not. R. astr. Soc., 117, 406. (1957MNRAS.117..406E)
Enebo, S. 1908, Beob. veranderl. Sterne, angestellt auf Dombaas, Kristiania, H. 2.
Enebo, S. 1909, Beob. veranderl. Sterne, angestellt auf Dombaas, Kristiania, H. 3.
Enebo, S. 1911, Beob. veranderl. Sterne, angestellt auf Dombaas, Kristiania, H. 5.
Enebo, S. 1914, Beob. veranderl. Sterne, angestellt auf Dombaas, Kristiania, H. 8.
Erleksova, G.E. 1960, Byull. Inst. Astrofiz. Dushanbe, No. 29, 23.
Erleksova, G.E. 1961, Byull. Inst. Astrofiz. Dushanbe, No. 30, 28.
Erleksova, G.E. 1978, Inf. Bull. Var. Stars, No. 1460. (IBVS N°.1460)
Evans, N.R. 1976, Astrophys. J. Suppl., 32, 399. (1976ApJS...32..399E)
Evans, N.R. 1983, Astrophys. J., 272, 214. (1983ApJ...272..214E)
Evans, N.R. 1984, Astrophys. J., 281, 760. (1984ApJ...281..760E)
Evans, N.R. 1985, in: "Cepheids: Theory and Observations", Proc. IAU Coll. No. 82, ed. B.F. Madore, Cambridge Univ. Press, Cambridge, p. 79.
Evans, N.R. 1988, Astrophys. J., Suppl., 66, 343. (1988ApJS...66..343E)
Evans, N.R. and Bolton, C.T. 1990, Astrophys. J., 356, 630. (1990ApJ...356..630E)
Evans, N.R. and Lyons, R. 1986, Astron. J., 92, 436. (1986AJ.....92..436E)
Evans, N.R., Slovak, M.H., and Welch, D.L. 1989, in: "The Use of Pulsating Stars in the Fundamental Problems of Astronomy", Proc. IAU Coll. No. 111, ed. E.G. Schmidt, Cambridge Univ. Press, Cambridge, p. 260.
Evans, N.R., Szabados, L., and Udalska, J. 1990a, Pub. Astr. Soc. Pacific, 102, 981. (1990PASP..102..981E)
Evans, N.R., Welch, D.L., Scarfe, C.D., and Teays, T.J. 1990b, Astron. J., 99, 1598. (1990AJ.....99.1598E)
Feltz, K.A. Jr. and McNamara, D.H. 1980, Pub. Astr. Soc. Pacific, 92, 609. (1980PASP...92..609F)
Fernie, J.D. 1970, Astron. J., 75, 244. (1970AJ.....75..244F)
Fernie, J.D. 1979a, Astrophys. J., 231, 841. (1979ApJ...231..841F)
Fernie, J.D. 1979b, Pub. Astr. Soc. Pacific, 91, 67. (1979PASP...91...67F)
Fernie, J.D., Demers, S., and Marlborough, J.M. 1965, Astron. J., 70, 482. (1965AJ.....70..482F)
Fernie, J.D. and Garrison, R.F. 1981, Pub. Astr. Soc. Pacific, 93, 330. (1981PASP...93..330F)
Filatov, G.S. 1961, Byull. Inst. Astrofiz. Dushanbe, No., 30, 67
Filin, A.Ya. 1951, Perem. Zvezdy, 8, 165. (1951PZ......8..165F)
Florya, N.F. and Kukarkina, N.P. 1953, Trudy gos. astr. Inst. Sternberga, 23, 3.
Florya N.F. and Parenago, P.P. 1933, Perem Zvezdy, 4, 317. (1933PZ......4..317F)
Fridel, Yu.B. 1971, Lvov Cirk., No., 45, 32.
Frost, E.B. 1904, Astrophys. J., 20, 296. (1904ApJ....20..296F)
Frost, E.B. 1906, Astrophys. J., 23, 264. (1906ApJ....23..264F)
Gallisot, C. 1923, Bull. astr., Ser., 2, 3, 207.
Gesundheit, S.Z. 1938, Wilno Bull., No., 20.
Gieren, W. 1976, Astron. Astrophys., 47, 211. (1976A&A....47..211G)
Gieren, W.P. 1985, Astron. Astrophys. 148, 138. (1985A&A...148..138G)
Gieren, W.P. 1988, Pub. Astr. Soc. Pacific, 100, 262. (1988PASP..100..262G)
Gieren, W.P. 1989a, Pub. Astr. Soc. Pacific, 101, 160. (1989PASP..101..160G)
Gieren, W.P. 1989b, Astron. Astrophys., 216, 135. (1989A&A...216..135G)
Gieren, W.P. and Brieva, E. 1990, in "Confrontation between Stellar Pulsation and Evolution", eds. C. Cacciari and G. Clementini, ASP Conf. Series, 11, p. 222.
Girnyak, M.B. 1964, Lvov Cirk., No., 41, 20.
Girnyak, M.B. 1971, Lvov Cirk., No., 45, 17.
Golovatyj, V.V. 1964, Lvov Cirk., No., 41, 25.
Gore, J.E. 1886, Mon. Not. R. astr. Soc., 46, 106. (1886MNRAS..46..106G)
Gore, J.E. 1887, Mon. Not. R. astr. Soc., 47, 268. (1887MNRAS..47..268G)
Gore, J.E. 1888, Mon. Not. R. astr. Soc., 48, 265. (1888MNRAS..48..265G)
Gore, J.E. 1890, Mon. Not. R. astr. Soc., 50, 318. (1890MNRAS..50..318G)
Gore, J.E. 1891, Mon. Not. R. astr. Soc., 51, 334. (1891MNRAS..51..334G)
Gotz, P. 1906, Publ. astr. Inst. Konigstuhl-Heidelberg, 2, No., 4.
Grassberger, W.H. and Herbig, G.H. 1952, Pub. Astr. Soc. Pacific, 64, 28. (1952PASP...64...28G)
Griffin, R.F. 1982, private communication.
Groeneveld, I. 1944, Veroff. astr. Rechen Inst. Heidelberg, 14, No. 5.
Guetter, H.H. and Hewitt, A.V. 1984, Inf. Bull. Var. Stars, No., 2499 (IBVS N°.2499)
Gunther, O. 1939, Z. f. Astrophys., 18, 212.
Gur'yev, N. 1937, Tadjik Cirk., No. 28, 2.
Gur'yev, N. 1938, Tadjik Cirk., No. 35, 1.
Gussow, H. 1930, Astr. Nachr., 237, 321. (1930AN....237..321G)
Guthnick, P. 1921, Astr. Nachr., Jubilaumsnummer.
Hacke, G. 1989, Mitt. veranderl. Sterne, 11, No. 3, 194.
Hagen, J.G. 1891, Obs. Var. Stars, Georgetown Coll. Obs.
Hagen, J.G. 1903, Beob. veranderl. Sterne, Berlin.
Hall, D.S. 1990, in "Active Close Binaries", NATO ASI C319, ed. C. Ibanoglu, Kluwer, p. 95.
Hall, J.S. 1934, Astrophys. J., 79, 145. (1934ApJ....79..145H)
Harper, W.E. 1934, Publ. D.A.O. Victoria, VI, No., 10, 151.
Harper, W.E. 1937, Publ. D.A.O. Victoria, VII, No. 1, 1.
Harris, D.L. 1953, Astrophys. J., 118, 346. (1953ApJ...118..346H)
Harris, H.C. and Wallerstein, G. 1984, Astron. J., 89, 379. (1984AJ.....89..379H)
Harris, H.C. and Welch, D.L. 1989, Astron. J., 98, 981. (1989AJ.....98..981H)
Harris, H.C., Olszewski, E.W., and Wallerstein, G. 1979, Astron. J., 84, 1598. (1979AJ.....84.1598H)
Harris H.C., Welch, D.L., Kraft, R.P., and Schmidt, E.G. 1987, Astron. J., 94, 403. (1987AJ.....94..403H)
Hase, V. 1929, Pulkovo Bull., 11, 345.
Haug, U. 1970, Astron. Astrophys. Suppl., 1, 41. (1970A&AS....1...41H)
Haupl, W. 1988, Astr. Nachr., 309, 327. (1988AN....309..327H)
Haynes, E.S. 1914, Lick Obs. Bull., 8, 85.
Hellerich, J. 1925, Astr. Nachr., 225, 7. (1925AN....225....7H)
Hellerich, J. 1935, Astr. Nachr., 256, 221. (1935AN....256..221H)
Henden, A.A. 1979, Mon. Not. R. astr. Soc., 189, 149. (1979MNRAS.189..149H)
Henriksson, G. 1982, Rep. Obs. Lund., No. 18, 89.
Henroteau, F. 1924, Publ. Dominion Obs.Ottawa, 9, No. 1.
Henroteau, F. 1925, Publ. Dominion Obs.Ottawa, 9, No., 3.
Henroteau, F. 1928, Publ. Dominion Obs.Ottawa, 9, No. 5.
Henroteau, F. and Vibert-Douglas, A. 1929, ibid., 9, No., 7.
Hertzsprung, E. 1909, Astr. Nachr., 182, 289. (1909AN....182..289H)
Hertzsprung, E. 1917, Astr. Nachr., 205, 281. (1917AN....205..281H)
Hertzsprung, E. 1919, Astr. Nachr., 208, 51. (1919AN....208...51H)
Hertzsprung, E. 1922, Bull. Astr. Inst. Netherl., 1, 63.
Hoffleit, D. and Jaschek, C. 1982, The Bright Star Catalog, 4th ed., Yale Univ. Obs., New Haven.
Hopmann, J. 1926, Astr. Nachr., 227, 257. (1926AN....227..257H)
Huffer, C.M. 1928a, Publ. Washburn Obs., 15, 127.
Huffer, C.M. 1928b, Publ. Washburn Obs., 15, 132.
Huffer, C.M. 1931, Publ. Washburn Obs., 15, 205.
Imbert, M. 1983, Astron. Astrophys. Suppl., 53, 85. (1983A&AS...53...85I)
Irwin, J.B. 1961, Astrophys. J. Suppl., 6, 253. (1961ApJS....6..253I)
Jacobsen, T.S. 1926, Lick Obs. Bull., 12, 138.
Jacobsen, T.S. 1954, Publ. D.A.O. Victoria, 10, 145.
Jacobsen, T.S. 1961, Pub. Astr. Soc. Pacific, 73, 61. (1961PASP...73...61J)
Jacobsen, T.S. and Wallerstein, G. 1981, Pub. Astr. Soc. Pacific, 93, 481. (1981PASP...93..481J)
Jacobsen, T.S. and Wallerstein, G. 1982, Pub. Astr. Soc. Pacific, 94, 471. (1982PASP...94..471J)
Jacobsen, T.S. and Wallerstein, G. 1987, Pub. Astr. Soc. Pacific, 99, 138. (1987PASP...99..138J)
Janot-Pacheco, E. 1976, Astron. Astrophys. Suppl., 25, 159. (1976A&AS...25..159J)
Johansen, K.T. 1971, Astron. Astrophys., 15, 311. (1971A&A....15..311J)
Jordan, F.C. 1919, Astrophys. J., 50, 174. (1919ApJ....50..174J)
Jordan, F.C. 1929, Publ. Allegheny Obs., 7, No. 1.
Joy, A.H. 1937, Astrophys. J., 86, 363. (1937ApJ....86..363J)
Kaiser, A. 1915, Astr. Beob. Sternw. Deutschen Univ. Prag, Ser., 2, No. 2.
Kheilo, E.S. 1962, Perem. Zvezdy, 14, 131. (1962PZ.....14..131K)
Kiess, C.C. 1917, Publ. Obs. Michigan, 3, 131.
Kopff, A. 1902, Publ. astr. Inst. Konigstuhl-Heidelberg, 1 ,185.
Koshkina, L.N. 1963, Perem. Zvezdy, 14, 472. (1963PZ.....14..472K)
Kovacs, G., Kisvarsanyi, E., and Buchler, R. 1990, Astrophys. J., 351, 606. (1990ApJ...351..606K)
Kovacs, G. and Szabados, L. 1979, Inf. Bull. Var. Stars, No. 1719. (IBVS N°.1719)
Kox, H. 1935, Astr. Nachr., 256, 21. (1935AN....256...21K)
Krebs, C. 1935, Astr. Nachr., 257, 113. (1935AN....257..113K)
Krebs, C. 1936, Astr. Nachr., 261, 109. (1936AN....261..109K)
Kristensen, J.A. 1923, Astr. Nachr., 218, 87. (1923AN....218...87K)
Kristensen, J.A. 1924, Astr. Nachr., 220, 257. (1924AN....220..257K)
Kristensen, J.A. 1926, Astr. Nachr., 228, 35. (1926AN....228...35K)
Kukarkin, B.V. 1940, Trudy gos. astr. Inst. Sternberga, 13, 1.
Kukarkina, N.P. 1954, Perem. Zvezdy, 10, 92. (1954PZ.....10...92K)
Kukarkina, N.P. 1955, Perem. Zvezdy, 10, 323. (1955PZ.....10..323K)
Kulikov, V.I. 1957, Perem. Zvezdy, 11, 472. (1957PZ.....11..472K)
Kun, M. 1986, Astrophys. Space Sci. 125, 13. (1986Ap&SS.125...13K)
Kun, M. and Szabados, L. 1988, Inf. Bull. Var. Stars, No., 3241. (IBVS N°.3241)
Kurochkin, N.E. 1966, Perem. Zvezdy 16, 10. (1966PZ.....16...10K)
Kwee, K.K. and Braun, L.D. 1967, Bull Astr. Inst. Netherl., Suppl., 2, 77.
Lacchini, G.B. 1921, Astr. Nachr., 214, 149. (1921AN....214..149L)
Landis, H.J. 1973, J.A.A.V.S.O., 1, No. 1, 38.
Landis, H.J. 1976, J.A.A.V.S.O., 4, No. 2, 84.
Latyshev, I.N. 1969, Perem. Zvezdy, 17, 64. (1969PZ.....17...64L)
Lau, H.E. 1904, B.S.A.F., 18, 237.
Lau, H.E. 1907 B.S.A.F., 21, 92.
Leiner, E. 1922, Astr. Nachr., 215, 421. (1922AN....215..421L)
Leiner, E. 1924, Astr. Nachr., 221, 137. (1924AN....221..137L)
Leiner, E. 1926, Astr. Nachr., 227, 103. (1926AN....227..103L)
Leiner, E. 1928, Astr. Nachr., 233, 323. (1928AN....233..323L)
Leiner, E. 1929, Astr. Nachr., 235, 267. (1929AN....235..267L)
Leiner, E. 1938, Astr. Nachr., 267, 3. (1938AN....267....3L)
Leonard, P.J.T. and Turner, D.G. 1986, J. R. astr. Soc. Canada, 80, 240.
Liau, S.-P. 1935, Publ. Obs. Lyon, 1, No. 13.
Lloyd Evans, T. 1968, Mon. Not. R. astr. Soc. 141, 109. (1968MNRAS.141..109L)
Lloyd Evans, T. 1980, S.A.A.O. Circ. 1, No., 5, 257.
Lloyd Evans, T. 1984, Observatory, 104, 26. (1984Obs...104...26L)
Lohnert, K. 1909, Publ. astr. Inst. Konigstuhl-Heidelberg, 3, No., 6.
Luizet, M. 1899, Astr. Nachr., 149, 316. (1899AN....149..316L)
Luizet, M. 1907, Astr. Nachr., 175, 309. (1907AN....175..309L)
Luyten, W.J. 1922, Ann. Sterrew. Leiden, 13 No. 2.
Lust-Kulka R. 1954, Z. f. Astrophys., 33 211.
Madore, B.F. 1977, Mon. Not. R. astr. Soc., 178, 505. (1977MNRAS.178..505M)
Madore, B.F. and Fernie, J.D. 1980, Pub. Astr. Soc. Pacific, 92, 315. (1980PASP...92..315M)
Mahmoud, F. and Szabados, L. 1980, Inf. Bull. Var. Stars, No. 1895. (IBVS N°.1895)
Mandel', O.E. 1970 Perem. Zvezdy, 17, 347.
Makarenko, E.N. 1969, Perem. Zvezdy, 17, 31. (1969PZ.....17...31M)
Malik G.M. 1965, Astron. J., 70, 94. (1965AJ.....70...94M)
Mariska, J.T., Doschek, G.A., and Feldman, U. 1980, Astrophys. J., 238, L87. (1980ApJ...238L..87M)
Markwick, E.E. 1892, Mem. B.A.A., 1, 71.
Martin, C. and Plummer, H.C. 1916, Mon. Not. R. astr. Soc., 76, 240. (1916MNRAS..76..240M)
Martin, C. and Plummer, H.C. 1919, Mon. Not. R. astr. Soc., 80, 33. (1919MNRAS..80...33M)
Martynov, D.Ya. 1951, Publ. Engelhardt Obs., No., 26.
Mayall, M.W. 1964, A.A.V.S.O. Q. Rep., No., 26.
McAlister, H.A. and Hartkopf, W.I. 1988, CHARA Contr., Atlanta, No. 2.
McNamara D.H. and Chapman, R. 1977, Pub. Astr. Soc. Pacific, 89, 329. (1977PASP...89..329M)
Mergentaler, J. 1948, Wroclaw Contr., No. 1, 7.
Mermilliod J.-C. Mayor, M., and Burki, G. 1987, Astron. Astrophys. Suppl., 70, 389. (1987A&AS...70..389M)
Meshkova, T.S. 1940, Perem. Zvezdy, 5, 255. (1940PZ......5..255M)
Metzger, M.R., Caldwell, J.A.R., McCarthy, J.K., and Schechter, P.L. 1990, S.A.A.O. Preprint, No., 683.
Meyers, C.J.E. 1988, J.A.A.V.S.O., 17, 15.
Miller, J. and Preston, G. 1964a, Pub. Astr. Soc. Pacific., 76, 47. (1964PASP...76...47M)
Miller, J. and Preston, G. 1964b, Astrophys. J., 139, 1126. (1964ApJ...139.1126M)
Millis, R.L. 1969, Lowell Obs. Bull., No. 148.
Milone, E.F. 1970, Inf. Bull. Var. Stars, No., 482. (IBVS N°.482)
Mitchell, R.I., Iriarte, B., Steinmetz, D., and Johnson, H.L. 1964, Bol. Obs. Tonantzintla y Tacubaya, 3, No., 24.
Moffett, T.J. and Barnes, T.G. III 1984, Astrophys. J. Suppl., 55, 389. (1984ApJS...55..389M)
Moffett, T.J. and Barnes, T.G. III 1987, Pub. Astr. Soc. Pacific, 99, 1206. (1987PASP...99.1206M)
Moncibowitz, A. 1938, Contr. Lvov Obs., No., 9.
Muller, G. and Kempf, P. 1897, Astr. Nschr., 146, 40.
Mundler, M. 1911, Veroff. astr. Rechen Inst. Heidelberg, 6, No. 5.
Nassau, J.J. and Ashbrook, J. 1942, Astron. J., 50, 66. (1942AJ.....50...66N)
Nielsen, A.V. 1927a, Astr. Nachr., 229, 109. (1927AN....229..109N)
Nielsen, A.V. 1927b, Astr. Nachr., 229, 283. (1927AN....229..283N)
Nielsen, A.V. 1927c, Astr. Nachr., 231, 113. (1927AN....231..113N)
Nielsen, A.V. 1941, Medd. Ole Romer Obs., Aarhus, No. 16 ,205.
Nielsen, A.V. 1954, Medd. Ole Romer Obs., Aarhus, No., 24 ,337.
Nijland, A.A. 1923, Utrecht Rech., 8.
Nikulina, T.G. 1959, Byull. Inst. Astrofiz. Dushanbe, No. 25, 31.
Niva G.D. and Schmidt, E.G. 1979, Astrophys. J., 234, 245. (1979ApJ...234..245N)
Novikov, I.D. 1951, Perem. Zvezdy, 8, 248. (1951PZ......8..248N)
Oke, J.B. 1961, Astrophys. J., 133, 90. (1961ApJ...133...90O)
Olivier, C.P. 1952, Publ. Univ. Pa, Astr. Ser., 7, part 2.
Oosterhoff, P.T. 1960, Bull. Astr. Inst. Netherl., 15, 199.
Opolski, A. 1948, Contr. Wroclaw Astr. Obs., No. 5.
Parenago, P.P. 1938, Trudy gos. astr. Inst. Sternberga, 12, 1.
Parenago, P.P. 1940, Perem. Zvezdy, 5, 280. (1940PZ......5..280P)
Parsons, S.B. 1983, Astrophys. J. Suppl., 53, 553. (1983ApJS...53..553P)
Parsons S.B. and Montemayor, T.J. 1982, Astrophys. J. Suppl., 49, 175. (1982ApJS...49..175P)
Pel, J.W. 1976, Astron. Astrophys. Suppl., 24, 413. (1976A&AS...24..413P)
Pel, J.W. 1978, Astron. Astrophys., 62, 75. (1978A&A....62...75P)
Percy, J.R. 1975, Inf. Bull. Var. Stars, No., 983. (IBVS N°.983)
Percy, J.R., Baskerville, I., and Trevorrow, D.W. 1979, Pub. Astr. Soc. Pacific, 91, 368. (1979PASP...91..368P)
Petrie, R.M. 1932, Publ. Obs. Michigan, 5, No., 3.
Pettit, E. and Nicholson, S.B. 1933, Astrophys. J., 78, 320. (1933ApJ....78..320P)
Pickering, E.C. 1904, Harvard Obs. Ann., 46, part 2.
Plassmann, J. 1900, Beob. veranderl. Sterne, Munster, H. 5.
Plassmann, J. 1901, Beob. veranderl. Sterne, Munster, H. 6.
Plassmann, J. 1908, Beob. veranderl. Sterne, Munster, H. 9.
Platais, I. and Shugarov, S. 1981, Inf. Bull. Var. Stars, No. 1982. (IBVS N°.1982)
Prittwitz, F. 1901, Astr. Nachr., 154, 399. (1901AN....154..399P)
Prokof'yeva, V.V. 1961, Izv. Krym. astrofiz. Obs., 25,3.
Puchinskas, A. 1962, Vilnius Biul., No., 4.
Rabe, W. 1923, Astr. Nachr., 219, 125. (1923AN....219..125R)
Redman, R.0. 1930, Publ. D.A.O. Victoria, 4, 325.
Reed, G.F. 1968, Inf. Bull. Var. Stars, No. 285. (IBVS N°.285)
Rhode, K.L. 1990a, J.A.A.V.S.O., 18, No. 2, 119.
Rhode, K.L. 1990b, J.A.A.V.S.O., 18, No. 2, 122.
Ridgway, S.T., Jacoby, G.H., Joyce, R.R., Siegel, M.J., and Wells, D.C. 1982, Astron. J., 87, 680. (1982AJ.....87..680R)
Romano, G. 1951, Pubbl. Oss. Astr. Trieste, No. 247.
Romano, G. 1955, Mem. Soc. astr. It., 26, 35. (1955MmSAI..26...35R)
Rosino, L. and Nobili, F. 1955, Pubbl. Oss. Astr. Univ. Bologna, 6, No. 15.
Rugemer, H. 1932, Astr. Nachr., 246, 209. (1932AN....246..209R)
Samus, N.N. 1990, personal communication.
Sanford, R.F. 1927, Astrophys. J., 66, 170. (1927ApJ....66..170S)
Sanford, R.F. 1928, Astrophys. J., 67, 326. (1928ApJ....67..326S)
Sanford, R.F. 1930, Astrophys. J., 72, 46. (1930ApJ....72...46S)
Sanford, R.F. 1951, Astrophys. J., 114, 331. (1951ApJ...114..331S)
Sanford, R.F. 1956, Astrophys. J., 123, 201. (1956ApJ...123..201S)
Satyvaldiev, V. 1970, Byull. Inst. Astrofiz. Dushanbe, No. 54, 21.
Scarfe, C.D. 1976, Astrophys. J., 209, 141. (1976ApJ...209..141S)
Schiller, K. 1906, Publ. astr. Inst. Konigstuhl-Heidelberg, 2, No. 8.
Schmidt, E.G. 1971, Astrophys. J., 165, 335. (1971ApJ...165..335S)
Schmidt, E.G. 1974, Mon. Not. R. astr. Soc., 167, 613. (1974MNRAS.167..613S)
Schmidt, E.G. 1976, Astrophys. J., 203, 466. (1976ApJ...203..466S)
Schmidt, E.G. and Parsons, S.B. 1982, Astrophys. J. Suppl., 48, 185. (1982ApJS...48..185S)
Schneller, H. 1936, Kl. Veroff. Berlin-Babelsberg, No. 17, 28.
Schroder, R. 1978, A.G. Mitt., No. 4, 295.
Seares, F.H. 1906, Laws Obs. Bull., No. 8.
Seares, F.H. 1907, Laws Obs. Bull., No. 13.
Shajn, G. and Albitzky, V. 1932, Mon. Not. R. astr. Soc., 92, 771. (1932MNRAS..92..771S)
Shteiman, G.S. 1958, Perem. Zvezdy, 12, 337. (1958PZ.....12..337S)
Slovak, M.H. and Barnes, T.G. III 1987, Bull. Am. Astr. Soc., 19, 753.
Slovak, M.H., Barnes, T.G. III, Evans, N.R., Welch, D.L., and Moffett, T.J. 1989, in: "The Use of Pulsating Stars in the Fundamental Problems of Astronomy", Proc. IAU Coll. No. 111, ed. E.G. Schmidt, Cambridge Univ. Press, Cambridge, p. 284.
Solov'yov, A.V. 1946, Perem. Zvezdy, 6, 38. (1946PZ......6...38S)
Solov'yov, A.V. 1952, Perem. Zvezdy, 9, 115. (1952PZ......9..115S)
Solov'yov, A.V. 1956, Stalinabad Bull., No. 16, 25.
Solov'yov, A.V. 1957, Stalinabad Bull., No. 19.
Solov'yov, A.V. 1958, Stalinabad Bull., No. 24, 22.
Solov'yov, A.V. 1959, Stalinabad Bull., No. 28, 5.
Spencer Jones, H. 1928, Cape Ann., 10, part 8, 95.
Stebbins, J., Kron, G.E. and Smith, J.L. 1952, Astrophys. J., 115, 292. (1952ApJ...115..292S)
Stobie, R.S. and Balona, L.A. 1979, Mon. Not. R. astr. Soc., 189, 641. (1979MNRAS.189..641S)
Struve, O., 1945, Astrophys. J., 102, 232. (1945ApJ...102..232S)
Sudzius, J. 1969, Bull. astr. Obs. Vilnius, No. 26.
Svolopoulos, S. 1960, Astron. J., 65, 473. (1960AJ.....65..473S)
Szabados, L. 1977, Mitt. Sternw. ung. Akad. Wiss., Budapest, No. 70. (Paper I). CoKon70;
Szabados, L. 1980, Mitt. Sternw. ung. Akad. Wiss., Budapest, No. 76. (Paper II). CoKon76;
Szabados, L. 1981, Commun. Konkoly Obs. Hung. Acad. Sci., Budapest, No. 77. (Paper III). CoKon77;
Szabados, L. 1983, Astrophys. Space Sci., 96, 185. (1983Ap&SS..96..185S)
Szabados, L. 1989, Commun. Konkoly Obs. Hung. Acad. Sci., Budapest, No. 94. (Paper IV). CoKon94;
Szabados, L. 1990a, Mon. Not. R. astr. Soc., 242, 285. (1990MNRAS.242..285S)
Szabados, L. 1990b, Sonneberg Veroff., 10, 5, 395.
Takase, B. 1969, Tokyo Astr. Bull., 2nd Ser., No. 191.
Tass, A. 1925, Publ. ung. Astrophys. Obs., Budapest, 2.
Teplitskaya, R.B. 1951, Perem. Zvezdy, 8, 215. (1951PZ......8..215T)
Terkan, L. 1935, Astr. Nachr., 257, 121. (1935AN....257..121T)
Trammell, S.R. 1987, J.A.A.V.S.O., 16, No. 2, 104.
Turner, D.G. 1978, J. R. astr. Soc. Canada, 72, 248.
Turner, D.G. 1980, Astrophys. J., 235, 146. (1980ApJ...235..146T)
Usenko, I.A. 1990a, Inf. Bull. Var. Stars, No. 3519. (IBVS N°.3519)
Usenko, I.A. 1990b, Kinematika i Fizika Nebesnych Tel, 6, No. 3, 91.
Valentiner, W. 1900, Veroff. astr. Rechen Inst. Heidelberg, I.
van der Bilt, J. 1925, J. Observateurs, 8, 57.
van der Bilt, J. 1926a, J. Observateurs, 9, 1.
van der Bilt, J. 1926b, J. Observateurs, 9, 23.
Vasil'yanovskaya, O.P. 1977, Perem. Zvezdy, 20, 467. (1977PZ.....20..467V)
Visvanathan, N. 1989, Astrophys. J., 346, 629. (1989ApJ...346..629V)
Vyskupaitis, V. 1961, Vilnius Biul., No. 3, 21.
Wachmann, A.A. 1935, Astr. Nachr., 255, 351. (1935AN....255..351W)
Wachmann, A.A. 1976, Astron. Astrophys. Suppl., 23, 249. (1976A&AS...23..249W)
Wallerstein, G. 1972, Pub. Astr. Soc. Pacific, 84, 656. (1972PASP...84..656W)
Wallerstein, G. 1983, Pub. Astr. Soc. Pacific, 95, 422. (1983PASP...95..422W)
Wallerstein, G. 1987, personal communication.
Walker, A.D. 1921, Pop. Astr., 29, 429, 501, 576, 646.
Walker, A.D. 1922, Pop. Astr., 30, 45, 118, 178.
Walker, A.R. 1987, S.A.A.O. Circ., No. 11, 131.
Walraven, J.H., Tinbergen, J., and Walraven, Th. 1964, Bull. astr. Inst. Netherl., 17, 520.
Walraven, Th., Muller, A.B., and Oosterhoff, P.Th. 1958, Bull. astr. Inst. Netherl., 14, 81.
Walter, K. 1943, Astr. Nachr., 273, 277. (1943AN....273..277W)
Wamsteker, W. 1972, Inf. Bull. Var. Stars, No. 690. (IBVS N°.690)
Weaver, H.F., Steinmetz, D., and Mitchell, R.I. 1960, Lowell Obs. Bull., 5, 30.
Welch, D.L. and Evans, N.R. 1989, Astron. J., 97, 1153. (1989AJ.....97.1153W)
Welch, D.L., Wieland, F., McAlary, C.W., McGonegal, R., Madore, B.F., McLaren, R.A., and Neugebauer, G. 1984, Astrophys. J. Suppl., 54, 547. (1984ApJS...54..547W)
Wendell, O.C. 1913, Harvard Obs. Ann., 69.
Wilkens, A. 1906, Astr. Nachr., 172, 305. (1906AN....172..305W)
Williams, A.S. 1900, Astr. Nachr., 152, 77. (1900AN....152...77W)
Williams, J.A. 1966, Astron. J., 71, 615. (1966AJ.....71..615W)
Wilson, T.D., Carter, M.W., Barnes, T.G. III, van Citters, G.W., and Moffett, T.J. 1989, Astrophys. J. Suppl., 69, 951. (1989ApJS...69..951W)
Winzer, J.E. 1973, Astron. J., 78, 618. (1973AJ.....78..618W)
Wirtz, C.W. 1901, Astr. Nachr., 154, 317. (1901AN....154..317W)
Wisniewski, W.Z. and Johnson, H.L. 1968, Commun. lunar planet. Lab., 7, No. 112.
Wright, W.H. 1899, Astrophys. J., 9, 59. (1899ApJ.....9...59W)
Wylie, C.C. 1922, Astrophys. J., 56, 217. (1922ApJ....56..217W)
Young, R.K. 1939, Publ. David Dunlap Obs., 1,71.
Zakharov, G.P. 1924a, Astr. Nachr., 221, 133. (1924AN....221..133Z)
Zakharov, G.P. 1924b, Astr. Nachr., 222, 293. (1924AN....222..293Z)
Zakharov, G.P. 1928, Tashkent Publ., 1, 74.
Zakharov, G.P. 1954, Perem. Zvezdy, 10, 79. (1954PZ.....10...79Z)
Zeipel, H. von 1908, Astr. Nachr., 177, 369. (1908AN....177..369Z)
Zinner, E. 1932, Veroff. Remeis-Sternw. aroberg, 1, H. 3.
Zinner, E. and Wachmann, A.A. 1931, ibid., 3.
Zonn, W. 1933, Wilno Bul. 1., No. 14.
Zverev, M. 1936, Trudy gos. astr. Inst. Sternberga, 8, 1.