Non-Periodic Phenomena in Variable Stars
IAU Colloquium, Budapest, 1968
PHOTOMETRIC OBSERVATIONS OF NOVA WZ SAGITTAE AND
THEIR INTERPRETATION
W. KRZEMINSKI and J. SMAK
Institute of Astronomy, Polish Academy of Sciences, Warsaw, Poland
ABSTRACT
A new model of the binary system WZ Sge is proposed, in which the secondary
component contributes about 20 percent to the total light. The W UMa-type light
curve (except for the primary eclipse) is explained as a result of the
aspherical shape of the secondary. Both components are degenerate stars.
Their effective temperatures are approximately 20000 K and 8000 K.
The binary system Nova WZ Sagittae has several unique properties and
differs much from other known close binaries. Four years ago a model of
this system was published (Krzeminski and Kraft 1964) based on
spectroscopic and photometry observations available at that time.
According to that model the masses of the components are about 0.6 m Sun
and 0.03 m Sun, giving an unusually small mass-ratio of about 0.05. The
primary, more massive component, whose stationary absorption lines of hydrogen
are observed, is a white dwarf with T_e = 13600 K and M_bol = +10.4.
The secondary is a dM star of very low luminosity and fills its
Roche limit. The primary is surrounded by a gaseous ring rotating with
the velocity of 720 km/sec. The characteristic S-wave component of the
hydrogen emission lines, which is visible on single-trail spectrograms
approximately 90 out of phase with respect to the light curve, is
attributed to a strong stream ejected from the secondary toward the
primary component. The primary eclipse consists of a partial eclipse of
the white dwarf and of covering of the rotating ring and the stream by
the dM component. The secondary eclipse (shifted to the phase 0.54) is
interpreted as an annular eclipse of the stream by the white dwarf; no
photometric effects of the eclipse fo the dM star itself are observed
since it is fainter than the primary by about 5 mag. (in V).
In 1964-1967 new photoelectric observations (in the UBV system) were
made with the 120-inch, 100-inch, and 193-cm telescopes of the Lick,
Mount Wilson, and Haute Provence observatories, respectively. Several
objections to the previous model together with the new photometric results
raised the need for revising the model. Figs. 1 and 2 show the composite light
and color curves based on new data; one can recall here that the photometric
data available prior to 1964 consisted of the ultraviolet light curves only.
The following points should be raised as being inconsistent with the previous
model: (a) the W UMa-type light curve outside of minima; in addition one may
note that the first photometric elongation (i.e. near the phase 0.25) is usually
slightly brighter than the second (i.e. the phase 0.75); (b) the new U-B color
is much different from that given by Walker (1957) and used in the previous
model; the new measurements give <(U-B)> = -0.93, and <(B-V)> = +0.10;
(c) the secondary eclipse in the V-curve is of comparable depth with
that in the B-curve; if it were due to an annular eclipse of the stream by
the white dwarf it should be almost undetectable in the yellow region where
no light from the stream (except for the Paschen continuum) could be present;
(d) the position of the secondary minimum is not constant but varies between
phases 0.50 and 0.56.
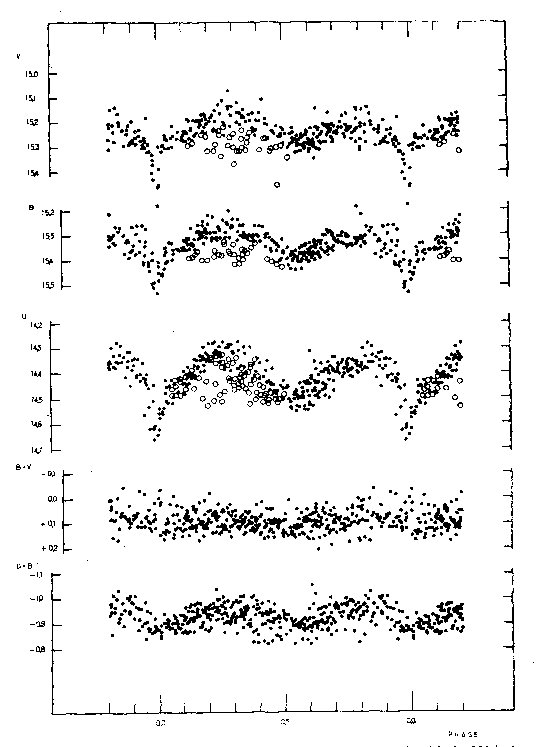 Fig. 1. Light and color curves of WZ Sge based on observations made with
the 120-inch telescope in 1964.
Fig. 1. Light and color curves of WZ Sge based on observations made with
the 120-inch telescope in 1964.
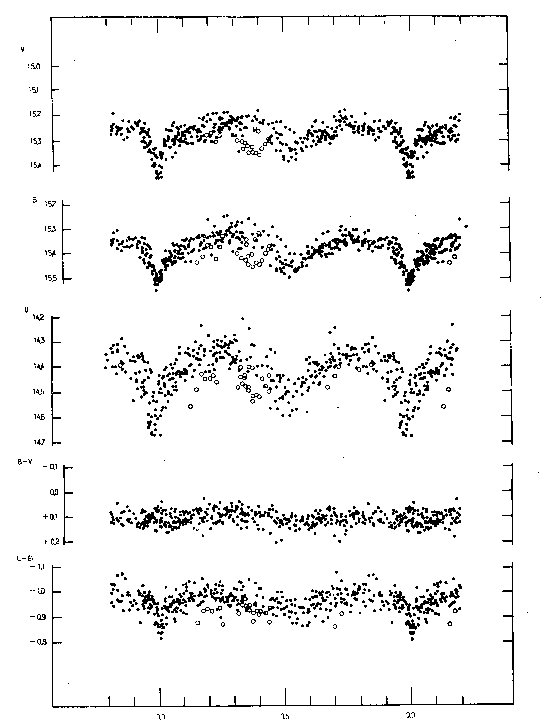 Fig. 2. Light and color curves of WZ Sge based on observations made with
the 193-cm telescope in 1964.
Our new model retains several features of the previous one (Fig. 3).
Thus we have a binary system with a very small mass-ratio and with a
very small mass of the secondary. Contrary to the original model,
however, we assume that the secondary may contribute a non-negligible
fraction of the total light of the system. Because of its non-spherical
shape and effective gravity effects it could then be made responsible
for the W UMa-type light curve. Following a suggestion by Paczynski
(1967) one can assume that the secondary is a degenerate star with an
estimated effective gravity of about log g = 7. Rucinski (1968) has
recently computed the photometric effects for a highly distorted white
dwarf secondary in a close binary system for two different mass-ratios
of 1/10 and 1/19 and for T_e = 8000 K and log g = 7. The temperature used
was simply the lowest for which the model atmosphere data were still
available (Teraschita and Matsuschima 1966). However, it will be shown
below, that the temperature of the secondary of WZ Sge is, in fact,
close to about 6500-8000 K. According to Rucinski's results the
photometric effects at lambda=5000 A consist of a nearly sinusoidal variation
of considerable amplitude: the star is about 60 per cent brighter when
seen at elongations, as compared with phases 0.0 and 0.5. The observed
mean amplitude of the W UMa-type variations of WZ Sge (in B and V),
including the secondary but excluding the deep part of the primary minimum,
amounts to about 0.1 mag. Therefore the fractional luminosity of the secondary
component should be equal to about L_2 = 0.20, in order to account for
the observed amplitude. The ratio of luminosities should be L_2/L_1 = 0.25.
Fig. 2. Light and color curves of WZ Sge based on observations made with
the 193-cm telescope in 1964.
Our new model retains several features of the previous one (Fig. 3).
Thus we have a binary system with a very small mass-ratio and with a
very small mass of the secondary. Contrary to the original model,
however, we assume that the secondary may contribute a non-negligible
fraction of the total light of the system. Because of its non-spherical
shape and effective gravity effects it could then be made responsible
for the W UMa-type light curve. Following a suggestion by Paczynski
(1967) one can assume that the secondary is a degenerate star with an
estimated effective gravity of about log g = 7. Rucinski (1968) has
recently computed the photometric effects for a highly distorted white
dwarf secondary in a close binary system for two different mass-ratios
of 1/10 and 1/19 and for T_e = 8000 K and log g = 7. The temperature used
was simply the lowest for which the model atmosphere data were still
available (Teraschita and Matsuschima 1966). However, it will be shown
below, that the temperature of the secondary of WZ Sge is, in fact,
close to about 6500-8000 K. According to Rucinski's results the
photometric effects at lambda=5000 A consist of a nearly sinusoidal variation
of considerable amplitude: the star is about 60 per cent brighter when
seen at elongations, as compared with phases 0.0 and 0.5. The observed
mean amplitude of the W UMa-type variations of WZ Sge (in B and V),
including the secondary but excluding the deep part of the primary minimum,
amounts to about 0.1 mag. Therefore the fractional luminosity of the secondary
component should be equal to about L_2 = 0.20, in order to account for
the observed amplitude. The ratio of luminosities should be L_2/L_1 = 0.25.
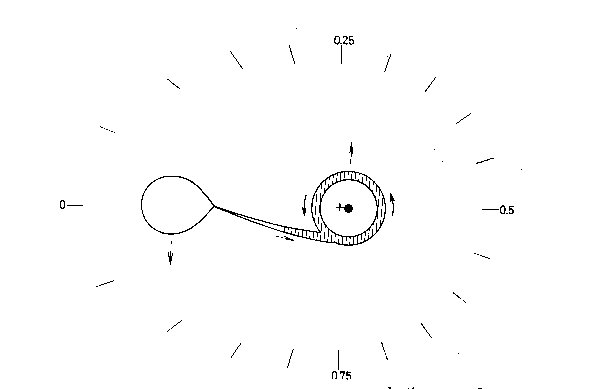 Fig. 3. Schematic model of WZ Sge. The plus sign marks the center of mass.
The observed phase shift of the secondary minimum cannot be explained
by our model. However, since the position of the secondary minimum is
not constant, one can assume that the phase shift could be due to an
extra source of light of variable intensity located on the surface of
the secondary component asymmetrically with respect to the line joining
the two components; this extra light could contribute to the light curve
between phases (approximately) 0.2-0.6, producing not only the observed
shift of the secondary minimum but also the slight excess of luminosity
at the phase 0.25. A number of mechanisms connected either with a
non-synchronous rotation or mass ejection could be responsible for the
existence of such a "hot spot".
Fig. 4 shows the observed position of WZ Sge in the two-color diagram.
Also shown is a grid of lines based on model atmospheres computed by Teraschita
and Matsuschima (1966). To obtain U-B and B-V of the primary component one has
to correct the observed colors for the effect of the hydrogen emission and for
the secondary component. Both effects were evaluated in an approximate way. In
particular, it was assumed that the ratio of luminosities (mean for B and V)
is L_2/L_1 = 0.25, as given above; and that the colors of the secondary should
be close to those of other more typical white dwarfs with T_e = 6000-8000 K
and log g = 7, i.e. should lie within the rectangle in the lower right part of
the two-color diagram (Fig. 4). It turns out that the resulting colors
of the primary are not very sensitive to these assumptions and should lie
within a small region, close to the observed point, as shown in Fig. 4.
A comparison with the theoretical data suggests the following characteristics
of the primary: T_e,1~= 18000 K, log g_1 ~= 9, provided no reddening
corrections need to be introduced. An independent estimate of these parameters
is possible via the observed profile of the H-gamma absorption line
(Greenstein 1957) and the theoretical profiles published by Teraschita and
Matsuschima (1966). Because of the emission component in the center of line
only the absorption wings could be taken into account and for that reason it
was impossible to determine T_e and g in a unique way; instead a "family" of
solutions corresponding to the different values of T_e and g was obtained.
A "locus" corresponding to these solutions is shown also in the two-color
diagram (Fig. 4). It can be seen that the colors of the primary component lie
very closely to this locus and with a very small correction for interstellar
reddening the agreement would be even better. Taking into account both sets of
data (i.e. from colors and from the H-gamma line) one can state that the
effective temperature of the primary is between 18000 K and 20000 K
(instead of 13600 K in the original model) and its surface gravity about
log g = 8.5. The value of log g, together with the theoretical mass-radius
relation for white dwarfs would imply that the mass of the primary should be
larger than 1 solar mass, i.e. much larger than that obtained by Krzeminski and
Kraft (1964) within the previous model. It is clear, however, that the
accuracy of this determination is quite low.
Fig. 3. Schematic model of WZ Sge. The plus sign marks the center of mass.
The observed phase shift of the secondary minimum cannot be explained
by our model. However, since the position of the secondary minimum is
not constant, one can assume that the phase shift could be due to an
extra source of light of variable intensity located on the surface of
the secondary component asymmetrically with respect to the line joining
the two components; this extra light could contribute to the light curve
between phases (approximately) 0.2-0.6, producing not only the observed
shift of the secondary minimum but also the slight excess of luminosity
at the phase 0.25. A number of mechanisms connected either with a
non-synchronous rotation or mass ejection could be responsible for the
existence of such a "hot spot".
Fig. 4 shows the observed position of WZ Sge in the two-color diagram.
Also shown is a grid of lines based on model atmospheres computed by Teraschita
and Matsuschima (1966). To obtain U-B and B-V of the primary component one has
to correct the observed colors for the effect of the hydrogen emission and for
the secondary component. Both effects were evaluated in an approximate way. In
particular, it was assumed that the ratio of luminosities (mean for B and V)
is L_2/L_1 = 0.25, as given above; and that the colors of the secondary should
be close to those of other more typical white dwarfs with T_e = 6000-8000 K
and log g = 7, i.e. should lie within the rectangle in the lower right part of
the two-color diagram (Fig. 4). It turns out that the resulting colors
of the primary are not very sensitive to these assumptions and should lie
within a small region, close to the observed point, as shown in Fig. 4.
A comparison with the theoretical data suggests the following characteristics
of the primary: T_e,1~= 18000 K, log g_1 ~= 9, provided no reddening
corrections need to be introduced. An independent estimate of these parameters
is possible via the observed profile of the H-gamma absorption line
(Greenstein 1957) and the theoretical profiles published by Teraschita and
Matsuschima (1966). Because of the emission component in the center of line
only the absorption wings could be taken into account and for that reason it
was impossible to determine T_e and g in a unique way; instead a "family" of
solutions corresponding to the different values of T_e and g was obtained.
A "locus" corresponding to these solutions is shown also in the two-color
diagram (Fig. 4). It can be seen that the colors of the primary component lie
very closely to this locus and with a very small correction for interstellar
reddening the agreement would be even better. Taking into account both sets of
data (i.e. from colors and from the H-gamma line) one can state that the
effective temperature of the primary is between 18000 K and 20000 K
(instead of 13600 K in the original model) and its surface gravity about
log g = 8.5. The value of log g, together with the theoretical mass-radius
relation for white dwarfs would imply that the mass of the primary should be
larger than 1 solar mass, i.e. much larger than that obtained by Krzeminski and
Kraft (1964) within the previous model. It is clear, however, that the
accuracy of this determination is quite low.
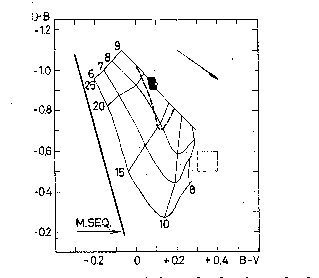 Fig. 4. The two-color diagram. An open circle marks the observed colors
of WZ Sge A rectangle in the lower right part of the diagram is assumed
to contain the colors of the secondary component. The colors of the
primary should lie in the hatched area located near the observed point. A grid
of lines is based on model atmospheres (Teraschita and Matsuschima 1966) with
T_e = 8000, 10000, 15000, 20000, and 25000 K, and log g = 6, 7, 8, and 9.
Finally, the broken line is the "locus" based on the H-gamma absorption
profile belonging to the primary component.
Finally one can estimate the effective temperature of the secondary
component. The ratio of luminosities, which is known (see above), can be
written down as a function of radii and effective temperatures of the
components. By using the mass-radius relation one can replace the radii
with masses. With T_e,1 known (approximately, see above) one can compute
T_e,2 as a function of various combinations of M_1 and M_2. Such
computations were made with M_1 = 0.4-1.4 M_Sun and M_2 = 0.02-0.06 M_Sun.
The resulting values of T_e,2, lie in the range 6500-8000 K.
Therefore the secondary turns out to be much hotter than in the original
model; its evolutionary significance remains, however, equally obscure.
The results presented above are of preliminary character and form only a
part of our rediscussion of WZ Sge. The second part, now under way, will
deal with the dynamical properties of the system. Final results will be
published in "Acta Astronomica".
REFERENCES
Greenstein, J. L., 1957, Astrophys. J., 126, 23.
Krzeminski, W., Kraft, R. P., 1964, Astrophys. J., 140, 921.
Paczynski, B., 1967, Acta Astr., 17, 287.
Rucinski, S. M., 1968, This Colloquium. CoKon 65-47
Teraschita, Y., Matsuschima, S., 1966, Astrophys. J. Suppl, 13, 461.
Walker, M. F., 1957, I. A. U. Symposium No. 3, Ed. G. H. Herbig (Cambridge,
Cambridge University Press), p. 46.
Fig. 4. The two-color diagram. An open circle marks the observed colors
of WZ Sge A rectangle in the lower right part of the diagram is assumed
to contain the colors of the secondary component. The colors of the
primary should lie in the hatched area located near the observed point. A grid
of lines is based on model atmospheres (Teraschita and Matsuschima 1966) with
T_e = 8000, 10000, 15000, 20000, and 25000 K, and log g = 6, 7, 8, and 9.
Finally, the broken line is the "locus" based on the H-gamma absorption
profile belonging to the primary component.
Finally one can estimate the effective temperature of the secondary
component. The ratio of luminosities, which is known (see above), can be
written down as a function of radii and effective temperatures of the
components. By using the mass-radius relation one can replace the radii
with masses. With T_e,1 known (approximately, see above) one can compute
T_e,2 as a function of various combinations of M_1 and M_2. Such
computations were made with M_1 = 0.4-1.4 M_Sun and M_2 = 0.02-0.06 M_Sun.
The resulting values of T_e,2, lie in the range 6500-8000 K.
Therefore the secondary turns out to be much hotter than in the original
model; its evolutionary significance remains, however, equally obscure.
The results presented above are of preliminary character and form only a
part of our rediscussion of WZ Sge. The second part, now under way, will
deal with the dynamical properties of the system. Final results will be
published in "Acta Astronomica".
REFERENCES
Greenstein, J. L., 1957, Astrophys. J., 126, 23.
Krzeminski, W., Kraft, R. P., 1964, Astrophys. J., 140, 921.
Paczynski, B., 1967, Acta Astr., 17, 287.
Rucinski, S. M., 1968, This Colloquium. CoKon 65-47
Teraschita, Y., Matsuschima, S., 1966, Astrophys. J. Suppl, 13, 461.
Walker, M. F., 1957, I. A. U. Symposium No. 3, Ed. G. H. Herbig (Cambridge,
Cambridge University Press), p. 46.
 Fig. 1. Light and color curves of WZ Sge based on observations made with
the 120-inch telescope in 1964.
Fig. 1. Light and color curves of WZ Sge based on observations made with
the 120-inch telescope in 1964.
 Fig. 2. Light and color curves of WZ Sge based on observations made with
the 193-cm telescope in 1964.
Our new model retains several features of the previous one (Fig. 3).
Thus we have a binary system with a very small mass-ratio and with a
very small mass of the secondary. Contrary to the original model,
however, we assume that the secondary may contribute a non-negligible
fraction of the total light of the system. Because of its non-spherical
shape and effective gravity effects it could then be made responsible
for the W UMa-type light curve. Following a suggestion by Paczynski
(1967) one can assume that the secondary is a degenerate star with an
estimated effective gravity of about log g = 7. Rucinski (1968) has
recently computed the photometric effects for a highly distorted white
dwarf secondary in a close binary system for two different mass-ratios
of 1/10 and 1/19 and for T_e = 8000 K and log g = 7. The temperature used
was simply the lowest for which the model atmosphere data were still
available (Teraschita and Matsuschima 1966). However, it will be shown
below, that the temperature of the secondary of WZ Sge is, in fact,
close to about 6500-8000 K. According to Rucinski's results the
photometric effects at lambda=5000 A consist of a nearly sinusoidal variation
of considerable amplitude: the star is about 60 per cent brighter when
seen at elongations, as compared with phases 0.0 and 0.5. The observed
mean amplitude of the W UMa-type variations of WZ Sge (in B and V),
including the secondary but excluding the deep part of the primary minimum,
amounts to about 0.1 mag. Therefore the fractional luminosity of the secondary
component should be equal to about L_2 = 0.20, in order to account for
the observed amplitude. The ratio of luminosities should be L_2/L_1 = 0.25.
Fig. 2. Light and color curves of WZ Sge based on observations made with
the 193-cm telescope in 1964.
Our new model retains several features of the previous one (Fig. 3).
Thus we have a binary system with a very small mass-ratio and with a
very small mass of the secondary. Contrary to the original model,
however, we assume that the secondary may contribute a non-negligible
fraction of the total light of the system. Because of its non-spherical
shape and effective gravity effects it could then be made responsible
for the W UMa-type light curve. Following a suggestion by Paczynski
(1967) one can assume that the secondary is a degenerate star with an
estimated effective gravity of about log g = 7. Rucinski (1968) has
recently computed the photometric effects for a highly distorted white
dwarf secondary in a close binary system for two different mass-ratios
of 1/10 and 1/19 and for T_e = 8000 K and log g = 7. The temperature used
was simply the lowest for which the model atmosphere data were still
available (Teraschita and Matsuschima 1966). However, it will be shown
below, that the temperature of the secondary of WZ Sge is, in fact,
close to about 6500-8000 K. According to Rucinski's results the
photometric effects at lambda=5000 A consist of a nearly sinusoidal variation
of considerable amplitude: the star is about 60 per cent brighter when
seen at elongations, as compared with phases 0.0 and 0.5. The observed
mean amplitude of the W UMa-type variations of WZ Sge (in B and V),
including the secondary but excluding the deep part of the primary minimum,
amounts to about 0.1 mag. Therefore the fractional luminosity of the secondary
component should be equal to about L_2 = 0.20, in order to account for
the observed amplitude. The ratio of luminosities should be L_2/L_1 = 0.25.
 Fig. 3. Schematic model of WZ Sge. The plus sign marks the center of mass.
The observed phase shift of the secondary minimum cannot be explained
by our model. However, since the position of the secondary minimum is
not constant, one can assume that the phase shift could be due to an
extra source of light of variable intensity located on the surface of
the secondary component asymmetrically with respect to the line joining
the two components; this extra light could contribute to the light curve
between phases (approximately) 0.2-0.6, producing not only the observed
shift of the secondary minimum but also the slight excess of luminosity
at the phase 0.25. A number of mechanisms connected either with a
non-synchronous rotation or mass ejection could be responsible for the
existence of such a "hot spot".
Fig. 4 shows the observed position of WZ Sge in the two-color diagram.
Also shown is a grid of lines based on model atmospheres computed by Teraschita
and Matsuschima (1966). To obtain U-B and B-V of the primary component one has
to correct the observed colors for the effect of the hydrogen emission and for
the secondary component. Both effects were evaluated in an approximate way. In
particular, it was assumed that the ratio of luminosities (mean for B and V)
is L_2/L_1 = 0.25, as given above; and that the colors of the secondary should
be close to those of other more typical white dwarfs with T_e = 6000-8000 K
and log g = 7, i.e. should lie within the rectangle in the lower right part of
the two-color diagram (Fig. 4). It turns out that the resulting colors
of the primary are not very sensitive to these assumptions and should lie
within a small region, close to the observed point, as shown in Fig. 4.
A comparison with the theoretical data suggests the following characteristics
of the primary: T_e,1~= 18000 K, log g_1 ~= 9, provided no reddening
corrections need to be introduced. An independent estimate of these parameters
is possible via the observed profile of the H-gamma absorption line
(Greenstein 1957) and the theoretical profiles published by Teraschita and
Matsuschima (1966). Because of the emission component in the center of line
only the absorption wings could be taken into account and for that reason it
was impossible to determine T_e and g in a unique way; instead a "family" of
solutions corresponding to the different values of T_e and g was obtained.
A "locus" corresponding to these solutions is shown also in the two-color
diagram (Fig. 4). It can be seen that the colors of the primary component lie
very closely to this locus and with a very small correction for interstellar
reddening the agreement would be even better. Taking into account both sets of
data (i.e. from colors and from the H-gamma line) one can state that the
effective temperature of the primary is between 18000 K and 20000 K
(instead of 13600 K in the original model) and its surface gravity about
log g = 8.5. The value of log g, together with the theoretical mass-radius
relation for white dwarfs would imply that the mass of the primary should be
larger than 1 solar mass, i.e. much larger than that obtained by Krzeminski and
Kraft (1964) within the previous model. It is clear, however, that the
accuracy of this determination is quite low.
Fig. 3. Schematic model of WZ Sge. The plus sign marks the center of mass.
The observed phase shift of the secondary minimum cannot be explained
by our model. However, since the position of the secondary minimum is
not constant, one can assume that the phase shift could be due to an
extra source of light of variable intensity located on the surface of
the secondary component asymmetrically with respect to the line joining
the two components; this extra light could contribute to the light curve
between phases (approximately) 0.2-0.6, producing not only the observed
shift of the secondary minimum but also the slight excess of luminosity
at the phase 0.25. A number of mechanisms connected either with a
non-synchronous rotation or mass ejection could be responsible for the
existence of such a "hot spot".
Fig. 4 shows the observed position of WZ Sge in the two-color diagram.
Also shown is a grid of lines based on model atmospheres computed by Teraschita
and Matsuschima (1966). To obtain U-B and B-V of the primary component one has
to correct the observed colors for the effect of the hydrogen emission and for
the secondary component. Both effects were evaluated in an approximate way. In
particular, it was assumed that the ratio of luminosities (mean for B and V)
is L_2/L_1 = 0.25, as given above; and that the colors of the secondary should
be close to those of other more typical white dwarfs with T_e = 6000-8000 K
and log g = 7, i.e. should lie within the rectangle in the lower right part of
the two-color diagram (Fig. 4). It turns out that the resulting colors
of the primary are not very sensitive to these assumptions and should lie
within a small region, close to the observed point, as shown in Fig. 4.
A comparison with the theoretical data suggests the following characteristics
of the primary: T_e,1~= 18000 K, log g_1 ~= 9, provided no reddening
corrections need to be introduced. An independent estimate of these parameters
is possible via the observed profile of the H-gamma absorption line
(Greenstein 1957) and the theoretical profiles published by Teraschita and
Matsuschima (1966). Because of the emission component in the center of line
only the absorption wings could be taken into account and for that reason it
was impossible to determine T_e and g in a unique way; instead a "family" of
solutions corresponding to the different values of T_e and g was obtained.
A "locus" corresponding to these solutions is shown also in the two-color
diagram (Fig. 4). It can be seen that the colors of the primary component lie
very closely to this locus and with a very small correction for interstellar
reddening the agreement would be even better. Taking into account both sets of
data (i.e. from colors and from the H-gamma line) one can state that the
effective temperature of the primary is between 18000 K and 20000 K
(instead of 13600 K in the original model) and its surface gravity about
log g = 8.5. The value of log g, together with the theoretical mass-radius
relation for white dwarfs would imply that the mass of the primary should be
larger than 1 solar mass, i.e. much larger than that obtained by Krzeminski and
Kraft (1964) within the previous model. It is clear, however, that the
accuracy of this determination is quite low.
 Fig. 4. The two-color diagram. An open circle marks the observed colors
of WZ Sge A rectangle in the lower right part of the diagram is assumed
to contain the colors of the secondary component. The colors of the
primary should lie in the hatched area located near the observed point. A grid
of lines is based on model atmospheres (Teraschita and Matsuschima 1966) with
T_e = 8000, 10000, 15000, 20000, and 25000 K, and log g = 6, 7, 8, and 9.
Finally, the broken line is the "locus" based on the H-gamma absorption
profile belonging to the primary component.
Finally one can estimate the effective temperature of the secondary
component. The ratio of luminosities, which is known (see above), can be
written down as a function of radii and effective temperatures of the
components. By using the mass-radius relation one can replace the radii
with masses. With T_e,1 known (approximately, see above) one can compute
T_e,2 as a function of various combinations of M_1 and M_2. Such
computations were made with M_1 = 0.4-1.4 M_Sun and M_2 = 0.02-0.06 M_Sun.
The resulting values of T_e,2, lie in the range 6500-8000 K.
Therefore the secondary turns out to be much hotter than in the original
model; its evolutionary significance remains, however, equally obscure.
The results presented above are of preliminary character and form only a
part of our rediscussion of WZ Sge. The second part, now under way, will
deal with the dynamical properties of the system. Final results will be
published in "Acta Astronomica".
REFERENCES
Greenstein, J. L., 1957, Astrophys. J., 126, 23.
Krzeminski, W., Kraft, R. P., 1964, Astrophys. J., 140, 921.
Paczynski, B., 1967, Acta Astr., 17, 287.
Rucinski, S. M., 1968, This Colloquium. CoKon 65-47
Teraschita, Y., Matsuschima, S., 1966, Astrophys. J. Suppl, 13, 461.
Walker, M. F., 1957, I. A. U. Symposium No. 3, Ed. G. H. Herbig (Cambridge,
Cambridge University Press), p. 46.
Fig. 4. The two-color diagram. An open circle marks the observed colors
of WZ Sge A rectangle in the lower right part of the diagram is assumed
to contain the colors of the secondary component. The colors of the
primary should lie in the hatched area located near the observed point. A grid
of lines is based on model atmospheres (Teraschita and Matsuschima 1966) with
T_e = 8000, 10000, 15000, 20000, and 25000 K, and log g = 6, 7, 8, and 9.
Finally, the broken line is the "locus" based on the H-gamma absorption
profile belonging to the primary component.
Finally one can estimate the effective temperature of the secondary
component. The ratio of luminosities, which is known (see above), can be
written down as a function of radii and effective temperatures of the
components. By using the mass-radius relation one can replace the radii
with masses. With T_e,1 known (approximately, see above) one can compute
T_e,2 as a function of various combinations of M_1 and M_2. Such
computations were made with M_1 = 0.4-1.4 M_Sun and M_2 = 0.02-0.06 M_Sun.
The resulting values of T_e,2, lie in the range 6500-8000 K.
Therefore the secondary turns out to be much hotter than in the original
model; its evolutionary significance remains, however, equally obscure.
The results presented above are of preliminary character and form only a
part of our rediscussion of WZ Sge. The second part, now under way, will
deal with the dynamical properties of the system. Final results will be
published in "Acta Astronomica".
REFERENCES
Greenstein, J. L., 1957, Astrophys. J., 126, 23.
Krzeminski, W., Kraft, R. P., 1964, Astrophys. J., 140, 921.
Paczynski, B., 1967, Acta Astr., 17, 287.
Rucinski, S. M., 1968, This Colloquium. CoKon 65-47
Teraschita, Y., Matsuschima, S., 1966, Astrophys. J. Suppl, 13, 461.
Walker, M. F., 1957, I. A. U. Symposium No. 3, Ed. G. H. Herbig (Cambridge,
Cambridge University Press), p. 46.